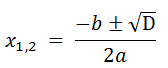Класс квадратное уравнение java

NuarkNoir / EquationSolver.java

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

package xyz . nuark ;

import java . util . regex . Matcher ;

import java . util . regex . Pattern ;

/**

* @author Nuark

* @version 1.0

*

* Класс, который решает квадратные уравнения.

* Уравнения должны поступать в формате «ax^2 + bx + c = 0″(можно и без пробелов).

* Аргументы a, b и c не должны выходить за рамки double

* double — 64-разрядное число в формате IEEE 754 с плавающей точкой [-1.7E+308 .. 1.7E+308]

*/

public class EquationSolver

public String equation ;

private double a , b , c ;

private final String regex = «([+-]? \\ d+|[+-])?x \\ ^2[ \\ s]([+-][ \\ s]? \\ d+|[+-])?x[ \\ s]+([+-] \\ s? \\ d+)[ \\ s]=[ \\ s]([+-]? \\ d+)» ;

private Pattern pattern ;

private Matcher matcher ;

public EquationSolver ( String equation ) throws Exception

equation = formatString ( equation );

if ( checkEquation ( equation ))

if (! equation . contains ( «x^2» ) || ! equation . contains ( «x» ))

throw new Exception ( «Quadratic equation expected, linear given» );

this . equation = equation ;

splitToPieces ();

> else throw new Exception ( «Not an equation» );

>

private boolean checkEquation ( String equation )

pattern = Pattern . compile ( regex );

matcher = pattern . matcher ( equation );

return matcher . find ();

>

private String formatString ( String equation )

return equation . replace ( » » , «» ). replace ( «-0» , «0» ). replace ( «=» , » = » ). replace ( «+» , » +» ). replace ( «-» , » -» ). trim ();

>

private void splitToPieces ()

String eq = this . equation ;

String [] tmp = eq . split ( » = » );

int exc = Integer . parseInt ( tmp [ 1 ]);

String [] t = tmp [ 0 ]. split ( » » );

String _a = t [ 0 ]. replace ( «x^2» , «» );

String _b = t [ 1 ]. replace ( «x» , «» );

String _c = t [ 2 ];

if (( _a . length () == 1 ) && ( «-» . equals ( _a ) || «+» . equals ( _a ))) _a = _a . concat ( «1» );

else if ( _a . length () == 0 ) _a = _a . concat ( «1» );

if (( _b . length () == 1 ) && ( «-» . equals ( _b ) || «+» . equals ( _b ))) _b = _b . concat ( «1» );

else if ( _b . length () == 0 ) _b = _b . concat ( «1» );

if (( _c . length () == 1 || _c . length () == 0 ) && ( «-» . equals ( _c ) || «+» . equals ( _c ))) _c = _c . concat ( «1» );

else if ( _c . length () == 0 ) _c = _c . concat ( «1» );

a = Double . parseDouble ( _a );

b = Double . parseDouble ( _b );

c = Double . parseDouble ( _c ) + exc ;

>

public double [] solveEquation () throws Exception

double _a = this . a ;

double _b = this . b ;

double _c = this . c ;

double discr = ( _b * _b ) — ( 4 * _a * _c );

if ( discr > 0 )

double sq_discr = Math . sqrt ( discr );

double x1 = ( _b * — 1 ) + sq_discr / ( 2 * _a );

double x2 = ( _b * — 1 ) — sq_discr / ( 2 * _a );

return new double []< x1 , x2 >;

> else if ( discr == 0 )

double x1 = ( _b * — 1 ) / ( 2 * _a );

return new double []< x1 >;

> else

throw new Exception ( «Complex number can not be expressed with double type» );

>

>

>

This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters. Learn more about bidirectional Unicode characters

package xyz . nuark ;

public class Main

public static void main ( String [] args )

String test = «4×2-4x-42=0 \n » +

«-1x^2 -2x +4 = 0 \n » +

«x^2 +0x -16 = 0 \n » +

«-x^2 +0x -16 = 0 \n » +

«x^2 +x -16 = 0 \n » +

«-x^2 +x -16 = 0 \n » +

«x^2 -x -16 = 0 \n » +

«-x^2 -x -16 = 0 \n » +

«4x^2 +0x -16 = 0 \n » +

«-0x^2 -25x +4225 = 0 \n » +

«9x^2 — 30 = 0 \n » +

«8x^2 + 45454541x — 42 = 0 \n » +

«3x^2 — 0x — 27 = 0 \n » +

«1x^2 — 0x — 16 = 0 \n » +

«25x + 50 = 0 \n » +

«123154549480 + 4 \n » +

«-25x — 50 = 0 \n » +

«1x^2 — 25x — 0 = 9 \n » +

«2x^2 — 0x — 8 = 5 \n » +

«1x^2 -0x — 16 = 0 \n » +

«3x^2 — 0x — 27 = 0 \n » +

«9x^2 — 3x + 0 = 0 \n » +

«3x^2 — 0x — 257 = 0 \n » +

«1313215645564x^2 + 6546x — 45451212115484 = 0 \n » +

«9х = 4545454 \n » +

«0 \n » +

«3x^2 — 0x + 27 = 0 \n » +

«2x^2 -1x + 28 = 0 \n » +

«1x^2 — 2x + 29 = 0 \n » +

«8x^2 a 2x + 29 = 0 \n » +

«1x^2 — 2x 1 29 = 0 \n » +

«1x^2 — 2x ++ 29 = 0 \n » +

«-2x . 29 = 0 \n » +

«-2x + 29 = 0 \n » +

«фx^2 -1x + a8 = 0» ;

for ( String eq : test . split ( » \n » ))

try

EquationSolver su = new EquationSolver ( eq );

double [] answers = su . solveEquation ();

if ( answers . length == 1 )

System . out . println ( «Equation » + eq + » has one answer: » + answers [ 0 ]);

else

System . out . println ( «Equation » + eq + » has two answers: » + answers [ 0 ] + » and » + answers [ 1 ]);

> catch ( NumberFormatException ex )

System . out . println ( «Wow, how? » + ex + » :: » + eq );

> catch ( Exception ex )

System . out . println ( ex + » :: » + eq );

>

>

>

>

Источник

Квадратное уравнение

Класс « квадратное уравнение » :
— Квадратное уравнение задается тремя числами ( a , b , c ) , которые описывают уравнения ax^2 + bx + c ;
— Существует метод для вычисления количества корней уравнения ;
— Существует метод для вычисления корней , который возвращает массив из одного или двух цифр или NULL.
Помогите пожалуйста вывести на экран корни и количество корней.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51

package ttt; public class kvadr { public static class Dannye { public int a,b,c, x1, x2; Dannye(int a, int b, int c) { this.a=a; this.b=b; this.c=c; this.x1=x1; this.x2=x2; } public void korni(double D, double x1, double x2) { D = b*b - 4*a*c; x1 = (-b + Math.sqrt(D))/2*a; x2 = (-b - Math.sqrt(D))/2*a; } public String kolichestvokorney(String s, double D) { D = b*b - 4*a*c; if (D>0) s="2 корня"; if (D==0) s="1 корень"; else s="действительных корней нету"; return s; } void show() { System.out.println("a="+a); System.out.println("b="+b); System.out.println("c="+c); System.out.println("s="+x1); } } public static void main(String[] args) { Dannye a1 = new Dannye(1,3,2); a1.show(); } }

Источник

Программирование на C, C# и Java

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Решение квадратного уравнения на Java

В этой статье рассмотрим алгоритм решения квадратного уравнения и реализуем его на языке программирования Java.

Пусть нам требуется решить уравнение вида: . Будем решать его через дискриминант. Для получения корней уравнения необходимо выполнить следующий алгоритм:

1. Вычислим дискриминант по формуле: .
2. ЕСЛИ дискриминант больше нуля, то вычислим корни уравнения x1 и x2 по формуле:

ИНАЧЕ ЕСЛИ дискриминант равен нулю, значит уравнение имеет единственный корень. Вычислим его по формуле:

ИНАЧЕ (то есть дискриминант меньше нуля) уравнение не имеет действительных корней.

Реализуем этот алгоритм на языке программирования Java.

Приступим к написанию кода программы. В начале импортируем класс Scanner, необходимый для ввода данных:

Источник

Решение квадратного уравнения

В этой статье мы рассмотрим алгоритм решения квадратного уравнение на Java.

Что такое квадратное уравнение

Квадратно уравнение – это уравнение вида:

(1)

Для вычисления значения x мы сначала вычислим дискриминант по формуле:

(2)

Далее, если значение дискриминанта больше нуля, вычислим корни уравнения по формулам:

(3)

Иначе, если дискриминант равен нулю, единственное значение x вычислим по формуле:

(4)

Иначе, если дискриминант меньше нуля, данное уравнение не имеет решения.

Реализация алгоритма решения квадратного уравнения

Вначале вычитаем исходные данные a, b и c:

Scanner scanner = new Scanner(System.in); System.out.print("Введите значение a: "); double a = scanner.nextDouble(); System.out.print("Введите значение b: "); double b = scanner.nextDouble(); System.out.print("Введите значение c: "); double c = scanner.nextDouble();

Затем вычислим дискриминант:

На основании значения дискриминанта вычислим корни уравнения, если таковые имеются:

if (d > 0) < double x1 = (-b - Math.sqrt(d)) / (2 * a); double x2 = (-b + Math.sqrt(d)) / (2 * a); System.out.println("Корни уравнения: x1 = " + x1 + ", x2 = " + x2); >else if (d == 0) < double x; x = -b / (2 * a); System.out.println("Уравнение имеет единственный корень: x = " + x); >else

Проверка

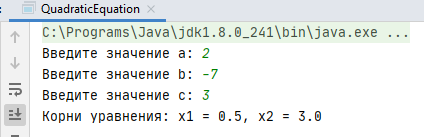
Теперь проверим программу в действии. Для следующих входных данных программа должна выдать такой результат:

(5)

Результат работы программы:

Исходный код

Полный исходный код программы:

import java.util.Scanner; public class QuadraticEquation < public static void main(String[] args) < Scanner scanner = new Scanner(System.in); System.out.print("Введите значение a: "); double a = scanner.nextDouble(); System.out.print("Введите значение b: "); double b = scanner.nextDouble(); System.out.print("Введите значение c: "); double c = scanner.nextDouble(); double d = b * b - 4 * a * c; if (d >0) < double x1 = (-b - Math.sqrt(d)) / (2 * a); double x2 = (-b + Math.sqrt(d)) / (2 * a); System.out.println("Корни уравнения: x1 = " + x1 + ", x2 = " + x2); >else if (d == 0) < double x; x = -b / (2 * a); System.out.println("Уравнение имеет единственный корень: x = " + x); >else < System.out.println("Уравнение не имеет действительных корней"); >> >

Заключение

Мы реализовали программу для решения квадратного уравнения. Вводные данные считываются с помощью Scanner.

Источник