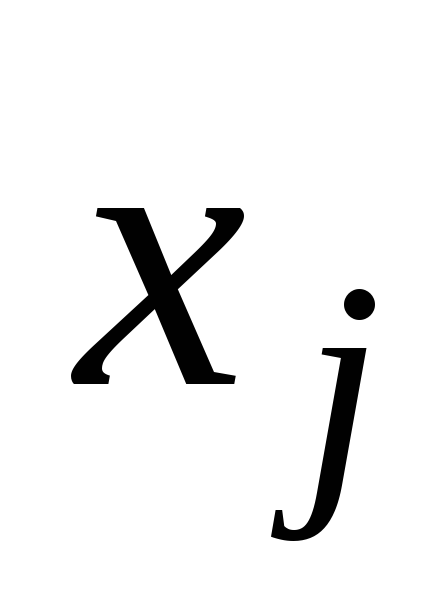Каноническое представление задачи линейного программирования

14. Отыскание исходного опорного базиса.

2) если после приведения системы к единичному базису появились отрицательные свободные элементы, выберем среди них наибольший по абсолютной величине и вычтем почленно выделенное таким образом уравнение из всех остальных уравнений с отрицательными свободными членами. Само же выделенное уравнение перепишем, умножив все коэффициенты на -1;

3) дальнейшие преобразования системы будем проводить согласно правилам однократного замещения, выбирая разрешающий столбец из условия, чтобы он имел в выделенной строке положительный элемент. Для выбора разрешающей строки вычисляем отношения A_io к A_ip и берем в качестве разрешающей строку с минимальным полученным значением;

4) предположим, что после выполнения некоторого количества итераций (3) мы все же не смогли выделить базис полностью и пришли к таблице, в которой выделенная строка не имеет ни одного положительного элемента, кроме свободного члена. Очевидно, что процесс последовательных преобразований на этом обрывается, ибо становится невозможным выбор разрешающего столбца по указанному выше принципу. Нетрудно прийти к выводу, что в этом случае исходная система уравнений не имеет ни одного решения с неотрицательными значениями неизвестных, в том числе и опорного решения, или, как говорят, несовместна в области неотрицательных (допустимых) решений.

В случае, если исходная система имеет хотя бы одно опорное решение, после конечного числа описанных выше итераций будет получено исходное опорное решение.

15. Переход от одного опорного решения к другому.

1) разрешающий столбец (номер p) выбирается так, чтобы в нем оказался хотя бы один положительный элемент A_ip > 0;

2) разрешающая строка (номер q) выбирается из условия, чтобы отношение было наименьшим из значений при A_ip > 0.

Для этого необходимо найти новый базисный столбец, который мы выбираем по следующим правилам:

1)в качестве разрешаюшего столбца выбираем любой свободный столбец, содержащий хотя бы одно положительное число

2)разрешающая строка, в которой б/аi — min

16. Каноническая форма задачи линейного программирования

Канонической формой записи ЗЛП называют задачу

Существуют 5 основных признаков представления задачи линейного программирования в канонической форме:

1)минимизация целевой функции (2.24);

2)запись системы ограничений в виде строгих равенств (2.25);

3)условие неотрицательности на все переменные (2.26);

4)наличие в системе ограничений исходного базиса;

5)неотрицательность всех свободных членов в системе ограничений.

17. Приведение задачи линейного программирования к канонической форме

При необходимости задачу максимизации можно заменить задачей минимизации, и наоборот.

Если в исходной ЗЛП целевая функция максимизируется, т.е.

то выполнив замену Z₁=–Z, получаем новое выражение

Для перехода к канонической форме необходимо заменить все неравенства на строгие равенства.

Пусть исходная ЗЛП имеет вид

Преобразуем ее к каноническому виду. Введем m дополнительных (балансовых) неотрицательных переменных x_n+i  0 ( i = ). Для того чтобы неравенства типа  (2.30) преобразовать в равенства, к их левым частям прибавим дополнительные переменные x_n+i (i = ), после чего система неравенств (2.30) примет вид (2.33)

Для того чтобы неравенства типа  (2.31) преобразовать в равенства, из их левых частей вычтем дополнительные переменные x_n+i ( i = ) . Получим (2.34)

Систему уравнений (2.33), (2.34) с условием неотрицательности дополнительных переменных называют эквивалентной системе неравенств (2.30), (2.31).

Дополнительные переменные x_n+i ( i = ) в целевую функцию вводятся с коэффициентами, равными нулю. Получим задачу:

Задача (2.35)—(2.38) имеет каноническую форму.

В ряде производственно-экономических ситуаций не на все переменные налагаются условия неотрицательности. В подобных ситуациях, даже если ограничения представлены в виде равенств, задача не будет канонической. Для представления такой задачи в каноническом виде каждую из переменных x_k , на которые не наложено условие неотрицательности, заменим разностью двух неотрицательных переменных и , т.е. , где . Очевидно, что при этом мы получим эквивалентную задачу.

Источник

Переход к канонической форме ЗЛП

Каноническая форма ЗЛП — задача линейного программирования вида ax = b , где a — матрица коэффициентов, b — вектор ограничений.

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .

Математическая модель ЗЛП называется основной, если ограничения в ней представлены в виде уравнений при условии неотрицательности переменных.

Математическая модель называется канонической, если ее система ограничений представлена в виде системы m линейно независимых уравнений (ранг системы r=m), в системе выделен единичный базис, определены свободные переменные и целевая функция выражена через свободные переменные. При этом правые части уравнений неотрицательны (b_i ≥ 0).

Переменные, входящие в одно из уравнений системы с коэффициентом один и отсутствующие в других уравнениях называются базисными неизвестными, а все другие – свободными.

Решение системы называется базисным, если в нем свободные переменные равны 0, и оно имеет вид:
X_баз = (0, 0; b₁, …, b_m), f(X_баз) = c₀

Базисное решение является угловой точкой множества решений системы, т.е. определяет вершину многоугольника решений модели. Среди таких решений находится и то, при котором целевая функция принимает оптимальное значение.

Базисное решение называется опорным, если оно допустимо, т.е. все правые части уравнений системы (или неравенств) положительны b_i ≥ 0.

Компактная форма канонической модели имеет вид:
AX = b
X ≥ 0
Z = CX(max)

Понятие допустимого решения, области допустимых решений, оптимального решения задачи линейного программирования.
Определение 1 . Вектор X, удовлетворяющий системе ограничений ЗЛП, в том числе и условиям неотрицательности, если они имеются, называется допустимым решением ЗЛП.
Определение 2 . Совокупность всех допустимых решений образует область допустимых решений (ОДР) ЗЛП.
Определение 3 . Допустимое решение, для которого целевая функция достигает максимума (или минимума), называется оптимальным решением.

• эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
• при этих значениях целевая функция обращалась бы в минимум или максимум.

• неравенства, входящие в систему ограничений задачи, преобразовать в уравнения с помощью введения дополнительных переменных;
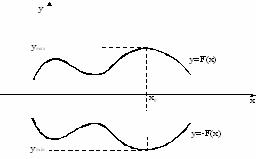
• если целевая функция F→max (максимизируется), она заменяется на функцию –F→ min (которая минимизируется).

Пример №1 . Следующую задачу ЛП привести к каноническому виду: F(X) = 5x₁ + 3x₂ → max при ограничениях:
2x₁ + 3x₂≤20
3x₁ + x₂≤15
4x₁≤16
3x₂≤12
Модель записана в стандартной форме. Введем балансовые неотрицательные переменные x₃, x₄, x₅, x₆, которые прибавим к левым частям ограничений-неравенств. В целевую функцию все дополнительные переменные введем с коэффициентами, равными нулю:
В первом неравенстве смысла (≤) вводим базисную переменную x₃. Во 2-ом неравенстве смысла (≤) вводим базисную переменную x₄. В третьем неравенстве вводим базисную переменную x₅. В 4-м неравенстве — базисную переменную x₆. Получим каноническую форму модели:
2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 20
3x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 15
4x₁ + 0x₂ + 0x₃ + 0x₄ + 1x₅ + 0x₆ = 16
0x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ + 1x₆ = 12
F(X) = 5x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ + 0x₆ → max Пример №2 . Найти два опорных решения системы
x₁ + 2x₄ – 2x₅ = 4
x₃ + 3x₄ + x₅ = 5
x₂ + 3x₅ = 2 Ответ: X = (4;2;5;0;0) Пример №3 . Привести к канонической форме следующую ЗЛП.
F = 2x₁ — x₂ + 4x₃ -2x₄ → min
при ограничениях:
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ ≥ 7
x₁ +x₂ -5x₃ ≤ 11
7x₁ –x₂ -3x₃ — x₄ ≤ 9
x₁ ≥0 , x₂ ≥0 (обратите внимание, что переменные x₃ и x₄ имеют произвольный знак) Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции
— F = -2x₁ + x₂ — 4x₃ +2x₄ → max 2. В левые части трех последних неравенств внести дополнительные переменные x₅, x₆, x₇ со знаком плюс или минус в зависимости от знака неравенства.
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ –x₅ = 7
x₁ +x₂ -5x₃ +x₆ = 11
7x₁ –x₂ -3x₃ — x₄ +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0 3. Так как переменные x₃ и x₄ произвольного знака, то они заменяются разностями неотрицательных переменных.
7x₁ –x₂ +5(x₈ – x₉) + (x₁₀ – x₁₁) = -10
3x₁ +5x₂ -9(x₈ – x₉) + 2(x₁₀ – x₁₁) = 6
x₁ –x₂ -2(x₈ – x₉) + 6(x₁₀ – x₁₁) –x₅ = 7
x₁ +x₂ -5(x₈ – x₉) +x₆ = 11
7x₁ –x₂ -3(x₈ – x₉) — (x₁₀ – x₁₁) +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0 , x₈ ≥0, x₉ ≥0 , x₁₀ ≥0, x₁₁ ≥0 4. Соответствующая целевая функция примет вид:
— F = -2x₁ + x₂ — 4(x₈ – x₉) +2(x₁₀ – x₁₁) → max см. также Как привести каноническую задачу линейного программирования к стандартной форме Пример №2 . Преобразовать следующие задачи ЛП к канонической форме и решить их симплекс-методом.

Источник

4.1. Каноническая форма задачи линейного программирования

Запись целевой функции и системы ограничений в различных задачах линейного программирования неодинаков: в одних задачах требуется найти минимум целевой функции, а в других – максимум; в одних случаях искомые переменные зависят от одного индекса, а в других – от двух; в одних задачах ограничения заданы в виде системы линейных неравенств, а в других – в виде системы линейных уравнений. На практике возможны также задачи, в которых часть ограничений имеет вид линейных неравенств, а часть – линейных уравнений. Также не во всех задачах может требоваться неотрицательность переменных .

Учет такого разнообразия задач линейного программирования требует разработки специальных методов для решения отдельных их классов. Мы же сосредоточим свое внимание на изучении общих свойств и методов линейного программирования, записанных в так называемой канонической форме.

Если в задаче линейного программирования система исходных ограничений приобретает вид уравнений типа

или

и нужно найти максимум линейной целевой функции

,

то считается, что задача линейного программирования записана в канонической форме.

Любую задачу линейного программирования можно легко свести к канонической форме. В общем случае для этого достаточно уметь, во-первых, свести задачу минимизации целевой функции к задаче ее максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам, и в-третьих, менять те переменные, которые не подчинены условию неотрицательности.

В том случае, когда нужно найти минимум функции , можно перейти к нахождению максимума функции , поскольку справедливо утверждение: .

Ограничение-неравенство исходной задачи, которое имеет вид «» , можно превратить в ограничение-уравнение путем добавления к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «»– путем вычитания из его левой части дополнительной неотрицательной переменной.

Заметим, что количество введенных дополнительных неотрицательных переменных всегда равно количеству неравенств в исходной системе ограничений.

Введены дополнительные переменные имеют вполне конкретный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражаются расходы и наличие производственных ресурсов, то числовое значение дополнительной переменной показывает объем соответствующего неиспользованного ресурса.

Отметим также, что если некоторая переменная не подчиняется условию неотрицательности, то ее нужно заменить двумя неотрицавтельными переменными и , приняв .

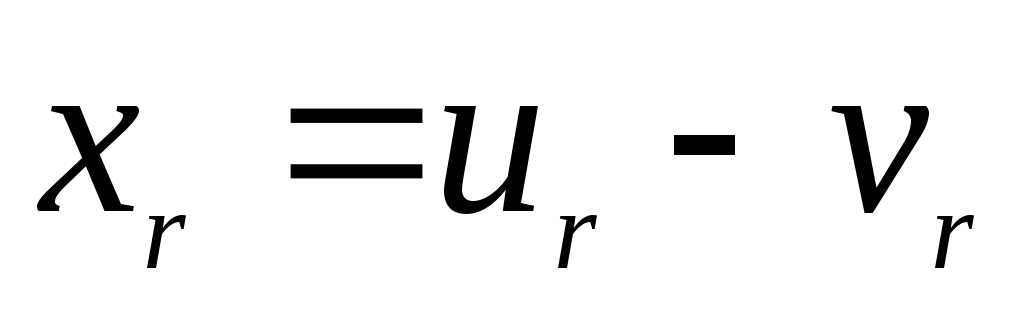
Пример. Записать в канонической форме следующую задачу линейной оптимизации: найти минимум функции при ограничениях

В данной задаче нужно найти минимум целевой функции, а система ограничений включает четыре неравенства. Для того, чтобы записать ее в канонической форме, нужно перейти от ограничений-неравенств к ограничениям-уравнениям, а также превратить целевую функцию.

Так как количество неравенств, входящих в систему ограничений задачи , равно четырем, то этот переход должен быть осуществлен с введением четырех дополнительных неотрицательных переменных. При этом во втором и четвертом неравенствах стоит знак «» , поэтому к их левой части дополнительные переменные добавляем. В первом и третьем неравенствах – знак «», значит от их левой части дополнительные переменные вычитаем.

Также превращаем целевую функцию, поменяв все знаки на противоположные, и находим ее максимум.

Таким образом, данная задача линейного программирования будет записана в следующем каноническом виде:

найти максимум функции

при ограничениях

Источник