Какие деревья бывают программирование

Деревья

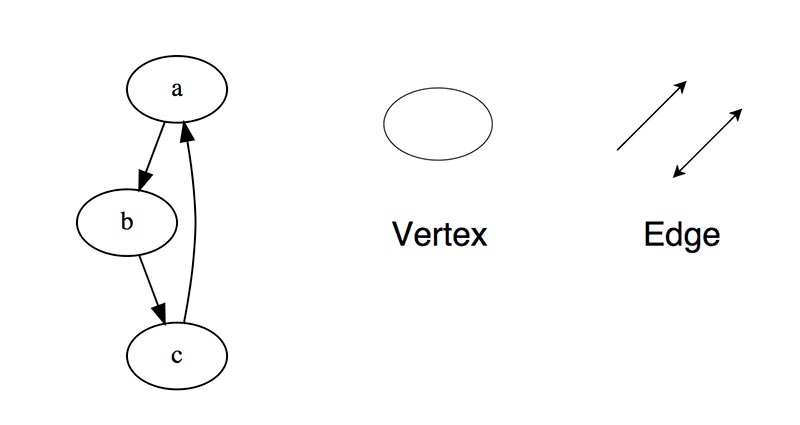
Дерево — это нелинейная иерархическая структура данных. Она состоит из узлов и ребер, которые соединяют узлы.

Зачем нужны деревья

Другие структуры данных, например, массивы, списки, стеки и очереди, линейные. Это значит, что данные в них хранятся последовательно. Когда мы выполняем любую операцию в линейной структуре данных, временная сложность растет с увеличением размера данных. В современном мире это не очень круто.

Разные древовидные структуры позволяют быстрее и легче получать доступ к данным, поскольку дерево — структура нелинейная.

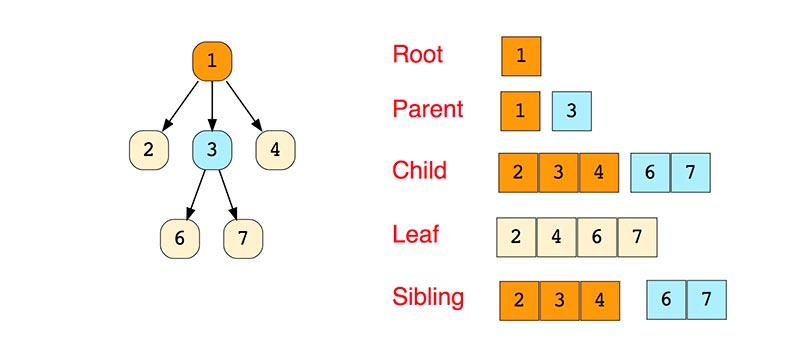
Части дерева

• Узел — это объект, в котором есть ключ или значение и указатели на дочерние узлы.
  Узлы, у которых нет дочерних узлов, называют листами или терминальными узлами.
  Узлы, у которых есть хотя бы один дочерний узел, называются внутренними.
• Ребро связывает два узла.
• Корень — это самый верхний узел дерева. Его ещё иногда называют корневым узлом.

Другие понятия

• Высота узла — это максимальная длина пути от этого узла к самому нижнему узлу (листу).
• Глубина вложенности узла — длина пути от корня до этого узла.
• Высота дерева — это высота корневого узла или глубина самого глубокого узла.
• Степень узла — это общее количество ребер, которые соединены с этим узлом.

• Лес — множество непересекающихся деревьев. Например, если «срезать» корень, получится лес.

Виды деревьев

Обход дерева

Чтобы выполнить какую-либо операцию с деревом, нужно добраться до определенного узла. Для этого и существуют алгоритмы обхода дерева. Они помогают «дойти» до необходимого узла.

Где используются

• Деревья двоичного поиска помогают быстро проверить наличие элемента в наборе.
• Куча — это тоже своеобразное дерево. Кучи используют в алгоритме сортировки кучей.
• Префиксные деревья используются в маршрутизаторах, они хранят информацию о маршруте.
• Большинство популярных баз данных основаны на B-деревья и T-деревья.
• Компиляторы используют абстрактное синтаксическое дерево, чтобы находить синтаксические ошибки в ваших программах.

СodeСhick.io — простой и эффективный способ изучения программирования.

2023 © ООО «Алгоритмы и практика»

Источник

Основные структуры данных. Матчасть. Азы

Все чаще замечаю, что современным самоучкам очень не хватает матчасти. Все знают языки, но мало основы, такие как типы данных или алгоритмы. Немного про типы данных.

Еще в далеком 1976 швейцарский ученый Никлаус Вирт написал книгу Алгоритмы + структуры данных = программы.

40+ лет спустя это уравнение все еще верно. И если вы самоучка и надолго в программировании пробегитесь по статье, можно по диагонали. Можно код кофе.

В статье так же будут вопросы, которое вы можете услышать на интервью.

Что такое структура данных?

Структура данных — это контейнер, который хранит данные в определенном макете. Этот «макет» позволяет структуре данных быть эффективной в некоторых операциях и неэффективной в других.

Какие бывают?

Линейные, элементы образуют последовательность или линейный список, обход узлов линеен. Примеры: Массивы. Связанный список, стеки и очереди.

Нелинейные, если обход узлов нелинейный, а данные не последовательны. Пример: граф и деревья.

Основные структуры данных.

1. Массивы
2. Стеки
3. Очереди
4. Связанные списки
5. Графы
6. Деревья
7. Префиксные деревья
8. Хэш таблицы

Массивы

Массив — это самая простая и широко используемая структура данных. Другие структуры данных, такие как стеки и очереди, являются производными от массивов.

Изображение простого массива размера 4, содержащего элементы (1, 2, 3 и 4).

Каждому элементу данных присваивается положительное числовое значение (индекс), который соответствует позиции элемента в массиве. Большинство языков определяют начальный индекс массива как 0.

Бывают

Одномерные, как показано выше.
Многомерные, массивы внутри массивов.

Основные операции

• Insert-вставляет элемент по заданному индексу
• Get-возвращает элемент по заданному индексу
• Delete-удаление элемента по заданному индексу
• Size-получить общее количество элементов в массиве

Вопросы

• Найти второй минимальный элемент массива
• Первые неповторяющиеся целые числа в массиве
• Объединить два отсортированных массива
• Изменение порядка положительных и отрицательных значений в массиве

Стеки

Стек — абстрактный тип данных, представляющий собой список элементов, организованных по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).

Это не массивы. Это очередь. Придумал Алан Тюринг.

Примером стека может быть куча книг, расположенных в вертикальном порядке. Для того, чтобы получить книгу, которая где-то посередине, вам нужно будет удалить все книги, размещенные на ней. Так работает метод LIFO (Last In First Out). Функция «Отменить» в приложениях работает по LIFO.

Изображение стека, в три элемента (1, 2 и 3), где 3 находится наверху и будет удален первым.

Основные операции

• Push-вставляет элемент сверху
• Pop-возвращает верхний элемент после удаления из стека
• isEmpty-возвращает true, если стек пуст
• Top-возвращает верхний элемент без удаления из стека

Вопросы

• Реализовать очередь с помощью стека
• Сортировка значений в стеке
• Реализация двух стеков в массиве
• Реверс строки с помощью стека

Очереди

Подобно стекам, очередь — хранит элемент последовательным образом. Существенное отличие от стека – использование FIFO (First in First Out) вместо LIFO.

Пример очереди – очередь людей. Последний занял последним и будешь, а первый первым ее и покинет.

Изображение очереди, в четыре элемента (1, 2, 3 и 4), где 1 находится наверху и будет удален первым

Основные операции

• Enqueue—) — вставляет элемент в конец очереди
• Dequeue () — удаляет элемент из начала очереди
• isEmpty () — возвращает значение true, если очередь пуста
• Top () — возвращает первый элемент очереди

Вопросы

• Реализовать cтек с помощью очереди
• Реверс первых N элементов очереди
• Генерация двоичных чисел от 1 до N с помощью очереди

Связанный список

Связанный список – массив где каждый элемент является отдельным объектом и состоит из двух элементов – данных и ссылки на следующий узел.

Принципиальным преимуществом перед массивом является структурная гибкость: порядок элементов связного списка может не совпадать с порядком расположения элементов данных в памяти компьютера, а порядок обхода списка всегда явно задаётся его внутренними связями.

Бывают

Однонаправленный, каждый узел хранит адрес или ссылку на следующий узел в списке и последний узел имеет следующий адрес или ссылку как NULL.

Двунаправленный, две ссылки, связанные с каждым узлом, одним из опорных пунктов на следующий узел и один к предыдущему узлу.

Круговой, все узлы соединяются, образуя круг. В конце нет NULL. Циклический связанный список может быть одно-или двукратным циклическим связанным списком.

Самое частое, линейный однонаправленный список. Пример – файловая система.

Основные операции

• InsertAtEnd — Вставка заданного элемента в конец списка
• InsertAtHead — Вставка элемента в начало списка
• Delete — удаляет заданный элемент из списка
• DeleteAtHead — удаляет первый элемент списка
• Search — возвращает заданный элемент из списка
• isEmpty — возвращает True, если связанный список пуст

Вопросы

• Реверс связанного списка
• Определение цикла в связанном списке
• Возврат N элемента из конца в связанном списке
• Удаление дубликатов из связанного списка

Графы

Граф-это набор узлов (вершин), которые соединены друг с другом в виде сети ребрами (дугами).

Бывают

Ориентированный, ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
Неориентированные, к каждому из ребер можно осуществлять переход в обоих направлениях.
Смешанные

Встречаются в таких формах как

Общие алгоритмы обхода графа

Вопросы

• Реализовать поиск по ширине и глубине
• Проверить является ли граф деревом или нет
• Посчитать количество ребер в графе
• Найти кратчайший путь между двумя вершинами

Деревья

Дерево-это иерархическая структура данных, состоящая из узлов (вершин) и ребер (дуг). Деревья по сути связанные графы без циклов.

Древовидные структуры везде и всюду. Дерево скилов в играх знают все.

• N дерево
• Сбалансированное дерево
• Бинарное дерево
• Дерево Бинарного Поиска
• AVL дерево
• 2-3-4 деревья

«Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. » — Procs

Три способа обхода дерева

• В прямом порядке (сверху вниз) — префиксная форма.
• В симметричном порядке (слева направо) — инфиксная форма.
• В обратном порядке (снизу вверх) — постфиксная форма.

Вопросы

• Найти высоту бинарного дерева
• Найти N наименьший элемент в двоичном дереве поиска
• Найти узлы на расстоянии N от корня
• Найти предков N узла в двоичном дереве

Trie ( префиксное деревое )

Разновидность дерева для строк, быстрый поиск. Словари. Т9.

Вот как такое дерево хранит слова «top», «thus» и «their».

Слова хранятся сверху вниз, зеленые цветные узлы «p», «s» и «r» указывают на конец «top», «thus « и «their» соответственно.

Вопросы

• Подсчитать общее количество слов
• Вывести все слова
• Сортировка элементов массива с префиксного дерева
• Создание словаря T9

Хэш таблицы

Хэширование — это процесс, используемый для уникальной идентификации объектов и хранения каждого объекта в заранее рассчитанном уникальном индексе (ключе).

Объект хранится в виде пары «ключ-значение», а коллекция таких элементов называется «словарем». Каждый объект можно найти с помощью этого ключа.

По сути это массив, в котором ключ представлен в виде хеш-функции.

Эффективность хеширования зависит от

• Функции хеширования
• Размера хэш-таблицы
• Метода борьбы с коллизиями

Пример сопоставления хеша в массиве. Индекс этого массива вычисляется через хэш-функцию.

Вопросы

• Найти симметричные пары в массиве
• Найти, если массив является подмножеством другого массива
• Описать открытое хеширование

Список ресурсов

Вместо заключения

Матчасть так же интересна, как и сами языки. Возможно, кто-то увидит знакомые ему базовые структуры и заинтересуется.

Спасибо, что прочли. Надеюсь не зря потратили время =)

PS: Прошу извинить, как оказалось, перевод статьи уже был тут и очень недавно, я проглядел.
Если интересно, вот она, спасибо Hokum, буду внимательнее.

Источник