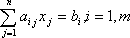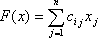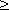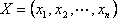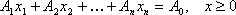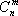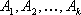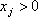Какая задача является задачей линейного программирования ответ

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

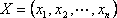
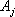
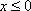
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

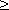
Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

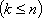
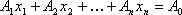
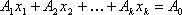
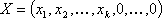
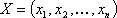
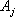
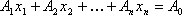
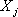
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 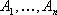имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

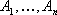
Симплексный метод решения задачи линейного программирования.

Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов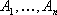. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник

Задачи линейного программирования

Линейное программирование — это раздел математики, занимающийся решением таких задач на отыскание наибольших и наименьших значений, для которых методы математического анализа оказываются непригодными. Другими словами термин «линейное программирование» характеризует определение программы (плана) работы конкретного экономического объекта на основе выявления линейных связей между его элементами. Задачей линейного программирования является нахождение оптимального, т. е. наилучшего, плана при заданной системе налагаемых на решение ограничений.

К классу задач линейного программирования относится большое количество разнообразных задач планирования и управления, как, например:

1. нахождение оптимального плана выпуска продукции (оптимальное распределение ресурсов);
2. оптимизация межотраслевых потоков (планирование производства различных видов продукции по отраслям);
3. определение оптимального рациона (оптимизация состава химической смеси);
4. транспортная задача (оптимальное распределение потоков товарных поставок по транспортной сети);
5. задача о размещении производства (планирование с учётом затрат на производство и транспортировку продукции);
6. задача о назначениях (оптимальное распределение различных видов транспортных средств) и др.

Пример построения математической модели задачи

Предприятие изготавливает и продает краску двух видов: для внутренних и внешних работ. Для производства краски используется три исходных продуктаS1,S2 иS3. Расходы продуктов и запасы этих продуктов на складе приведены в таблице:

Исходный продукт	Расход продуктов (в тоннах на 1 т. краски)		Запас продукта на складе (тонн)
	краска для внутренних работ	краска для внешних работ
S1	10	5	250
S2	20	20	500
S3	5	5	200

Выпуск 1 тонны краски для внутренних работ приносит предприятию прибыль в размере 200 денежных единиц (ден. ед.), для внешних работ — 200 ден. ед. Требуется определить, сколько краски каждого вида следует производить предприятию, чтобы получить максимальный доход (при соблюдении ограничений на ресурсы). 1) Введем переменные задачи: Обозначим x₁— количество производимой краски для внутренних работ;x₂— соответствующее количество краски для наружных работ. 2) Ограничения, которым должны удовлетворять переменные задачи: Учитывая количество каждого вида сырья для производства краски, а также запасы сырья и прибыль, получаемую от выпуска изделий, составим соответствующие ограничения. 3) Целевая функция задачи: Обозначим Zдоход от продажи краски, тогда целевая функция задачи записывается так: Z= 200х₁ + 200х₂ Таким образом, задача состоит в том, чтобы найти максимум целевой функции Z= 200х₁ + 200х₂при ограничениях Это и есть математическая модель задачи.

Практическое занятие №2

Наименование занятия:Решение задач линейного программирования графическим методомЦель занятия: Научиться составлять математическую модель задачи линейного программирования, решать ее графическим методом. Подготовка к занятию: Повторить теоретический материал по теме «Линейное программирование» Литература:

1. Лобачева М.Е. Конспект лекций «Математические методы», 2013г.
2. Агальцов В.П. Математические методы в программировании, 2010г.

Перечень необходимых приборов, инструментов, материалов:ПЭВМ Задание на занятие:Задание 1.Решить задачу линейного программирования графическим методом

Вариант	Вариант
1		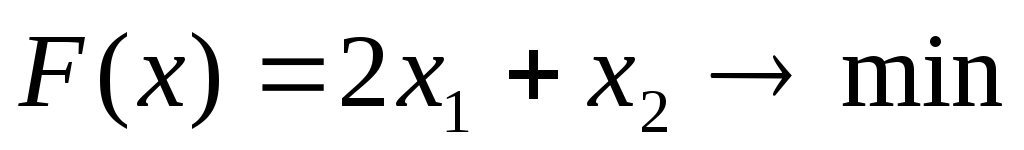6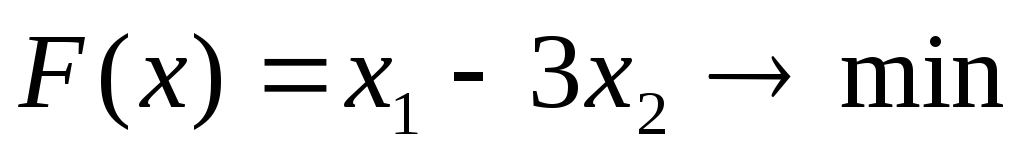
2		7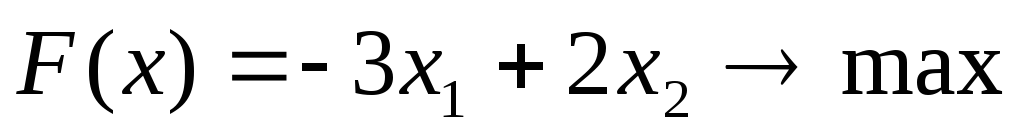
3		8
4		9
5		10

Задание 2. Составить математическую модель задачи и решить ее графическим методом Один из цехов предприятия выпускает изделия двух видов: А и В. Для производства этих изделий требуются три вида сырья: S1,S2 иS3. На выпуск изделия А расходуется D1 кгS1, D2 кгS2 и D3 кгS3. На выпуск изделия В расходуется F1 кгS1, F2 кгS2 и F3 кгS3. Запасы ресурсов ограничены: за рабочую смену цех может израсходовать не более G1 кгS1, G2 кгS2 и G3 кгS3. Выпуск изделия А приносит предприятию прибыль в размере Р1 денежных единиц (ден. ед.), изделия В — Р2 ден. ед. Требуется составить оптимальный план работы цеха, т.е. найти, сколько изделий А и изделий В требуется выпускать, чтобы получить максимальную прибыль (при соблюдении ограничений на ресурсы).

Вариант	D1	D2	D3	F1	F2	F3	G1	G2	G3	P1	P2
1	5	10	20	20	5	5	500	250	200	300	100
2	15	10	10	10	10	10	400	200	350	150	250
3	10	15	10	10	15	5	200	400	350	250	150
4	15	15	5	15	5	15	450	250	250	200	200
5	10	20	5	5	20	5	250	500	200	200	200
6	5	15	15	15	5	15	250	250	450	200	200
7	5	15	15	15	15	5	250	400	250	200	200
8	10	15	10	15	10	10	300	300	250	250	150
9	15	10	10	10	10	15	300	250	300	250	150
10	10	10	15	10	15	10	250	300	300	150	250

Порядок проведения занятия:

1. Получить допуск к работе;
2. Выполнить задания в соответствии со своим вариантом;
3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель работы, задание;
2. Выполненное задание;
3. Выводы по результатам выполненного задания;
4. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Какие задачи относятся к задачам линейного программирования?
2. Запишите общий вид задачи линейного программирования.
3. Геометрический метод решения задач линейного программирования, его достоинства и недостатки
4. Как определяется область допустимых решений?
5. Перечислите основные этапы решения задачи ЛПР графическим способом.

ПРИЛОЖЕНИЕ

Источник