Arrays, Collections: Алгоритмический минимум
Недавно на собеседовании в крупную компанию на должность Java разработчика меня попросили реализовать стандартный алгоритм сортировки. Поскольку я никогда не реализовывал самописные алгоритмы сортировки, а пользовался всегда готовыми решениями, у меня возникли затруднения с реализацией. После собеседования я решил разобраться в вопросе и подготовить список основных алгоритмов сортировки и поиска, которые используются в стандартном пакете java — Java Collections Framework (JCF). Для этого я изучил исходники Oracle JDK 7.80 (UPD: добавлена ссылка).
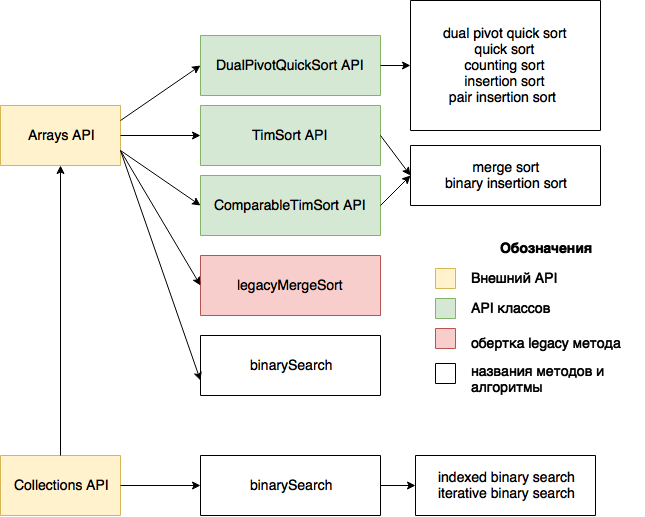
В самом обобщенном виде результат изучения представлен на рисунке. Подробности — в основном тексте.
Рисунок 1. Методы Arrays, Collections и реализуемые ими алгоритмы
Первое, что поразило меня в алгоритмах, реализованных в Arrays и Collections — то, что их можно буквально по пальцам пересчитать — по большому счету, это два алгоритма сортировки и один алгоритм поиска.
Второе — то, что сортировка списков «под капотом» использует сортировку массивов.
Третье — то, что один из алгоритмов сортировки портирован с python.
Алгоритм быстрой сортировки с двумя опорными элементами разработан нашим соотечественником Владимиром Ярославским и реализован при содействии Джона Бентли и Джошуа Блоха.
Алгоритм сортировки слиянием, который является основным для сортировки массивов ссылочных типов, буквально назван по имени своего создателя Tim Peters — TimSort. Этот алгоритм был адаптирован Джошуа Блохом с алгоритма сортировки списков, реализованном на python Тимом Петерсом.
Кратко излагая результаты, стоит отметить, что:
- Можно условно выделить три слоя методов:
- Методы API
- Методы базовых (основных) алгоритмов
- Методы (блоки) дополнительных алгоритмов
- Основных алгоритмов используется три. Два алгоритма сортировки: быстрая сортировка, сортировка слиянием. Один алгоритм поиска: бинарный поиск.
- Для оптимизации «основные» алгоритмы заменяются на более подходящие в данный момент “дополнительные” алгоритмы (полный список алгоритмов и условий переключения приведен в конце)
- Для определения того, какой из «дополнительных» алгоритмов будет задействован, могут использоваться:
- сигнатуры методов (типы аргументов, булевы переменные)
- флаги VM
- пороговые значения длины массива/списка, хранящиеся в приватных переменных классов
Итак, для того, чтобы выяснить, какие основные и дополнительные алгоритмы используются в пакете util, нужно разобрать реализацию 4-х методов из API Collections и API Arrays.
Таблица 1. API Arrays vs API Collections
| Метод | Arrays API | Collections API |
|---|---|---|
| Sort method | Arrays.sort | Collections.sort |
| Search method | Arrays.binarySearch | Collections.binarySearch |
Arrays.sort
Массивы примитивных типов
Основной алгоритм сортировки для массивов примитивных типов в Arrays — быстрая сортировка. Для реализации этой сортировки выделен финальный класс DualPivotQuickSort, который предоставляет публичные методы sort для сортировки массивов всех примитивных типов данных. Методы Arrays API вызывают эти методы и пробрасывают в них ссылку на массив. Если требуется отсортировать определенный диапазон массива, то передаются еще и индексы начала и конца диапазона.
Временная сложность алгоритма быстрой сортировки в лучшем случае и в среднем случае составляет O(n log n). В некоторых случаях (например, на малых массивах) алгоритм быстрой сортировки обладает не лучшей производительностью, деградирует до квадратичной сложности. Поэтому имеет смысл вместо него применять другие алгоритмы, которые в общем случае проигрывают, но в конкретных случаях могут дать выигрыш. В качестве дополнительных алгоритмов были выбраны сортировка вставками, “обычная” быстрая сортировка (с одной опорной точкой), сортировка подсчетом.
Инженеры Oracle эмпирическим путем вычислили оптимальные размерности массивов для задействования каждого дополнительного алгоритма сортировки. Эти значения записаны в приватных полях класса DualPivotQuickSort. Для наглядности я свел их в таблицу 2.
Таблица 2. Дополнительные алгоритмы в DualPivotQuickSort.sort
| Типы данных | Размер массива, n | Предпочитаемый алгоритм | Временная сложность в лучшем случае |
|---|---|---|---|
| int, long, short, char, float, double | n < 47 | insertion sort, pair insertion sort | O(n) |
| int, long, short, char, float, double | n < 286 | quick sort | O(n log n) |
| byte | 29 < n | counting sort | O(n+k) |
| short, char | 3200 < n | counting sort | O(n+k) |
В теле методов DualPivotQuickSort.sort производятся проверки на длину массива, и в зависимости от результата применяется либо основной, либо дополнительный алгоритм.
Массивы примитивных типов. Выбор алгоритма и булев параметр leftmost
Параметр leftmost при необходимости передается в метод sort и показывает, является ли указанная часть самой левой в диапазоне. Если да, то применяется алгоритм “обычной” сортировки вставками. Если нет, то применяется парная сортировка вставками.
Еще одно объяснение о выборе дополнительных алгоритмов можно почитать
здесь.
Массивы ссылочных типов
Для массивов ссылочных типов в качестве основного предусмотрен алгоритм сортировки слиянием, он реализован в трех вариациях. Две актуальные реализации вынесены в специальные классы: TimSort, ComparableTimSort. TimSort предназначена для сортировки объектов с использованием компараторов. ComparableTimSort — это версия TimSort, предназначенная для сортировки объектов, поддерживающих Comparable. Подробности реализации сортировки TimSort смотрите в посте на хабре.
Класс TimSort содержит единственную пороговую величину, при сравнении с которой принимается решение о переключении на дополнительный алгоритм. Это величина называется MIN_MERGE и хранит минимальную длину массива, при которой будет производиться сортировка слиянием. Если же длина массива будет меньше MIN_MERGE, т.е. 32, то будет задействована бинарная сортировка вставками. Как сказано в документации, это мини-TimSort, т.е. без использования слияний.
Таблица 3. Дополнительные алгоритмы в TimSort.sort и ComparableTimSort.sort
| Тип данных | Размер массива, n | Предпочитаемый алгоритм | Временная сложность в лучшем случае |
|---|---|---|---|
| T[] | n < 32 | binary insertion sort | O(n) |
Третья реализация сортировки слиянием является legacy и оставлена для сохранения обратной совместимости с версией JDK 1.6 и более ранними. Legacy сортировка обернута в метод legacyMergeSort и непосредственно реализована в методе Arrays.mergeSort. Для того, чтобы ее использовать, необходимо выставить флаг -Djava.util.Arrays.useLegacyMergeSort=true перед запуском виртуальной машины. Для хранения значения этой переменной в Arrays имеется внутренний статический класс LegacyMergeSort (см. Листинг. 1).
Листинг 1. Статический внутренний класс LegacyMergeSort в Arrays
static final class LegacyMergeSort
При вызове Arrays.sort с массивом ссылочного типа происходит проверка, выставлен ли флаг на применение legacy сортировки. Тогда происходит вызов либо legacy сортировки, либо одной из базовых (см. Листинг 2).
Листинг 2. Реализация метода Arrays.sort для массива ссылочного типа с компаратором
public static void sort(T[] a, Comparator c)
Arrays.binarySearch
Для массивов как примитивных, так и ссылочных типов предусмотрен бинарный поиск. Перед поиском массив должен быть отсортирован. Сложность алгоритма бинарного поиска в среднем и в худшем случае составляет O(log n). Дополнительных алгоритмов не предусмотрено.
Collections.sort
В Collections сортировка предусмотрена только для списков. Интересно, что сначала производится преобразование списка в массив с последующим применением сортировки слиянием для массивов ссылочных типов. Сортировка осуществляется вызовом метода Arrays.sort.
Collections.binarySearch
Как и в случае с сортировкой, в Collections бинарный поиск реализован только для списков. Переменная BINARYSEARCH_THRESHOLD устанавливает ограничение на размер списка в 5000 элементов. Так что если вам необходимо провести поиск на более внушительной выборке, придется подумать, как это лучше сделать.
Списки поддерживают либо произвольный доступ, либо последовательный. Если список поддерживает произвольный доступ, то он будет обрабатываться алгоритмом индексированного бинарного поиска. Если список поддерживает последовательный доступ, то он будет обрабатываться алгоритмом итеративного бинарного поиска. Как видно, и в том, и в другом случае будет применяться бинарный поиск.
Всего интерфейс List в JDK 7.8 реализуют 10 классов, 2 из которых — абстрактные AbstractList и AbstractSequentialList. Последовательный доступ реализует только LinkedList и все потомки AbstractSequentialList. Поэтому они будут обрабатываться алгоритмом iteratorBinarySearch. Остальные списки, такие как ArrayList, CopyOnWriteArrayList, будут обрабатываться алгоритмом indexedBinarySearch.
UPD. Как стало понятно из личной дискуссии с Zamyslov, необходимо уточнить, каким образом BINARYSEARCH_THRESHOLD участвует в определении типа алгоритма сортировки. Это пороговое значение имеет влияние только на списки с последовательным доступом.
Cписок, поддерживающий произвольный доступ, будет всегда обрабатываться Collections.indexedBinarySearch. А список, поддерживающий последовательный доступ, будет обрабатываться Collections.iteratorBinarySearch только если он будет превышать значение BINARYSEARCH_THRESHOLD (см. листинг 3), в противном случае он также будет обрабатываться Collections.indexedBinarySearch.
Листинг 3. Влияние типов списков и константы BINARYSEARCH_THRESHOLD на определение алгоритмов обработки списка
int binarySearch(List> list, T key)
Обобщаем изученное
Теперь, когда рассмотрены основные методы и условия перехода к дополнительным методам, можно обобщить полученные данные. Для максимальной наглядности детализируем рисунок 1, выделив на нем основные методы и добавим условия перехода к дополнительным методам.
Рисунок 2. Основные и дополнительные алгоритмы Arrays, Collections
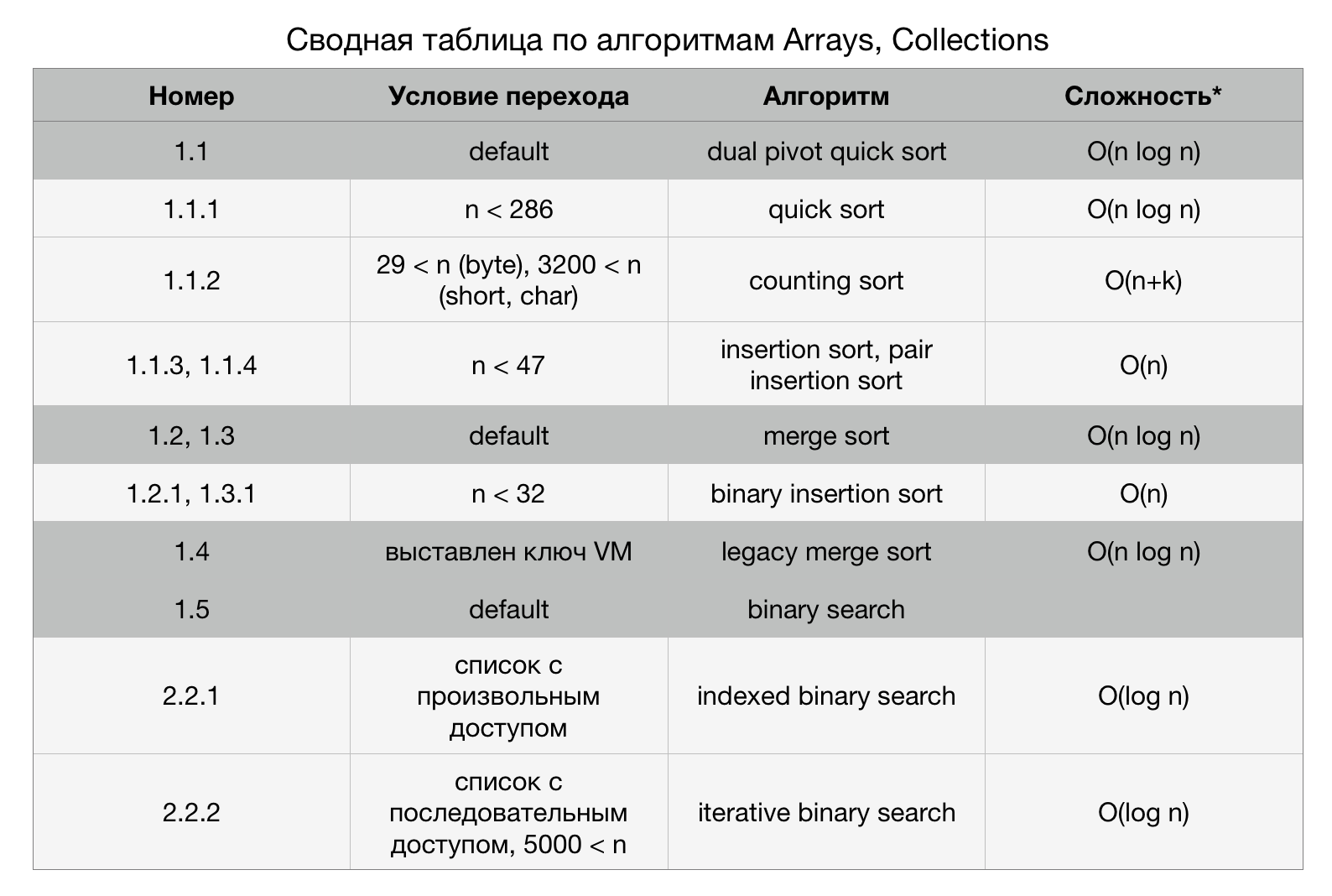
Пояснения к цифрам на стрелках рисунка 2 содержатся в Сводной таблице. Цифры обозначают условия перехода. Серым выделены основные алгоритмы. Они применяются по умолчанию. В Сводной таблице строки, описывающие основные алгоритмы, выделены темно-серым.
*Сложности для основных алгоритмов приведены «в среднем случае», а сложности дополнительных алгоритмов приведены «в лучшем случае».
Заключение
Целью заметки было составить полный список алгоритмов, применяющихся для поиска и сортировки массивов и списков в пакете java.util. Итак, для того, чтобы в полной мере понимать, что происходит “под капотом” при использовании API Arrays и API Collections достаточно владеть следующими алгоритмами:
- быстрая сортировка с двумя опорными точками
- быстрая сортировка с одной опорной точкой
- сортировка подсчетом
- «простая» сортировка вставками
- бинарная сортировка вставками
- парная сортировка вставками
- сортировка слиянием (версия Тима Петерса)
- бинарный поиск
- индексированный бинарный поиск
- итеративный бинарный поиск
Как правильно делать сортировку в Java
Анализируя исходные коды многих opensource Java-проектов, я обнаружил, что большинство разработчиков осуществляют сортировку всего двумя разными способами. Один из них основан на применении метода sort() классов Collections или Arrays , а другой на использовании самосортирующихся структур данных, таких как TreeMap и TreeSet .
Использование метода sort()
// Collections.sort(…) List list = new ArrayList(); Collections.sort(list, new Comparator() < public int compare(ObjectName o1, ObjectName o2) < return o1.toString().compareTo(o2.toString()); >>); // Arrays.sort(…) ObjectName[] arr = new ObjectName[10]; Arrays.sort(arr, new Comparator() < public int compare(ObjectName o1, ObjectName o2) < return o1.toString().compareTo(o2.toString()); >>); Применение самосортирующихся структур данных
Если нужно отсортировать список ( List ) или множество ( Set ), используйте структуру TreeSet для сортировки.
// TreeSet Set sortedSet = new TreeSet(new Comparator() < public int compare(ObjectName o1, ObjectName o2) < return o1.toString().compareTo(o2.toString()); >>); sortedSet.addAll(unsortedSet); Если вам требуется отсортировать словарь ( Map ), используйте структуру TreeMap для сортировки. TreeMap сортируется по ключу ( key ).
// TreeMap – использующий String ключи и компаратор (Comparator) CASE_INSENSITIVE_ORDER, // упорядочивающий строки (String) методом compareToIgnoreCase Map sortedMap = new TreeMap(String.CASE_INSENSITIVE_ORDER); sortedMap.putAll(unsortedMap); //TreeMap – общий случай, компаратор указывается вручную Map sortedMap = new TreeMap(new Comparator() < public int compare(ObjectName o1, ObjectName o2) < return o1.toString().compareTo(o2.toString()); >>); sortedMap.putAll(unsortedMap); Вышеописанный подход очень полезен в тех случаях, если вам нужно проводить большое количество операций поиска элементов в коллекции. Самосортирующиеся структуры данных имеют эффективность O(log(n)) , что лучше, чем O(n) . Это означает, что при удвоении количества данных в коллекции время поиска не удваивается, а увеличивается на постоянную величину (прим. перев.)
Плохой подход к задаче сортировки
До сих пор можно встретить примеры, когда программисты самостоятельно описывают алгоритмы сортировки. Рассмотрим код сортировки, представленный ниже (сортировка double-массива по возрастанию (прим. перев.)). Этот код не только не эффективен, но и не читабелен. И таких примеров много.