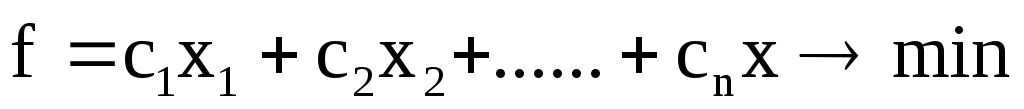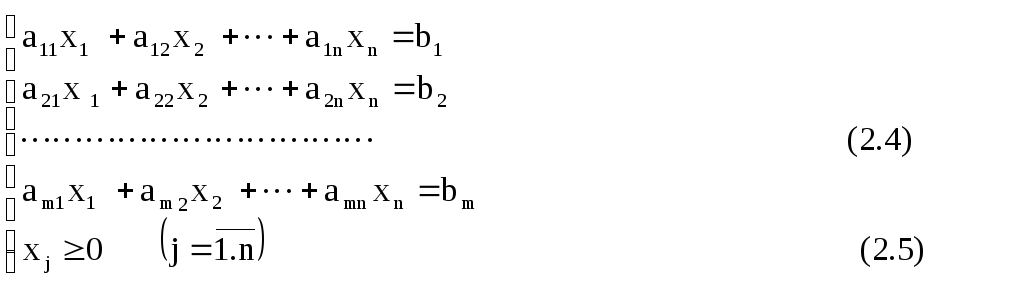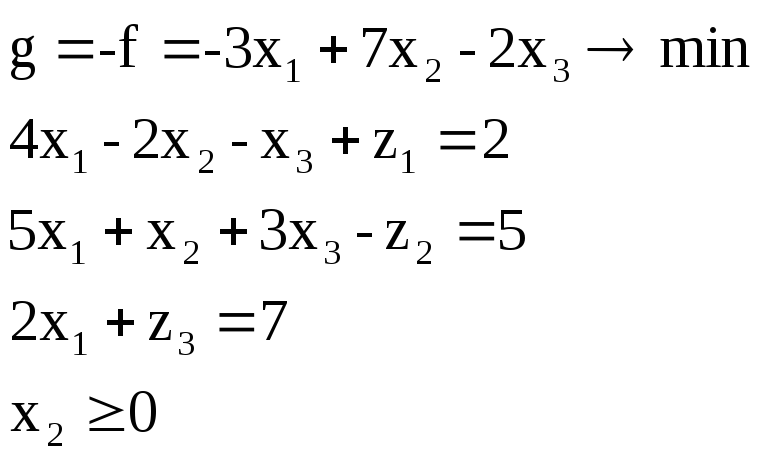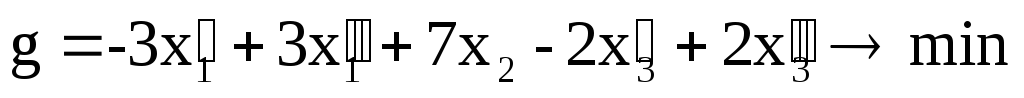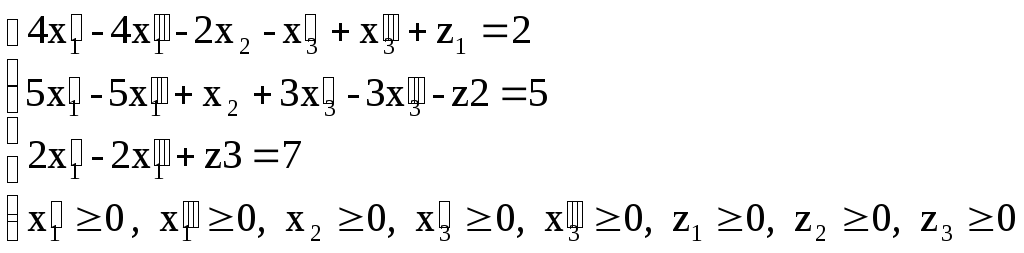Решение задач линейного программирования
Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.
- Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
- Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
- Решение симплексным методом;
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .
Переход от задачи минимизации целевой функции к задаче максимизации
Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:
| F(x) → min | F(x) → max |
Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).
Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).
Переменные x1, …, xm, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (xm+1,…, xn) называются небазисными или независимыми переменными.
Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных xj≥0, что эквивалентно условию неотрицательности bj≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел bj есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.
Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x1 + 2x2 — 2x3 → min при ограничениях:
4x1 + 3x2 — x3≤10
— 2x2 + 5x3≥3
x1 + 2x3=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x4; во втором неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус.
4x1 + 3x2-1x3 + 1x4 + 0x5 = 10
0x1-2x2 + 5x3 + 0x4-1x5 = 3
1x1 + 0x2 + 2x3 + 0x4 + 0x5 = 9
F(X) = — x1 — 2x2 + 2x3
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 4 | 3 | -1 | 1 | 0 | 10 |
| 0 | -2 | 5 | 0 | -1 | 3 |
| 1 | 0 | 2 | 0 | 0 | 9 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x4.
2. В качестве базовой переменной выбираем x2.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(0 • 3):-2 | 3-(-2 • 3):-2 | -1-(5 • 3):-2 | 1-(0 • 3):-2 | 0-(-1 • 3):-2 | 10-(3 • 3):-2 |
| 0 : -2 | -2 : -2 | 5 : -2 | 0 : -2 | -1 : -2 | 3 : -2 |
| 1-(0 • 0):-2 | 0-(-2 • 0):-2 | 2-(5 • 0):-2 | 0-(0 • 0):-2 | 0-(-1 • 0):-2 | 9-(3 • 0):-2 |
Получаем новую матрицу:
| 4 | 0 | 6 1 /2 | 1 | -1 1 /2 | 14 1 /2 |
| 0 | 1 | -2 1 /2 | 0 | 1 /2 | -1 1 /2 |
| 1 | 0 | 2 | 0 | 0 | 9 |
3. В качестве базовой переменной выбираем x3.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x3, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x3 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
| 4-(1 • 6 1 /2):2 | 0-(0 • 6 1 /2):2 | 6 1 /2-(2 • 6 1 /2):2 | 1-(0 • 6 1 /2):2 | -1 1 /2-(0 • 6 1 /2):2 | 14 1 /2-(9 • 6 1 /2):2 |
| 0-(1 • -2 1 /2):2 | 1-(0 • -2 1 /2):2 | -2 1 /2-(2 • -2 1 /2):2 | 0-(0 • -2 1 /2):2 | 1 /2-(0 • -2 1 /2):2 | -1 1 /2-(9 • -2 1 /2):2 |
| 1 : 2 | 0 : 2 | 2 : 2 | 0 : 2 | 0 : 2 | 9 : 2 |
Получаем новую матрицу:
| 3 /4 | 0 | 0 | 1 | -1 1 /2 | -14 3 /4 |
| 1 1 /4 | 1 | 0 | 0 | 1 /2 | 9 3 /4 |
| 1 /2 | 0 | 1 | 0 | 0 | 4 1 /2 |
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /4x1 + x4 — 1 1 /2x5 = -14 3 /4
1 1 /4x1 + x2 + 1 /2x5 = 9 3 /4
1 /2x1 + x3 = 4 1 /2
Выразим базисные переменные через остальные:
x4 = — 3 /4x1 + 1 1 /2x5-14 3 /4
x2 = — 1 1 /4x1 — 1 /2x5+9 3 /4
x3 = — 1 /2x1+4 1 /2
Подставим их в целевую функцию:
F(X) = — x1 — 2(- 1 1 /4x1 — 1 /2x5+9 3 /4) + 2(- 1 /2x1+4 1 /2)
или
F(X) = 1 /2x1 + x5-10 1 /2 → max
Система неравенств:
— 3 /4x1 + 1 1 /2x5-14 3 /4 ≥ 0
— 1 1 /4x1 — 1 /2x5+9 3 /4 ≥ 0
— 1 /2x1+4 1 /2 ≥ 0
Приводим систему неравенств к следующему виду:
3 /4x1 — 1 1 /2x5 ≤ -14 3 /4
1 1 /4x1 + 1 /2x5 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x5-10 1 /2 → max
Упростим систему.
3 /4x1 — 1 1 /2x2 ≤ -14 3 /4
1 1 /4x1 + 1 /2x2 ≤ 9 3 /4
1 /2x1 ≤ 4 1 /2
F(X) = 1 /2x1 + x2-10 1 /2 → max
2.6. Канонический вид злп.
В исходной постановке ЗЛП могут допускать различные формы записи. Так, в одних задачах требуется максимизировать целевую функцию, в других — минимизировать; некоторые линейные ограничения могут иметь вид равенств, другие — неравенств и т.д.
Для единообразия записи ЗЛП вводится так называемая каноническая форма записи.
Говорят, что ЗЛП записана в канонической форме, если она имеет следующий вид:
(2.3)
Отметим следующие особенности канонического вида:
1) требуется минимизировать целевую функцию;
2) все линейные ограничения, кроме требований неотрицательности переменных, имеют вид равенств;
- на все переменные наложены требования неотрицательности.
Покажем, что любую ЗЛП можно привести к каноническому виду. 1) Если в ЗЛП требуется максимизировать целевую функцию f, то положим g = — f и потребуем минимизировать функцию g. Получится новая ЗЛП, которая эквивалентна исходной в том смысле, что каждое оптимальное решение исходной задачи будет оптимальным решением новой задачи и наоборот. 2) Предположим, что в ЗЛП есть линейное ограничение вида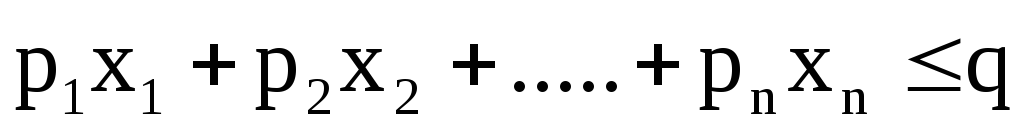 
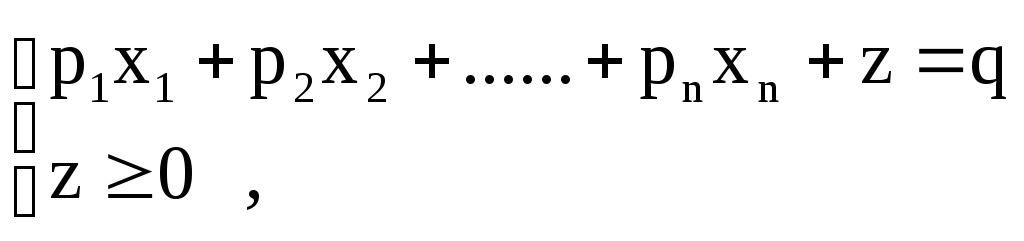
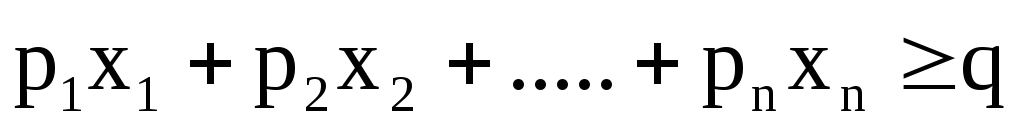
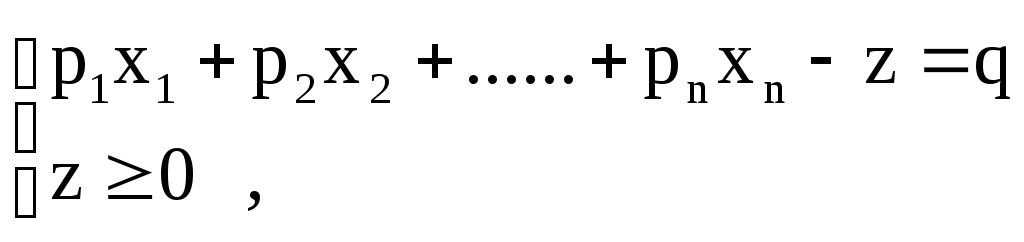
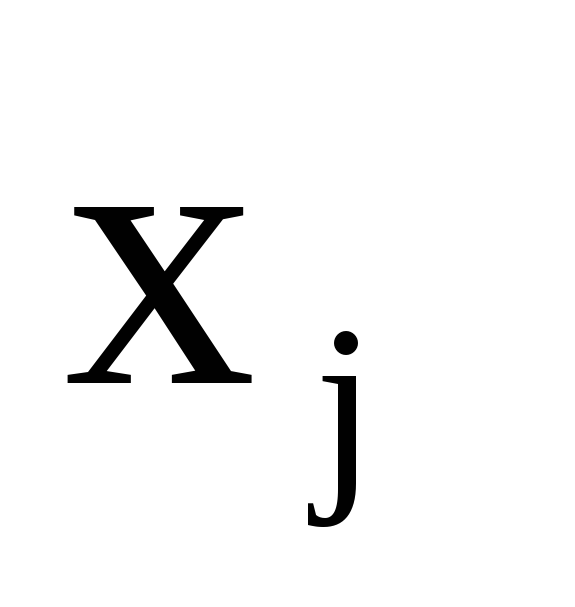
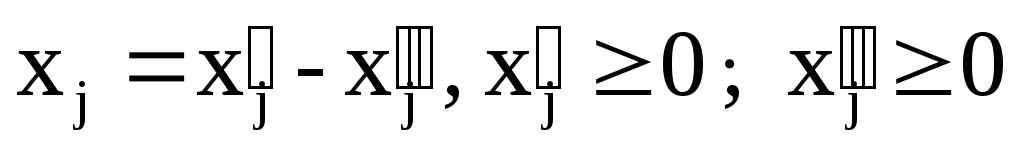
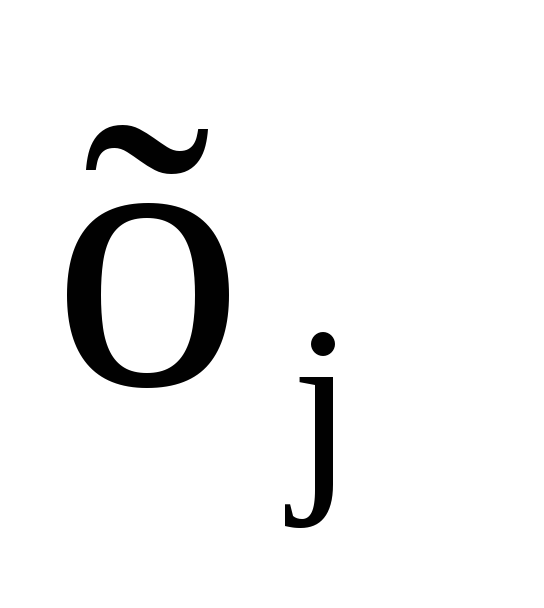
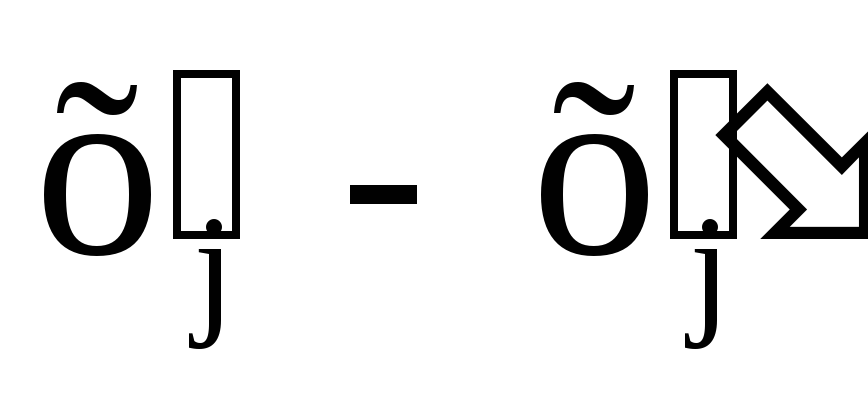
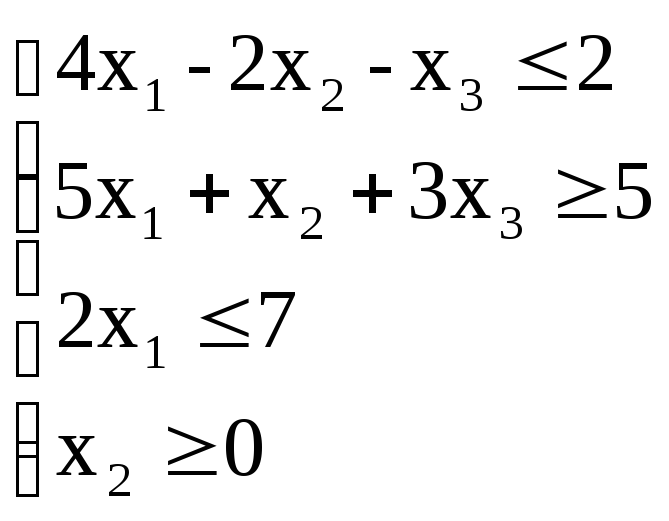
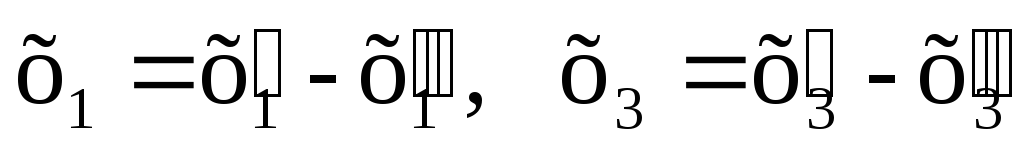
. Заменим такое ограничение следующими двумя ограничениями: 
где z— новая переменная, которая в целевую функцию вводится с коэффициентом 0 (иначе говоря, переменная z не вводится в целевую функцию). Значение переменной z можно не учитывать после решения новой задачи. Аналогично, ограничение вида 
заменяется двумя ограничениями: 
3) Предположим, что в ЗЛП не ко всем переменным предъявлено требование неотрицательности. Тогда каждую, переменную 
, на которую не наложено требование неотрицательности, представим в виде разности двух неотрицательных переменных: 
(2.6) Каждое вхождение переменной 
в целевую функцию или ограничения заменим разностью
. Решив новую задачу с помощью (2.6), вернемся к прежним переменным. Указанными приемами любая ЗЛП приводится к каноническому виду. Пример. Привести к каноническому виду 
Проделаем описанные действия. 
Теперь получим ЗЛП в каноническом виде: 
2.7. Понятие опорного плана злп.
Пусть ВЛП задана в каноническом виде (2.3 — 2.5). Предположим, что система уравнений (2.4) приведена к жордановой форме с неотрицательными правыми частями: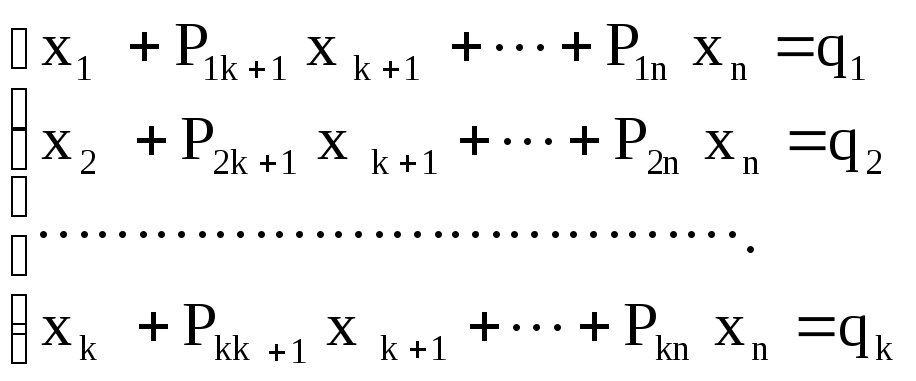 
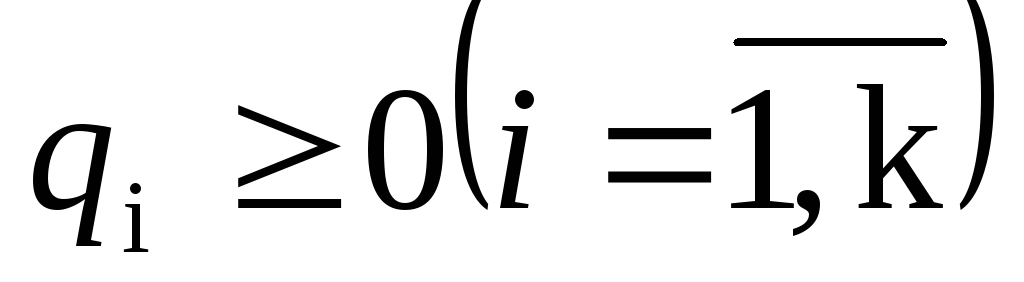
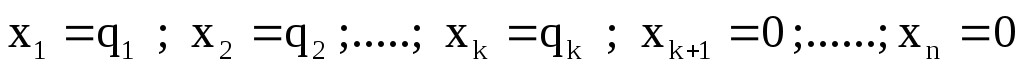
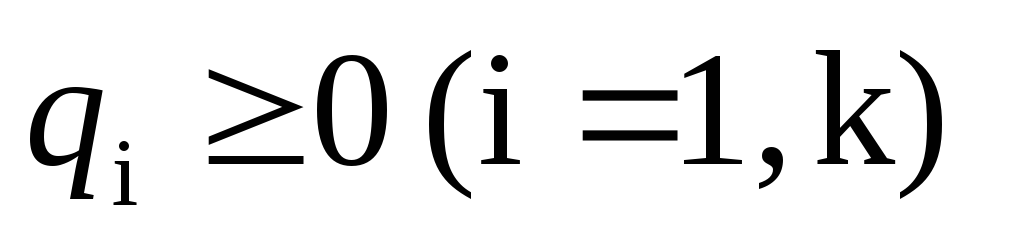
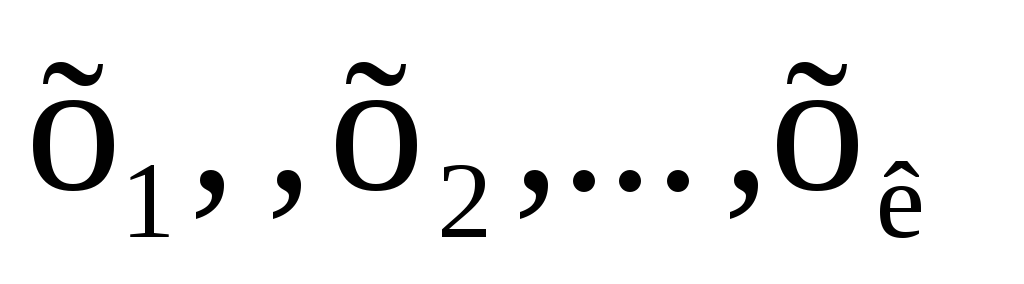
(2.6) где 
. Приравняв к нулю свободные переменные, получим базисное решение системы (2.4) 
(2.7) В силу условия 
набор значений переменных (2.7) удовлетворяет и ограничениям (2.5). Поэтому (2.6) являетсядопустимым решением ЗЛП. Допустимое решение (2.7) называется базисным допустимым решением или опорным планом ЗЛП. При этом говорят, что переменные 
образуют допустимый базис. Оказывается, что если ОДР изобразить геометрически, то каждый опорный план ЗЛП соответствует вершине многогранника. Поэтому справедлива следующая теорема. Если ЗЛП разрешима, то существует оптимальный опорный план.
3. Симплексный метод решения злп
3.1. Общая характеристика и основные этапы симплекс – метода
Основоположниками симплекс-метода являются советский математик Л.В. Канторович и американский математик Дж. Данциг. Симплекс-методом можно решить любую ЗЛП или обнаружить ее неразрешимость. Многие специальные классы ЗЛП можно решить другими, более эффективными для этих классов методами. Однако преимущество симплекс-метода — его универсальность. Почти для всех ЭВМ разработаны стандартные программы для решения ЗЛП симплекс — методом. Опишем общую идею симплекс-метода. Считаем, что ЗЛП записана в каноническом виде и целевую функцию нужно минимизировать. Как мы уже знаем, оптимальный план следует искать среди опорных планов ЗЛП. Симплекс-метод не перебирает все опорные планы (что было бы часто невозможно из-за их огромного количества), а, начиная с некоторого исходного опорного плана, он последовательно переходит к другим опорным планам с уменьшением целевой функции. Симплекс-метод прекращает свою работу тогда, когда либо будет найден оптимальный опорный план, либо установлена неразрешимость задачи. При решении ЗЛП симплекс-методом можно выделить следующие этапы: 1) приведение ЗЛП к каноническому виду; 2) приведение системы линейных уравнений к жордановой форме с неотрицательными правыми частями с одновременной проверкой на неразрешимость ЗЛП из-за противоречивости системы линейных ограничений; 3) исследование опорного плана на оптимальность; 4) исследование ЗЛП на неразрешимость из-за неограниченности снизу на ОДР целевой функции; 5) переход к новому, «лучшему» опорному плану.