Как работает linkage python

scipy.cluster.hierarchy.linkage#

The input y may be either a 1-D condensed distance matrix or a 2-D array of observation vectors.

If y is a 1-D condensed distance matrix, then y must be a \(\binom\) sized vector, where n is the number of original observations paired in the distance matrix. The behavior of this function is very similar to the MATLAB linkage function.

A \((n-1)\) by 4 matrix Z is returned. At the \(i\) -th iteration, clusters with indices Z[i, 0] and Z[i, 1] are combined to form cluster \(n + i\) . A cluster with an index less than \(n\) corresponds to one of the \(n\) original observations. The distance between clusters Z[i, 0] and Z[i, 1] is given by Z[i, 2] . The fourth value Z[i, 3] represents the number of original observations in the newly formed cluster.

The following linkage methods are used to compute the distance \(d(s, t)\) between two clusters \(s\) and \(t\) . The algorithm begins with a forest of clusters that have yet to be used in the hierarchy being formed. When two clusters \(s\) and \(t\) from this forest are combined into a single cluster \(u\) , \(s\) and \(t\) are removed from the forest, and \(u\) is added to the forest. When only one cluster remains in the forest, the algorithm stops, and this cluster becomes the root.

A distance matrix is maintained at each iteration. The d[i,j] entry corresponds to the distance between cluster \(i\) and \(j\) in the original forest.

At each iteration, the algorithm must update the distance matrix to reflect the distance of the newly formed cluster u with the remaining clusters in the forest.

Suppose there are \(|u|\) original observations \(u[0], \ldots, u[|u|-1]\) in cluster \(u\) and \(|v|\) original objects \(v[0], \ldots, v[|v|-1]\) in cluster \(v\) . Recall, \(s\) and \(t\) are combined to form cluster \(u\) . Let \(v\) be any remaining cluster in the forest that is not \(u\) .

The following are methods for calculating the distance between the newly formed cluster \(u\) and each \(v\) .

Warning: When the minimum distance pair in the forest is chosen, there may be two or more pairs with the same minimum distance. This implementation may choose a different minimum than the MATLAB version.

Parameters : y ndarray

A condensed distance matrix. A condensed distance matrix is a flat array containing the upper triangular of the distance matrix. This is the form that pdist returns. Alternatively, a collection of \(m\) observation vectors in \(n\) dimensions may be passed as an \(m\) by \(n\) array. All elements of the condensed distance matrix must be finite, i.e., no NaNs or infs.

method str, optional

The linkage algorithm to use. See the Linkage Methods section below for full descriptions.

metric str or function, optional

The distance metric to use in the case that y is a collection of observation vectors; ignored otherwise. See the pdist function for a list of valid distance metrics. A custom distance function can also be used.

optimal_ordering bool, optional

If True, the linkage matrix will be reordered so that the distance between successive leaves is minimal. This results in a more intuitive tree structure when the data are visualized. defaults to False, because this algorithm can be slow, particularly on large datasets [2]. See also the optimal_leaf_ordering function.

The hierarchical clustering encoded as a linkage matrix.

pairwise distance metrics

1. For method ‘single’, an optimized algorithm based on minimum spanning tree is implemented. It has time complexity \(O(n^2)\) . For methods ‘complete’, ‘average’, ‘weighted’ and ‘ward’, an algorithm called nearest-neighbors chain is implemented. It also has time complexity \(O(n^2)\) . For other methods, a naive algorithm is implemented with \(O(n^3)\) time complexity. All algorithms use \(O(n^2)\) memory. Refer to [1] for details about the algorithms.
2. Methods ‘centroid’, ‘median’, and ‘ward’ are correctly defined only if Euclidean pairwise metric is used. If y is passed as precomputed pairwise distances, then it is the user’s responsibility to assure that these distances are in fact Euclidean, otherwise the produced result will be incorrect.

Daniel Mullner, “Modern hierarchical, agglomerative clustering algorithms”, arXiv:1109.2378v1.

Ziv Bar-Joseph, David K. Gifford, Tommi S. Jaakkola, “Fast optimal leaf ordering for hierarchical clustering”, 2001. Bioinformatics DOI:10.1093/bioinformatics/17.suppl_1.S22

>>> from scipy.cluster.hierarchy import dendrogram, linkage >>> from matplotlib import pyplot as plt >>> X = [[i] for i in [2, 8, 0, 4, 1, 9, 9, 0]] 

>>> Z = linkage(X, 'ward') >>> fig = plt.figure(figsize=(25, 10)) >>> dn = dendrogram(Z) 

>>> Z = linkage(X, 'single') >>> fig = plt.figure(figsize=(25, 10)) >>> dn = dendrogram(Z) >>> plt.show() 

Источник

Hierarchical Clustering in Python, SciPy (with Example)

Hierarchical clustering is a machine learning algorithm often used in unsupervised learning for clustering problems.

In this tutorial, we will learn how the hierarchical clustering algorithms work and how to use Python and SciPy to group data into clusters as in the example below.

What is Hierarchical Clustering?

Hierarchical clustering, also known as hierarchical cluster analysis, is an unsupervised learning algorithm used to group similar objects into clusters.

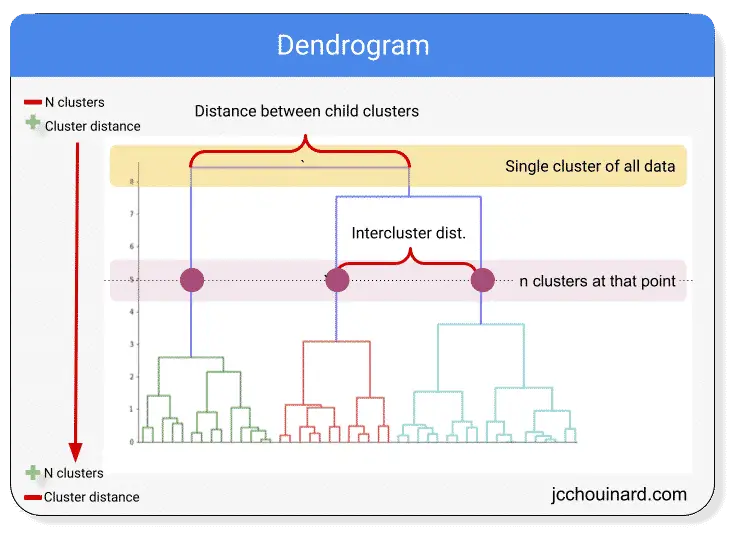
The image above shows a dendrogram.

The dendrogram can be used to visualize hierarchical clustering.

The algorithm starts by assigning 1 cluster for each data point (bottom of the graph).

It then merges the closest clusters at each iteration and ends with a single cluster for the entire dataset.

Pros and Cons of hierarchical clustering

Advantages

Can help for the discovery of the optimal number of clusters.

Insightful and interpretable data visualization

Disadvantages

Not scalable as runtime increases with the number of data points. Kmeans is significantly faster on large datasets.

How does Hierarchical Clustering Work?

1. Having 1 cluster for each data point
2. Defining new cluster centers using the mean of X and Y coordinates
3. Combining clusters centers closest to each other
4. Finding new cluster centers based on the mean
5. Repeating until optimal number of clusters is met

Hierarchical Clustering in SciPy

One common algorithm used for hierarchical cluster analysis is hierarchy from the scipy.cluster SciPy library.

linkage

The linkage method is used to create the clusters and is accessible here: scipy.cluster.hierarchy.linkage

# create clusters linkage( y, method='', metric='' )

• The input y may be either a 1-D condensed distance matrix or a 2-D array of observation vectors.
• method is used to define the statistical model to use to calculate the proximity of clusters
• metric is the distance between two objects.

fcluster

The fcluster method is used to predict labels on the data and is accessible here: scipy.cluster.hierarchy.fcluster

# Predict cluster labels fcluster( matrix, n_clusters, criterion='' )

• The input is a matrix returned by the linkage method.
• n_clusters depends on the chosen criterion
• criterion defines how to decide the thresholds to apply

SciPy Hierarchical cluster analysis in Python

Let’s use Python to create hierarchical clusters on dummy data generated with NumPy.

Seaborn and matplotlib will be used for data visualization and Pandas to combine the arrays into a dataframe.

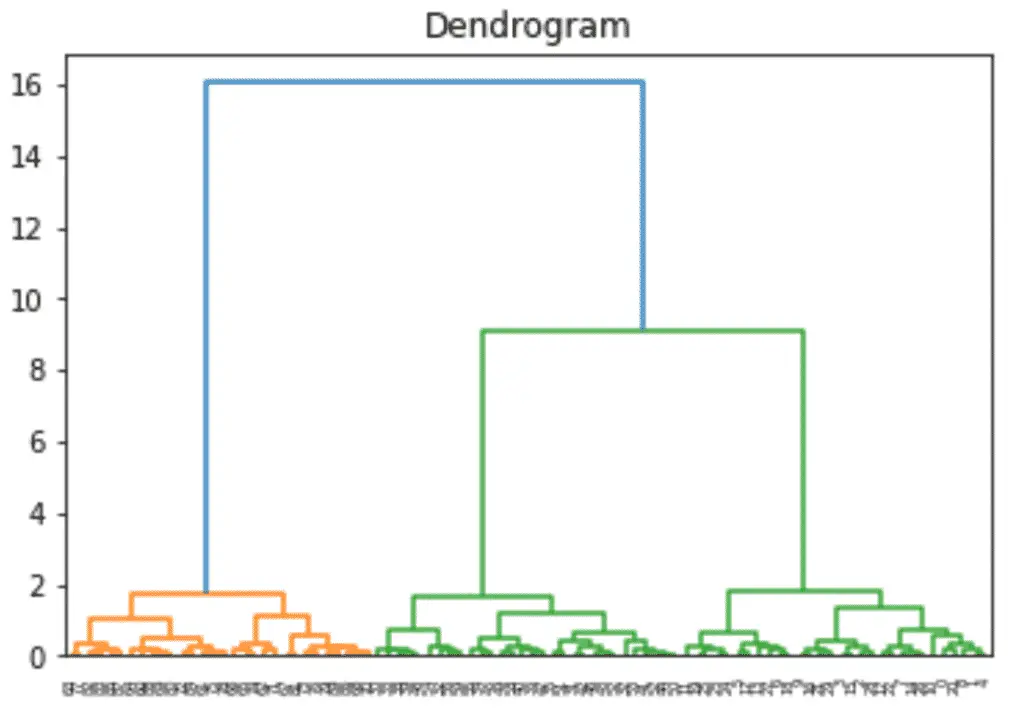
import matplotlib.pyplot as plt import numpy as np from numpy.random import rand import pandas as pd import seaborn as sns from scipy.cluster.vq import whiten from scipy.cluster.hierarchy import fcluster, linkage # Generate initial data data = np.vstack(( (rand(30,2)+1), (rand(30,2)+2.5), (rand(30,2)+4) )) # standardize (normalize) the features data = whiten(data) # Compute the distance matrix matrix = linkage( data, method='ward', metric='euclidean' ) # Assign cluster labels labels = fcluster( matrix, 3, criterion='maxclust' ) # Create DataFrame df = pd.DataFrame(data, columns=['x','y']) df['labels'] = labels # Plot Clusters sns.scatterplot( x='x', y='y', hue='labels', data=df ) plt.title('Hierachical Clustering with SciPy') plt.show()

Build a Dendrogram

from scipy.cluster.hierarchy import dendrogram dn = dendrogram(matrix) plt.title('Dendrogram') plt.show()

Interesting posts in the community

• Social Network Analysis through Hierarchical Clustering by Maksim Tsvetovat and Alexander Kouznetsov
• Document Clustering with Python by Brandon Rose
• Customer-segmentation for differentiated targeting in marketing using clustering analysis by Debayan Mitra
• K-Means clustering and hierarchical document clustering on the most popular Tweets of US congresspeople by Noah Segal-Gould and Tanner Cohan

Conclusion

We have now covered how hierarchical clustering works and how to group data into clusters using Python and SciPy.

It is an interesting way to cluster data into classes but has some pitfalls. I suggest that you read how to use the K-Means algorithms in Python when dealing with larger datasets.

Источник