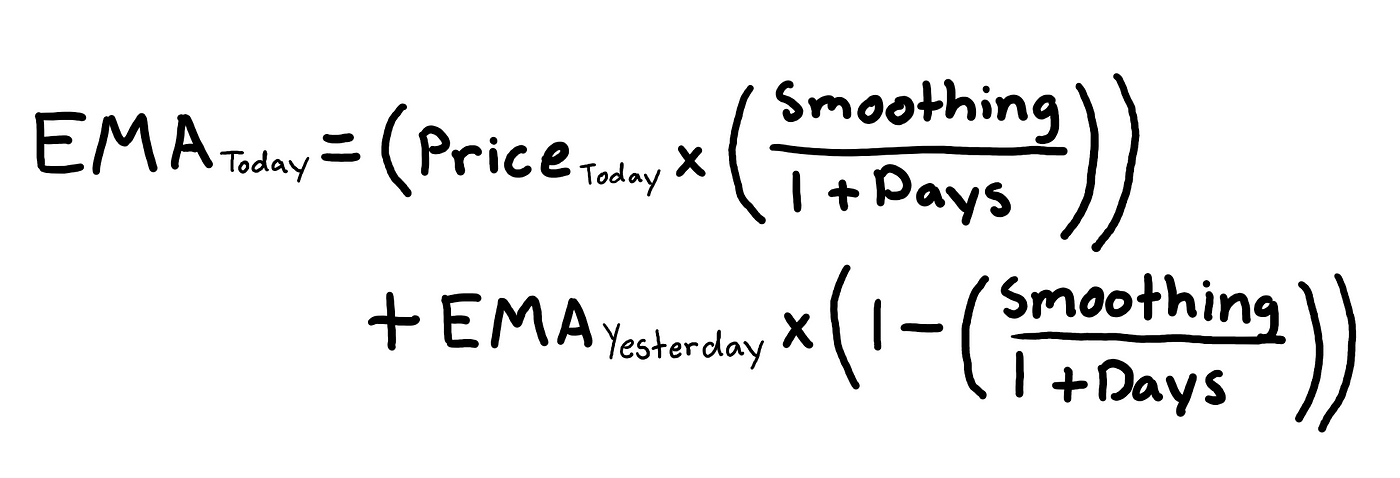- calculate exponential moving average in python
- 16 Answers 16
- How To Calculate The EMA Of A Stock With Python
- Step 1. Install the modules
- Step 2. Understanding Exponential Moving Average
- Step 3. How to calculate EMA
- Step 3.1. Example
- Step 4. Coding Setup
- Step 5. Calculating EMA
- Step 6. Plotting the results
- Conclusion. How to use EMA for stocks?
calculate exponential moving average in python
I have a range of dates and a measurement on each of those dates. I’d like to calculate an exponential moving average for each of the dates. Does anybody know how to do this? I’m new to python. It doesn’t appear that averages are built into the standard python library, which strikes me as a little odd. Maybe I’m not looking in the right place. So, given the following code, how could I calculate the moving weighted average of IQ points for calendar dates?
from datetime import date days = [date(2008,1,1), date(2008,1,2), date(2008,1,7)] IQ = [110, 105, 90] 16 Answers 16
EDIT: It seems that mov_average_expw() function from scikits.timeseries.lib.moving_funcs submodule from SciKits (add-on toolkits that complement SciPy) better suits the wording of your question.
To calculate an exponential smoothing of your data with a smoothing factor alpha (it is (1 — alpha) in Wikipedia’s terms):
>>> alpha = 0.5 >>> assert 0 < alpha >> av = sum(alpha**n.days * iq . for n, iq in map(lambda (day, iq), today=max(days): (today-day, iq), . sorted(zip(days, IQ), key=lambda p: p[0], reverse=True))) 95.0 The above is not pretty, so let’s refactor it a bit:
from collections import namedtuple from operator import itemgetter def smooth(iq_data, alpha=1, today=None): """Perform exponential smoothing with factor `alpha`. Time period is a day. Each time period the value of `iq` drops `alpha` times. The most recent data is the most valuable one. """ assert 0 < alpha $ python26 smooth.py IQData(date=datetime.date(2008, 1, 1), iq=110) IQData(date=datetime.date(2008, 1, 2), iq=105) IQData(date=datetime.date(2008, 1, 7), iq=90) 95.0 Hi J.F. Sebastian, I'd like to use this EWMA formula to show trends on my website. I've posted a question on SO — stackoverflow.com/questions/9283856. Someone suggested the EWMA algorithm for this as I need to stress more on recent items than older ones. Since I have no experience with stats, I'm a little confused as to how I calculate the value of α . Any help? Thank you.
I'm always calculating EMAs with Pandas:
Here is an example how to do it:
import pandas as pd import numpy as np def ema(values, period): values = np.array(values) return pd.ewma(values, span=period)[-1] values = [9, 5, 10, 16, 5] period = 5 print ema(values, period) More infos about Pandas EWMA:
@user3226167 no i thought that "alpha" is variable X, but then i found that the equation is already incorporated in the function and one just changes the static alpha parameter
def ema(s, n): """ returns an n period exponential moving average for the time series s s is a list ordered from oldest (index 0) to most recent (index -1) n is an integer returns a numeric array of the exponential moving average """ s = array(s) ema = [] j = 1 #get n sma first and calculate the next n period ema sma = sum(s[:n]) / n multiplier = 2 / float(1 + n) ema.append(sma) #EMA(current) = ( (Price(current) - EMA(prev) ) x Multiplier) + EMA(prev) ema.append(( (s[n] - sma) * multiplier) + sma) #now calculate the rest of the values for i in s[n+1:]: tmp = ( (i - ema[j]) * multiplier) + ema[j] j = j + 1 ema.append(tmp) return ema Why is the function using a local variable with the same name as the function? Apart from making the code slightly less legible, it could introduce hard to detect logical bugs further down the line .
@chjortlund I'm not sure what you mean by "every second item in the list will be the SMA". Current EMA value is based on previous one, but you have to start somewhere so SMA is taken as initial value of set. It's correct way to calculate EMA.
@Zuku True, I have deleted my comment. Back when I made it, I was looking for an algorithm to process live incoming data, and the above snippet is not suitable for that use case (nor is it advertised as) - my mistake!
You can also use the SciPy filter method because the EMA is an IIR filter. This will have the benefit of being approximately 64 times faster as measured on my system using timeit on large data sets when compared to the enumerate() approach.
import numpy as np from scipy.signal import lfilter x = np.random.normal(size=1234) alpha = .1 # smoothing coefficient zi = [x[0]] # seed the filter state with first value # filter can process blocks of continuous data if is maintained y, zi = lfilter([1.-alpha], [1., -alpha], x, zi=zi) I don't know Python, but for the averaging part, do you mean an exponentially decaying low-pass filter of the form
y_new = y_old + (input - y_old)*alpha where alpha = dt/tau, dt = the timestep of the filter, tau = the time constant of the filter? (the variable-timestep form of this is as follows, just clip dt/tau to not be more than 1.0)
y_new = y_old + (input - y_old)*dt/tau If you want to filter something like a date, make sure you convert to a floating-point quantity like # of seconds since Jan 1 1970.
My python is a little bit rusty (anyone can feel free to edit this code to make corrections, if I've messed up the syntax somehow), but here goes.
def movingAverageExponential(values, alpha, epsilon = 0): if not 0 < alpha < 1: raise ValueError("out of range, alpha='%s'" % alpha) if not 0 This function moves backward, from the end of the list to the beginning, calculating the exponential moving average for each value by working backward until the weight coefficient for an element is less than the given epsilon.
At the end of the function, it reverses the values before returning the list (so that they're in the correct order for the caller).
(SIDE NOTE: if I was using a language other than python, I'd create a full-size empty array first and then fill it backwards-order, so that I wouldn't have to reverse it at the end. But I don't think you can declare a big empty array in python. And in python lists, appending is much less expensive than prepending, which is why I built the list in reverse order. Please correct me if I'm wrong.)
The 'alpha' argument is the decay factor on each iteration. For example, if you used an alpha of 0.5, then today's moving average value would be composed of the following weighted values:
today: 1.0 yesterday: 0.5 2 days ago: 0.25 3 days ago: 0.125 . etc. Of course, if you've got a huge array of values, the values from ten or fifteen days ago won't contribute very much to today's weighted average. The 'epsilon' argument lets you set a cutoff point, below which you will cease to care about old values (since their contribution to today's value will be insignificant).
You'd invoke the function something like this:
result = movingAverageExponential(values, 0.75, 0.0001) How To Calculate The EMA Of A Stock With Python
In this article, I will be showing you how you can calculate the Exponential Moving Average of a stock using Python.
Step 1. Install the modules
The modules that we will be needing are listed below and you can simply install them with a pip3 install .
pip3 install numpy==1.20.0\ pip3 install pandas==1.1.4\ pip3 install pandas-datareader==0.9.0\ pip3 install matplotlib==3.3.3 Step 2. Understanding Exponential Moving Average
Although I won't be going too deep into the concept of EMA (Exponential Moving Average), I will be giving you a brief overview of what it is. EMA is a type of moving average indicator that gives greater weight or importance to previous stock prices. The essential difference between EMA and SMA is that EMA responds faster to upward price movement compared to SMA. The formula for calculating EMA is as follows.
The smoothing factor can be altered upon preference, but a common choice for this variable is 2 and that is what we will be using. Traders use various day lengths when calculating EMA, but a common one is a 10-day period and that is what we will be using.
Step 3. How to calculate EMA
In Step 2, we established that we would be calculating EMA for every 10 day observations. The first step to calculating EMA is to actually calculate the SMA of the day length constant. In our case, we will first calculate the SMA of the first 10 stock prices. We will then consider the 10 day SMA to be our first EMA value. Now we will calculate the EMA for the 11th day price using the formula I mentioned earlier. You can repeat the process of using the EMA formula repeatedly until you have finished calculating for all the stock prices.
Step 3.1. Example
In this example, we will be calculating the 5-day EMA of the following set of numbers with a smoothing value of 2.
10, 11, 11.5, 10.75, 12, 11.75, 12.25, 14, 16, 17, 15.6, 15.75, 16, 14, 16.5, 17, 17.25, 18, 18.75, 20 The first thing we will do is find the SMA of the first 5 numbers.
EMA = []\ (10 + 11 + 11.5 + 10.75 + 12) / 5 = 11.05 Let's add 11.05 to our EMA list.
Now we will use the EMA formula to calculate the EMA for the 6th number.
(11.75 x (2 / (1 + 5))) + 11.05 x (1 - (2 / (1 + 5))) = 11.28\ Add 11.28 to our list of EMA: [11.05, 11.28] Continue the process of using the EMA formula for all the numbers in the set and that is how you calculate the EMA of a stock.
11.05, 11.28, 11.61, 12.40, 13.60, 14.73, 15.02, 15.26, 15.51, 15.01, 15.50, 16.00, 16.42, 16.95, 17.55, 18.36 Step 4. Coding Setup
Now its time to start coding. We can start by setting up the basic things we will need.
- Import all the necessary modules
- Create an empty function calculate_ema(prices, days, smoothing=2)
- Get the stock price data for a certain stock - (MSFT, 2015--01--01, 2016--01--01)
import numpy as np import pandas as pd import matplotlib.pyplot as plt import pandas_datareader as web def calculate_ema(prices, days, smoothing=2): pass symbol = 'MSFT' df = web.DataReader(symbol, 'yahoo', '2015-01-01', '2016-01-01') Step 5. Calculating EMA
Remember that the first step to calculating the EMA of a set of number is to find the SMA of the first numbers in the day length constant. There are two simple ways we can go about this.
def calculate_ema(prices, days, smoothing=2): ema = [sum(prices[:days]) / days] # First method ################################################ ema = [] ema.append(sum(prices[:days]) / days) # Second method Now we need to loop through the numbers that are not in the range of the day length constant and repeatedly calculate the EMA for them and add them to our EMA list.
def calculate_ema(prices, days, smoothing=2): ema = [sum(prices[:days]) / days] for price in prices[days:]: ema.append((price * (smoothing / (1 + days))) + ema[-1] * (1 - (smoothing / (1 + days)))) return ema By the end of this step, your code should look something like this.
import numpy as np import pandas as pd import matplotlib.pyplot as plt import pandas_datareader as web def calculate_ema(prices, days, smoothing=2): ema = [sum(prices[:days]) / days] for price in prices[days:]: ema.append((price * (smoothing / (1 + days))) + ema[-1] * (1 - (smoothing / (1 + days)))) return ema symbol = 'MSFT' df = web.DataReader(symbol, 'yahoo', '2015-01-01', '2016-01-01') ema = calculate_ema(df['Close'], 10) # Add this line to save EMA values in a list Step 6. Plotting the results
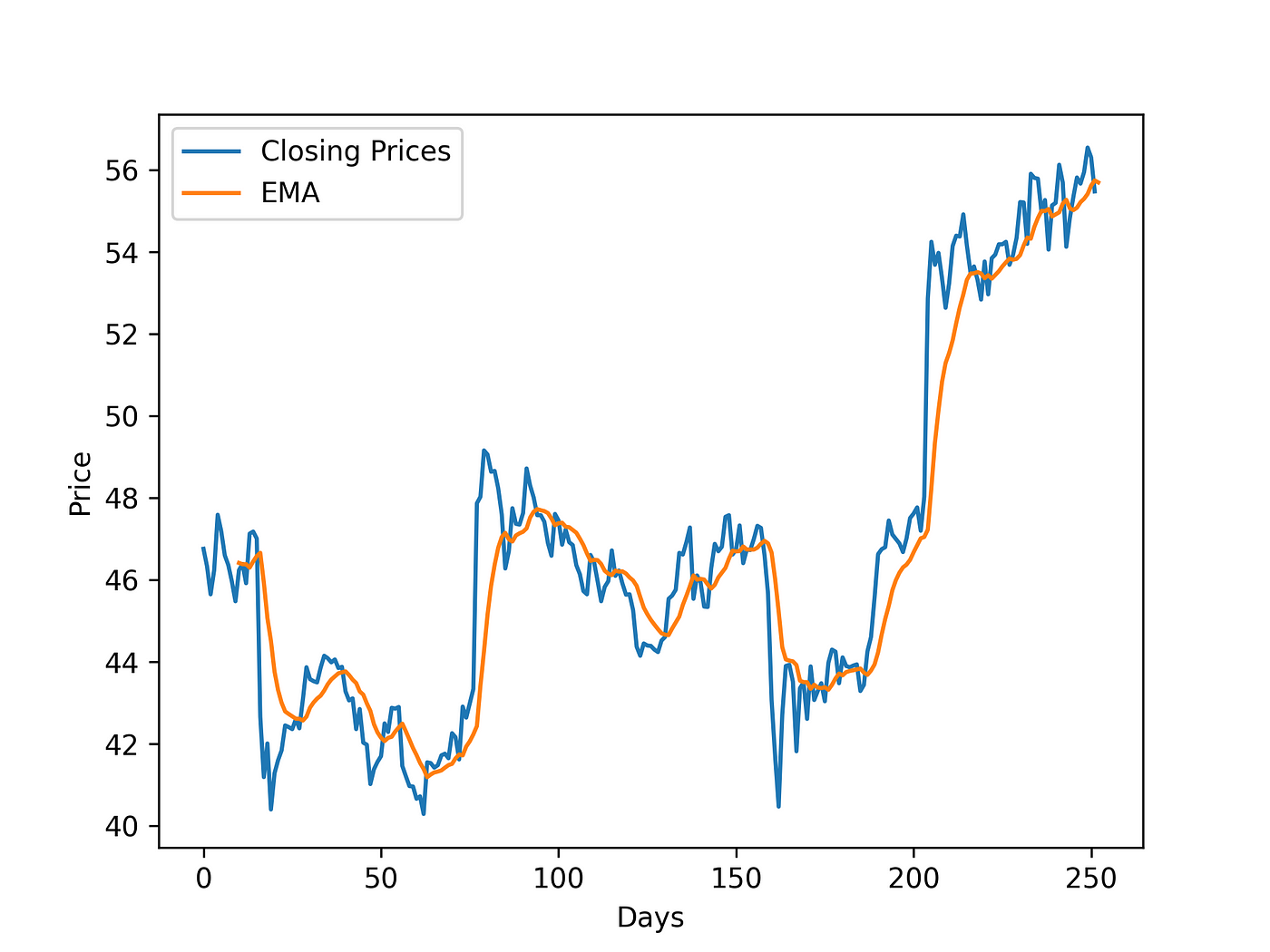
We can plot the actual stock prices and the calculated EMA with matplotlib.
import numpy as np import pandas as pd import matplotlib.pyplot as plt import pandas_datareader as web def calculate_ema(prices, days, smoothing=2): ema = [sum(prices[:days]) / days] for price in prices[days:]: ema.append((price * (smoothing / (1 + days))) + ema[-1] * (1 - (smoothing / (1 + days)))) return ema symbol = 'MSFT' df = web.DataReader(symbol, 'yahoo', '2015-01-01', '2016-01-01') ema = calculate_ema(df['Close'], 10) price_X = np.arange(df.shape[0]) # Creates array [0, 1, 2, 3, . df.shape[0]] ema_X = np.arange(10, df.shape[0]+1) # Creates array [10, 11, 12, 13, . df.shape[0]+1] # We start at 10, because we use the first 10 values to calculate the SMA, # then we calculate EMA form the 11th value plt.xlabel('Days') plt.ylabel('Price') plt.plot(price_X, df['Close'], label='Closing Prices') plt.plot(ema_X, ema, label='EMA') plt.legend() plt.show() Your plot should look something like this.
Conclusion. How to use EMA for stocks?
While there are many ways to use the Exponential Moving Average of a stock for technical analysis, a basic usage of it is recognizing a buy signal when the EMA line goes underneath and stock line and is heading in an upward direction. A sell signal can be recognized when the EMA line goes over the stock line and it is heading in a downward direction. To conclude, I hope you learned something new and useful from this article which you can use later in your Python projects.