Javascript dec to bin

How to Convert a Decimal to Binary in JavaScript

There are 10 kinds of programmers in the world: those who can convert decimal to binary and those who can’t. In this tutorial, you will learn how to convert a decmial to binary using a Stack data structure with examples in JavaScript.

Reflection Practice

What’s a Stack?

A stack is a data structure that follows the Last In First Out principle (LIFO). We can only add or remove elements from the top of the stack .

If you want to go deeper, read my article about the JavaScript Stack Data Structure.

What’s a Base?

A base is the number of different digits used to count in a numerical system. We count in base 10 most likely due to us evolving ten fingers. When we count in base 10, we use ten distinct whole numbers.

What is Binary?

Binary is base 2. We have two different digits to count with, 0 and 1 . (Or true and false ).

Counting from 1 to 10 with our hands is easy. Our fingers are like switches and we flip them.

(Starting with the index or thumb! Sheesh!)

What do we do when we go beyond 10?

We flip those switches the other way!

We not only extend or retract our fingers to count to ten, if we are counting to a value greater than ten, we also track the number of times we count by 10.

What happens when we reach 9?

We overflow into another digit on the left and reset the digit on the right, giving us 10 . We then increment the right-most digit as we count up:

10 11 12 13 14 15 16 17 18 19

What happens when we reach 19?

We increment the value of the digit on the left by 1 .

This may seem rudimentary, but bear with me.

What happens when we reach 99?

We need to overflow again and add another digit, giving us 100 .

If we knew at the outset that we wanted to count beyond 100 , we could start with three digits and proceed like this:

000 001 002 . 009 010 011 . 099 100 101

What if we are limited to two fingers, or switches?

We’re going to need a lot more digits!

Let’s Get Meta

• How do you build something out of nothing?
• What mathematical operation do we use to break problems down?
• What does the modulo operator do?

How to Convert Decimal to Binary

Our challenge is to convert a decimal, such as 10 , to its binary counterpart, 1010 .

How do we break this problem down?

It is one of ten possible values, or, 1 / 10 .

What mathematical operation do we use to break problems down?

It is one of two possible values.

If we’re using division to convert to binary, what is our divisor?

What does the operation of division return?

A quotient and a remainder.

Let’s start simple and convert 0 to binary. What is the quotient of the following:

What’s the remainder of 0 / 2 ? Also 0 .

If we start to build a table, it looks like this so far:

Because we are only working with two values, 0 and 1 , we can surmise that the decimal 1 converted to binary is also 1 .

But don’t take my word for it! Let’s proove it . What is 1 / 2 ?

Not exactly a whole number!

But the remainder is 1. How?

We use the division algorithm, which states that:

For integers N and D where D != 0 , there are unique integers Q and R where 0

Where N is our dividend, D is our divisor, and Q and R are the quotient and remainder, respectively.

👆 Keep in mind that Q is not the quotient we return from the division operation of 1 / 2 . It’s the number of times the divisor goes into the dividend, which is 0 .

So, using our equation above:

Another way to think about it is to calculate the division of 1 / 2 by hand.

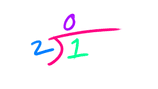
We add this value to our table:

Decimal	Binary
0	0
1	1
2	?

The quotient is 1 and the remainder is 0 . But we already have 1 and 0 in our table?

We need to overflow, meaning we now need at least two digits to represent anything greater than decimal 2 .

What happens when we overflow?

We increment the value to the left and reset the value on the right, so when we add 2 to our table:

Decimal	Binary
0	0
1	1
2	10

Are you starting to see the pattern?

We’re building our binary strings with the remainder, and not the quotient, of our division operation.

So the binary conversion of 2 is 10 .

You guessed it, we need to overflow.

Decimal	Binary
0	0
1	1
2	10
3	11
4	100

What about 5 ? Now its’ getting interesting. Our plan is to use a Stack data structure to in our algorithm solution. Using the LIFO principle, imagine pushing values to the binary string as we build it.

We push the remainder to a string:

We now divide our quotient, 2 , by 2 .

We push the remainder to our string:

We’re not at zero, yet. Our quotient is 1 , so we divide that by 2.

Our remainder is again 1 , so we push that to our string:

There’s our binary conversion of the decimal 5:

Decimal	Binary
0	0
1	1
2	10
3	11
4	100
5	101

How To Convert a Decimal to Binary Using a Stack in JavaScript

Let’s translate this to JavaScript using a Stack. If you’re unfamiliar with stacks, you may want to first read JavaScript Stack Data Structure.

const decimalToBinary = (num) =>  const stack = new Stack(); let result = ''; while (num > 0) stack.push(num % 2); num = Math.floor(num / 2); > while (stack.top > 0) result += stack.pop(); > return result; >

We first declare a new instance of our Stack class, stack .

We next declare a result variables, setting the value to an empty string.

We next declare two while loops.

The first while loop iterates over the value of our algorithm parameter, num . In each iteration, we use the modulo operator, % , to get the remainder of num divided by 2 and push() it to the stack . We then reassign the value of num to the current value of num divided by 2 . But! We use floor() to round it down. Why? We want to work with whole numbers and we are most interested in our remainder.

Let’s walk through each iteration.

If num is equal to 6 , then in our first iteration, we push 0 to the stack:

In the next iteration, num is now equal to 3 , so we push 1 to the stack:

The value of num is now 1 , which is greater than zero, so in the next iteration we push 1 to the stack:

The value of num is now less than zero, so we move on to the second while loop, which iterates over the stack. We use the pop() method to remove each value from the top of the stack and build our result string.

If we don’t want to use a Stack, we could simply concatenate a string, then reverse it:

const decimalToBinary = (num) =>  let result = ''; while (num > 0) result += num % 2; num = Math.floor(num / 2); > return result.split('').reverse().join(''); >

But the split() converts the string to an array, so we could just start with an array instead and use unshift() rather than reverse() (J4F):

const decimalToBinary = (num) =>  let result = []; while (num > 0) result.unshift(num % 2); num = Math.floor(num / 2); > return result.join(''); >

Or we could just cheat and use the built-in toString() method and pass it 2 as an argument, meaning we want to convert our string to binary:

const decimalToBinary = num => num.toString(2);

Reflection

• How do you build something out of nothing?
• What mathematical operation do we use to break problems down?
• What does the modulo operator do?

How Do You Build Something Out of Nothing?

What Mathematical Operation Do We Use to Break Problems Down?

Division! One of the keys to effective problem solving is breaking problems down into smaller problems. Here, we literally divided the problem.

What Does the Module Operator Do?

The modulo operator, % , returns the remainder of division, rather than the quotient.

In this tutorial, you learned how to convert a decmial to binary using a Stack data structure with examples in JavaScript.

Want to level up your problem solving skills? I write a bi-weekly newsletter about programming, problem solving and lifelong learning. Join now

Источник

Convert Decimal to Binary

A binary number is a number expressed in base-2, as opposed to conventional decimal numbers in base-10.

Below is a live calculator.

How the Calculator Works

Converting decimal numbers to binary in JavaScript is easy. For example, let x = 42 creates a new variable x that contains the base 10 number 42 . JavaScript numbers have a toString() method that takes a radix parameter. Calling x.toString(2) tells JavaScript to convert x to a string containing the binary representation of 42 .

let x = 42; x.toString(2); // '101010'

The toString() method also handles non-integers and negative numbers. For example:

x = 3.14; x.toString(2); // '11.001000111101011100001010001111010111000010100011111' x = -7; x.string(2); // '-111'

Mental Math

How do you quickly convert 7 to 111 in your head? It takes some practice to make it easy, but here’s the procedure to convert a positive integer v to a binary string:

• Start with an empty string
• Take v modulo 2 and add it to the end of the string
• Repeat with Math.floor(v / 2) until you get to 0 or 1

Below is a JavaScript function that implements the above procedure:

function toBinary(v, str) < if (!Number.isSafeInteger(v) || v < 0) < throw new Error('v must be a non-negative integer'); > if (v === 1) < return '1'; > if (v === 0) < return '0'; > return toBinary(Math.floor(v / 2)) + (v % 2); >

Here’s what the procedure looks like with 42:

1. 42 % 2 === 0 , ‘0’
2. 21 % 2 === 1 , ’10’
3. 10 % 2 === 0 , ‘010’
4. 5 % 2 === 1 , ‘1010’
5. 2 % 2 === 0 , ‘01010’
6. 1 , ‘101010’

More Fundamentals Tutorials

Источник

Convert a Number to Binary Format in JavaScript

1. Create a Function to Convert the Number to Binary in JavaScript
2. Convert a Number to Binary With toString(2) Function

Converting a number to binary is quite a complex process. If we are to sit and convert the numbers manually, the result will be error-prone. How do we change a number to a binary format? JavaScript does not have many built-in functions to do so. We will introduce how to convert a number to binary in JavaScript.

Create a Function to Convert the Number to Binary in JavaScript

Before we go to the code, we need to know the conversion process from a decimal number (base 10) to a binary number (base 2). For simplicity, we will cover the conversion of positive whole numbers in this article. Hence, the change of negative integers and floating-point numbers is out of the scope of this article.

Understand the Conversion Process

Given an integer (or JavaScript number), we keep dividing the number by two and capturing its remainder till the number turns less than 2. For example, if we have a number 25, keep dividing 25 by 2 until we get the quotient less than 2.

We read the digits from highest to lowest. Hence the binary value for number 25 is 1101.

We use the following set of calculations to confirm whether the binary value represents the correct decimal number. Each bit represented in the binary number is multiplied by 2 to power the bit position value (starting from 0).

= 2^4*(1) + 2^3*(1) + 2^2*(0) + 2^1*(0) + 2^0*(1) = 16 + 8 + 0 + 0 + 1 = 25 

JavaScript Code to Convert Number Into Its Binary Format

We build the following code on the method discussed above. The function convertToBinary1 consoles the binary equivalent of a decimal number passed as a parameter. Note that we read the result backward. Hence the code has been created considering all the afore-said factors in mind.

Using Iteration

function convertToBinary1 (number)   let num = number;  let binary = (num % 2).toString();  for (; num > 1; )   num = parseInt(num / 2);  binary = (num % 2) + (binary);  >  console.log(binary); >  window.onload = function ()   console.log(convertToBinary1(25));  console.log(convertToBinary1(8)); > 

Steps

Make a copy of the parameter passed to the function and store it in a temporary variable num .

Create a variable to store the binary bits. It essentially is of type string to make handling easier.

Start the iteration for generating the binary bits and let it continue till the number is no more divisible by 2.

In each iteration, we divide the number by 2 to get the quotient. We calculate the modulous of the quotient. This step generates the binary bits as modulous of a number with 2 generates the binary bits 0 or 1 .

Источник