Java sqrt negative number

Java Math sqrt()

The sqrt() method returns the square root of the specified number.

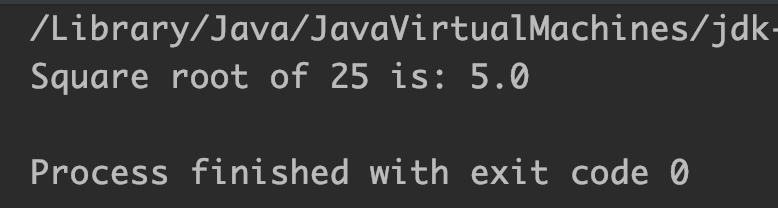
Example

class Main < public static void main(String[] args) < 
// compute square root of 25 System.out.println(Math.sqrt(25));
 > > // Output: 5.0

Syntax of Math.sqrt()

The syntax of the sqrt() method is:

Here, sqrt() is a static method. Hence, we are accessing the method using the class name, Math .

sqrt() Parameters

The sqrt() method takes a single parameter.

sqrt() Return Values

• returns square root of the specified number
• returns NaN if the argument less than 0 or NaN

Note: The method always returns the positive and correctly rounded number.

Example: Java Math sqrt()

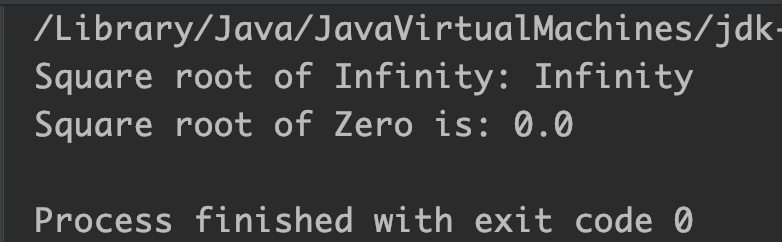
class Main < public static void main(String[] args) < // create a double variable double value1 = Double.POSITIVE_INFINITY; double value2 = 25.0; double value3 = -16; double value4 = 0.0; // square root of infinity 
System.out.println(Math.sqrt(value1)); // Infinity
 // square root of a positive number 
System.out.println(Math.sqrt(value2)); // 5.0
 // square root of a negative number 
System.out.println(Math.sqrt(value3)); // NaN
 // square root of zero 
System.out.println(Math.sqrt(value4)); // 0.0
 > >

In the above example, we have used the Math.sqrt() method to compute the square root of infinity, positive number, negative number, and zero.

Here, Double.POSITIVE_INFINITY is used to implement positive infinity in the program.

When we pass an int value to the sqrt() method, it automatically converts the int value to the double value.

int a = 36; Math.sqrt(a); // returns 6.0

Recommended Tutorials

Источник

Java Math.sqrt() Method

Java Math.sqrt() method returns the square root of a given number. In this guide, we will discuss sqrt() method in detail with examples.

Syntax of Math.sqrt() method

sqrt() Description

public static double sqrt(double num): Returns the square root of the given number num .

sqrt() Parameters

It takes a single parameter:

sqrt() Return Values

• Returns a double value, which is a square root of the given number.
• If the passed number is less than zero or NaN (Not a number) then this method returns NaN.
• If the passed argument is positive infinity, it returns positive infinity as square root.
• If the passed argument is zero, it returns zero.

Example 1: Finding Square root of a given number

Example 2: Square root of negative number and NaN

Example 3: Square root of zero

Recommended Posts

Top Related Articles:

About the Author

I have 15 years of experience in the IT industry, working with renowned multinational corporations. Additionally, I have dedicated over a decade to teaching, allowing me to refine my skills in delivering information in a simple and easily understandable manner.

Источник

Program to Find Square and Square Root in Java

Squares are the numbers generated when a value is multiplied by itself.

In contrast, a number’s square root is a value that, when multiplied by itself, returns the original value. Both are therefore vice-versa methods.

For example, the square of 3 3 3 is 9 9 9 and the square root of 9 9 9 is 3 3 3 .

In Java Math. sqrt() returns the square root of a value of type double passed to it as argument.(There are other ways as well)

As a programmer, I always find it fascinating to write programs for mathematical operations that I used to do by hand back in school.

Square and square root of a number is one of the principles which are used in many real-life applications as well as programming concepts. For example prime factors of a number, binary exponentiation etc.

Let’s start by defining what a square and square root actually means.

What is Square?

Simply put, the square of a number is the number multiplied by itself.

Square of X = X ∗ X X = X * X X = X ∗ X

For example, if X = 3 X = 3 X = 3

Square of 3 = 3 ∗ 3 = 9 3 = 3 * 3 = 9 3 = 3 ∗ 3 = 9

What is Square Root?

Square root is exactly the opposite of the square of a number. The square root of a number X is the number that when multiplied by itself equals X.

where √ is the symbol for square root

The square root of X can also be represented by X 1 / 2 X^ X 1 / 2 .

In a nutshell, if the square of a number X is S, then X is the square root of S.

Now that we know what we mean by the square and square root of a number, let’s see how we can write a program for square root in java.

How to square a number in Java?

There are a couple of ways to find the square of a number in Java. Let’s look at them one by one.

1. Multiplying the number by itself

It’s as simple as it sounds. Just multiply the number by itself and you’re good to go.

2. Using Math.pow Method

Math is a utility class in Java that has many useful mathematical functions, one of which is pow which allows you to calculate the exponentiation or power of a number.

Syntax:

Parameters : base, exponent Returns: base to the power of exponent

Both parameters accept double as the input. The return type is also a double value.

If you pass an integer or any primitive numerical value to either base or exponent, it will automatically be cast to double in Java.

So, if base = 10, exponent = 2 Math.pow(10, 2) = 100.0

So, in order to find the square of a number, we can pass the base as the number and the exponent as 2. Here’s a snippet that shows the usage of Math.pow .

How to find Square Root in Java?

Calculating the square of a number was pretty straightforward right. But calculating the Square Root in Java is a bit more interesting. Let’s see how we can do that.

1. Square Root in Java Using Math.sqrt()

This is the friendly sibling of the Math.pow function we saw in the previous segment. Like the way it reads, it finds the square root of a number.

Syntax

Parameters : number Returns: The square root of number

The number parameter accepts double as input and the return type is also a double value.

So, if number = 9 Math.sqrt(9) = 3.0

Here’s a snippet that demonstrates the use of Math.sqrt()

2. Square Root in Java Using Math.pow()

Just like we used Math.pow to find the square of a number, we can use it to find the square root of a number as well.

Remember the way the square root of a number is represented: X 1 / 2 X^ X 1 / 2 ; it means the square root of a number is X to the power of ½.

So if we pass the value of the exponent in Math.pow as 0 . 5 0.5 0 . 5 which is KaTeX parse error: Expected ‘EOF’, got ‘½’ at position 1: ½̲ , the resulting number will be the square root. Let’s try that in the below snippet.

Neat right? The same function is used to calculate two different operations.

3. Square Root in Java Without using any inbuilt function

Now that we have looked at a few ways to find the square root of a number using inbuilt functions in Java, let’s look at a way without using any such inbuilt function.

Let me propose an algorithm first, and then we’ll break it down one step at a time.

1. Start from i = 1 i = 1 i = 1 , if i ∗ i = = n i * i == n i ∗ i = = n , then i is the square root of n as n is a perfect square.
2. if i ∗ i > n i * i > n i ∗ i > n , it means the square root must lie between ( i − 1 , i ) (i-1, i) ( i − 1 , i ) , let’s call them ( l o w , h i g h ) (low, high) ( l o w , h i g h ) .
3. Apply binary search in the range ( l o w , h i g h ) (low, high) ( l o w , h i g h ) . Find m i d mid m i d of ( l o w , h i g h ) (low, high) ( l o w , h i g h ) :
4. if m i d ∗ m i d = = n mid * mid == n m i d ∗ m i d = = n , it means we assume that m i d mid m i d is the square root of n n n .
5. if m i d ∗ m i d > n mid * mid > n m i d ∗ m i d > n , it means that the assumption we made is incorrect. This implies, the square root of n must be less than mid since any value higher than mid can never satisfy the condition m i d ∗ m i d = = n mid * mid == n m i d ∗ m i d = = n . Hence, we will try to find the square root on the left side of mid by repeating step 3 for ( l o w , m i d ) (low, mid) ( l o w , m i d ) .
6. Otherwise, m i d ∗ m i d < n mid * mid < n m i d ∗ m i d < n means that our assumption is incorrect. It implies the square root of n n n must be greater than mid since any value less than mid can never satisfy the condition m i d ∗ m i d = = n mid * mid == n m i d ∗ m i d = = n . Hence, we will try to find the square root on the right side of m i d mid m i d by repeating step 3 for ( m i d , h i g h ) (mid, high) ( m i d , h i g h ) .

What is Perfect Square?

A perfect square is an integer that is the square of an integer. For example,

X = 9 = 3 ∗ 3 = 3 2 X = 9 = 3 * 3 = 3^ X = 9 = 3 ∗ 3 = 3 2

Here, 9 is a perfect square because 9 9 9 is the square of 3 3 3 . On the other hand, 1 0 10 1 0 is not a perfect square because it cannot be represented as the square of an integer.

So, if we want to calculate the square root of X X X , which is a perfect square, we need to find a number that, when multiplied by itself, equals X X X .

Numbers that are not a perfect square will have a real number (decimal) as their square root. So, we need a way to find the nearest approximate value for the square root (up to 6 decimal places for now). It’ll be something like: R.abcdef

Let’s say we need to find the square root of 1 3 13 1 3 , which is not a perfect square. Let’s find R first.

Observe that the maximum perfect square less than 1 3 13 1 3 is 9 9 9 whose square root is 3 3 3 . Since the square of 4 4 4 is 1 6 16 1 6 , which is greater than 1 3 13 1 3 , the square root of 1 3 13 1 3 has to be less than 4 4 4 . So we can be sure that the square root of 1 3 13 1 3 as well will be something like 3 . a b c d e f 3.abcdef 3 . a b c d e f .

Now that we have the value of R ( 3 ) R(3) R ( 3 ) let’s find abcdef.

In order to find the decimal places, we can use Binary Search. We know that the square root will lie between ( 3 3 3 , 4 4 4 ). We apply binary search in this range to find the value whose square is equal to 1 3 13 1 3 (up to 6 6 6 decimal places). Here is a sample walkthrough of how we are applying binary search.

Hence, the square root of 1 3 = 3 . 6 0 5 5 5 1 13 = 3.605551 1 3 = 3 . 6 0 5 5 5 1

Here is a snippet of this algorithm

Conclusion

• Squares are the numbers generated after multiplying a value by itself. In contrast, the square root of a number is a value which, on getting multiplied by itself, gives the original value.
• We can square a number in Java in two different ways, multiplying the number by itself and calling the Math.pow function.
• We can find sqaure root in Java by using Math.sqrt function, using Math.pow function, or calculating it using a binary search for the given range.
• A perfect square is an integer that is the square of an integer.

Exercise

• What will happen if a negative number is passed as the exponent parameter to the Math.pow function?
• What will happen if a negative number is passed to the Math.sqrt function?
• Can you think of improving the time complexity of the binary search algorithm we used above to find the square root of a number?

See More

Источник