Java обход дерева пример

Поиск в ширину (BFS) и поиск в глубину (DFS) для двоичных деревьев в Java

Поиск в ширину и поиск в глубину — это два метода обхода графов и деревьев. В этом руководстве мы сосредоточимся в основном на обходах BFS и DFS в деревьях.

Что такое поиск в глубину (DFS)?

Алгоритм начинается с корневого узла, а затем исследует каждую ветвь перед возвратом. Он реализован с помощью стеков. Часто при написании кода мы используем стеки рекурсии для возврата. Используя рекурсию, мы можем воспользоваться тем фактом, что левое и правое поддеревья также являются деревьями и имеют одни и те же свойства.

Для двоичных деревьев существует три типа обхода DFS.

Что такое поиск в ширину (BFS)?

Этот алгоритм также начинается с корневого узла, а затем посещает все узлы уровень за уровнем. Это означает, что после корня он проходит по всем прямым дочерним элементам корня. После обхода всех прямых потомков корня он переходит к их потомкам и так далее. Для реализации BFS мы используем очередь.

Для бинарных деревьев у нас есть обход порядка уровней, который следует за BFS.

Реализация BFS и DFS на Java

Пусть рассматриваемое дерево:

Структура класса TreeNode выглядит следующим образом:

1. Обход предварительного заказа

При предварительном обходе бинарного дерева мы сначала обходим корень, затем левое поддерево и, наконец, правое поддерево. Мы делаем это рекурсивно, чтобы воспользоваться тем фактом, что левое и правое поддеревья также являются деревьями.

Алгоритм обхода предварительного заказа следующий:

1. Обход корня.
2. Вызов preorder() для левого поддерева.
3. Вызов preorder() для правого поддерева.

Обход предварительного заказа дерева выше:

Java-код выглядит следующим образом:

 static void preorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse root System.out.print(TreeNode.item + "->"); // Traverse left preorder(TreeNode.left); // Traverse right preorder(TreeNode.right); > 

2. Обход по порядку

Обход двоичного дерева по порядку сначала проходит через левое поддерево, затем корень и, наконец, правое поддерево.

Алгоритм обхода по порядку следующий:

1. Вызов inorder() для левого поддерева.
2. Обход корня.
3. Вызовите inorder() для правого поддерева.

Порядок обхода дерева выше:

Java-код выглядит следующим образом:

 static void inorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse left inorder(TreeNode.left); // Traverse root System.out.print(TreeNode.item + "->"); // Traverse right inorder(TreeNode.right); > 

3. Обход после заказа

Обход двоичного дерева в обратном порядке сначала проходит по левому поддереву, затем по правому поддереву и, наконец, по корню.

Алгоритм обхода после заказа следующий:

1. Вызов postorder() для левого поддерева.
2. Вызов postorder() для правого поддерева.
3. Обход корня.

Пост-порядковый обход дерева выше:

Java-код выглядит следующим образом:

 static void postorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse left postorder(TreeNode.left); // Traverse right postorder(TreeNode.right); // Traverse root System.out.print(TreeNode.item + "->"); > 

4. Обход по уровням

Обход по порядку уровней использует очередь для отслеживания посещаемых узлов. После посещения узла его потомки помещаются в очередь. Чтобы получить новый узел для обхода, мы удаляем элементы из очереди.

1. Инициализировать пустую очередь
2. Начните с установки temp от имени пользователя root
3. Запускать цикл до тех пор, пока очередь не станет пустой
   1. Печатать данные из временного файла.
   2. Поставить дочерние элементы temp в порядке слева и справа.
   3. Удалить узел из очереди и присвоить его значение переменной temp.

   Обход по порядку уровней дерева выше:

   Java-код выглядит следующим образом:

    static void printLevelOrder(TreeNode root) < Queuequeue = new LinkedList(); queue.add(root); while (!queue.isEmpty()) < TreeNode temp = queue.poll(); System.out.print(temp.data + " "); /*add left child to the queue */ if (temp.left != null) < queue.add(temp.left); >/*add right right child to the queue */ if (temp.right != null) < queue.add(temp.right); >> > 

   Полная реализация кода BFS и DFS на Java

   Полный код Java приведен ниже:

   package com.JournalDev; import java.util.LinkedList; import java.util.Queue; public class Main < static class TreeNode < int data; TreeNode left, right; public TreeNode(int key) < data = key; left = right = null; >> static void preorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse root System.out.print(TreeNode.data + " "); // Traverse left preorder(TreeNode.left); // Traverse right preorder(TreeNode.right); >static void inorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse left inorder(TreeNode.left); // Traverse root System.out.print(TreeNode.data + " "); // Traverse right inorder(TreeNode.right); >static void postorder(TreeNode TreeNode) < if (TreeNode == null) return; // Traverse left postorder(TreeNode.left); // Traverse right postorder(TreeNode.right); // Traverse root System.out.print(TreeNode.data + " "); >static void printLevelOrder(TreeNode root) < Queuequeue = new LinkedList(); queue.add(root); while (!queue.isEmpty()) < TreeNode tempNode = queue.poll(); System.out.print(tempNode.data + " "); /*add left child to the queue */ if (tempNode.left != null) < queue.add(tempNode.left); >/*add right right child to the queue */ if (tempNode.right != null) < queue.add(tempNode.right); >> > public static void main(String args[]) < TreeNode root = new TreeNode(0); root.left = new TreeNode(1); root.right = new TreeNode(2); root.left.left = new TreeNode(3); root.left.right = new TreeNode(4); System.out.println("Inorder traversal"); inorder(root); System.out.println("\nPreorder traversal "); preorder(root); System.out.println("\nPostorder traversal"); postorder(root); System.out.println("\nLevelorder traversal"); printLevelOrder(root); >> 

   Output : Inorder traversal 3 1 4 0 2 Preorder traversal 0 1 3 4 2 Postorder traversal 3 4 1 2 0 Levelorder traversal 0 1 2 3 4 

   

   Заключение

   Это руководство было посвящено обходам BFS и DFS в двоичных деревьях. Чтобы получить реализацию DFS на C++, обратитесь к этому руководству.

   Источник

   Реализация бинарного дерева в Java

   В этом руководстве мы рассмотрим реализацию двоичного дерева в Java.

   Для этого руководства мы будем использовать отсортированное двоичное дерево , содержащее значения int .

   2. Бинарное дерево​

   Бинарное дерево — это рекурсивная структура данных, в которой каждый узел может иметь не более двух дочерних элементов.

   Распространенным типом бинарного дерева является бинарное дерево поиска , в котором каждый узел имеет значение, которое больше или равно значениям узлов в левом поддереве и меньше или равно значениям узлов в правом поддереве. дерево.

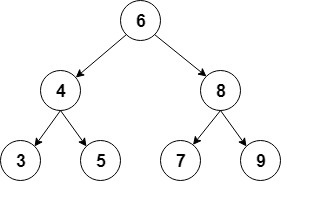
   Вот визуальное представление этого типа бинарного дерева:

   

   Для реализации мы будем использовать вспомогательный класс Node , который будет хранить значения int и сохранять ссылку на каждого дочернего элемента:

    class Node    int value;   Node left;   Node right;    Node(int value)    this.value = value;   right = null;   left = null;   >   > 

   Затем мы добавим начальный узел нашего дерева, обычно называемый корнем:

    public class BinaryTree     Node root;    // .   > 

   3. Общие операции​

   Теперь давайте посмотрим на наиболее распространенные операции, которые мы можем выполнять с бинарным деревом.

   3.1. Вставка элементов​

   Первая операция, которую мы рассмотрим, — это вставка новых узлов.

   Во- первых, мы должны найти место, где мы хотим добавить новый узел, чтобы сохранить сортировку дерева . Мы будем следовать этим правилам, начиная с корневого узла:

   • если значение нового узла ниже, чем значение текущего узла, мы переходим к левому дочернему элементу.
   • если значение нового узла больше, чем значение текущего узла, мы переходим к правому дочернему элементу.
   • когда текущий узел равен нулю, мы достигли конечного узла и можем вставить новый узел в эту позицию.

   Затем мы создадим рекурсивный метод для вставки:

    private Node addRecursive(Node current, int value)    if (current == null)    return new Node(value);   >    if (value  current.value)    current.left = addRecursive(current.left, value);   > else if (value > current.value)    current.right = addRecursive(current.right, value);   > else    // value already exists   return current;   >    return current;   > 

   Далее мы создадим общедоступный метод, который запускает рекурсию с корневого узла:

    public void add(int value)    root = addRecursive(root, value);   > 

   Давайте посмотрим, как мы можем использовать этот метод для создания дерева из нашего примера:

    private BinaryTree createBinaryTree()    BinaryTree bt = new BinaryTree();    bt.add(6);   bt.add(4);   bt.add(8);   bt.add(3);   bt.add(5);   bt.add(7);   bt.add(9);    return bt;   > 

   3.2. Поиск элемента​

   Теперь добавим метод для проверки наличия в дереве определенного значения.

   Как и прежде, мы сначала создадим рекурсивный метод, который проходит по дереву:

    private boolean containsNodeRecursive(Node current, int value)    if (current == null)    return false;   >   if (value == current.value)    return true;   >   return value  current.value  ? containsNodeRecursive(current.left, value)   : containsNodeRecursive(current.right, value);   > 

   Здесь мы ищем значение, сравнивая его со значением в текущем узле; затем мы продолжим в левом или правом дочернем элементе в зависимости от результата.

   Далее мы создадим общедоступный метод, который начинается с корня :

    public boolean containsNode(int value)    return containsNodeRecursive(root, value);   > 

   Затем мы создадим простой тест, чтобы убедиться, что дерево действительно содержит вставленные элементы:

    @Test   public void givenABinaryTree_WhenAddingElements_ThenTreeContainsThoseElements()    BinaryTree bt = createBinaryTree();    assertTrue(bt.containsNode(6));   assertTrue(bt.containsNode(4));    assertFalse(bt.containsNode(1));   > 

   Все добавленные узлы должны содержаться в дереве.

   3.3. Удаление элемента​

   Другой распространенной операцией является удаление узла из дерева.

   Во-первых, мы должны найти удаляемый узел так же, как и раньше:

    private Node deleteRecursive(Node current, int value)    if (current == null)    return null;   >    if (value == current.value)    // Node to delete found   // . code to delete the node will go here   >   if (value  current.value)    current.left = deleteRecursive(current.left, value);   return current;   >   current.right = deleteRecursive(current.right, value);   return current;   > 

   Как только мы находим узел для удаления, есть 3 основных разных случая:

   • узел не имеет потомков — это самый простой случай; нам просто нужно заменить этот узел на null в его родительском узле
   • у узла есть ровно один дочерний элемент — в родительском узле мы заменяем этот узел его единственным дочерним элементом.
   • узел имеет двух детей — это самый сложный случай, потому что он требует реорганизации дерева

   Давайте посмотрим, как бы мы реализовали первый случай, когда узел является листовым узлом:

   Теперь продолжим со случаем, когда у узла есть один дочерний элемент:

    if (current.right == null)    return current.left;   >    if (current.left == null)    return current.right;   > 

   Здесь мы возвращаем ненулевой дочерний элемент, чтобы его можно было назначить родительскому узлу.

   Наконец, нам нужно обработать случай, когда у узла есть два потомка.

   Во-первых, нам нужно найти узел, который заменит удаленный узел. Мы будем использовать наименьший узел правого поддерева узла, который скоро будет удален:

    private int findSmallestValue(Node root)    return root.left == null ? root.value : findSmallestValue(root.left);   > 

   Затем мы присваиваем наименьшее значение удаляемому узлу, после чего удаляем его из правого поддерева:

    int smallestValue = findSmallestValue(current.right);  current.value = smallestValue;  current.right = deleteRecursive(current.right, smallestValue);   return current; 

   Наконец, мы создадим общедоступный метод, который запускает удаление из корня :

    public void delete(int value)    root = deleteRecursive(root, value);   > 

   Теперь давайте проверим, что удаление сработало как положено:

    @Test   public void givenABinaryTree_WhenDeletingElements_ThenTreeDoesNotContainThoseElements()    BinaryTree bt = createBinaryTree();    assertTrue(bt.containsNode(9));   bt.delete(9);   assertFalse(bt.containsNode(9));   > 

   4. Обход дерева​

   В этом разделе мы рассмотрим различные способы обхода дерева, подробно рассмотрев поиск в глубину и в ширину.

   Мы будем использовать то же дерево, что и раньше, и проверим порядок обхода для каждого случая.

   4.1. Поиск в глубину​

   Поиск в глубину — это тип обхода, который максимально углубляется в каждого дочернего элемента, прежде чем исследовать следующего брата или сестру.

   Существует несколько способов выполнения поиска в глубину: по порядку, по предварительному заказу и после заказа.

   Обход по порядку состоит из посещения сначала левого поддерева, затем корневого узла и, наконец, правого поддерева:

    public void traverseInOrder(Node node)    if (node != null)    traverseInOrder(node.left);   System.out.print(" " + node.value);   traverseInOrder(node.right);   >   > 

   Если мы вызовем этот метод, вывод консоли покажет обход по порядку:

   Обход в предварительном порядке сначала посещает корневой узел, затем левое поддерево и, наконец, правое поддерево:

    public void traversePreOrder(Node node)    if (node != null)    System.out.print(" " + node.value);   traversePreOrder(node.left);   traversePreOrder(node.right);   >   > 

   Давайте проверим обход предварительного заказа в выводе консоли:

   Обход в обратном порядке посещает левое поддерево, правое поддерево и корневой узел в конце:

    public void traversePostOrder(Node node)    if (node != null)    traversePostOrder(node.left);   traversePostOrder(node.right);   System.out.print(" " + node.value);   >   > 

   4.2. Поиск в ширину​

   Это еще один распространенный тип обхода, который посещает все узлы уровня перед переходом на следующий уровень .

   Этот вид обхода также называется порядком уровней и посещает все уровни дерева, начиная с корня и слева направо.

   Для реализации мы будем использовать очередь для хранения узлов с каждого уровня по порядку. Мы извлечем каждый узел из списка, распечатаем его значения, а затем добавим его дочерние элементы в очередь:

    public void traverseLevelOrder()    if (root == null)    return;   >    QueueNode> nodes = new LinkedList>();   nodes.add(root);    while (!nodes.isEmpty())     Node node = nodes.remove();    System.out.print(" " + node.value);    if (node.left != null)    nodes.add(node.left);   >    if (node.right != null)    nodes.add(node.right);   >   >   > 

   В этом случае порядок узлов будет следующим:

   5. Вывод​

   В этой статье мы узнали, как реализовать отсортированное двоичное дерево в Java и его наиболее распространенные операции.

   Полный исходный код примеров доступен на GitHub .

   Источник