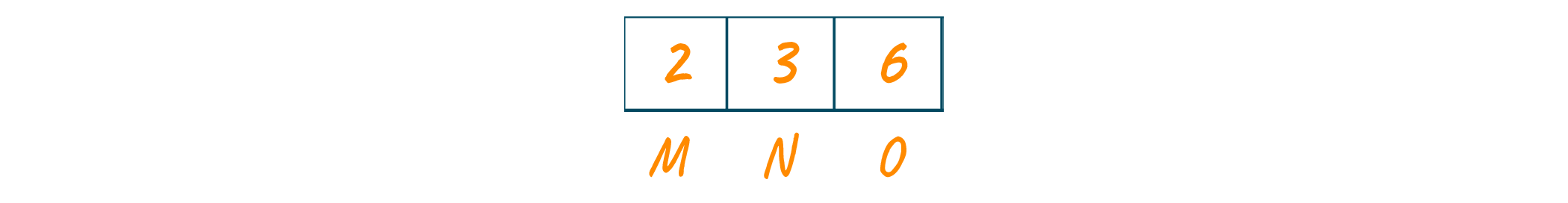Huffman code in python

Huffman Coding with Python

Huffman coding is a lossless way to compress and encode text based on the frequency of the characters in the text. In computer science and information theory, Huffman code is a special type of optimal prefix code that is often used for lossless data compression.

Huffman Coding

The algorithm was developed by David A. Huffman in the late 19th century as part of his research into computer programming and is commonly found in programming languages such as C, C + +, Java, JavaScript, Python, Ruby, and more. The thought process behind Huffman encoding is as follows: a letter or a symbol that occurs frequently is represented by a shorter code, and a letter or symbol that occurs rarely is represented by a longer code. This leads to an efficient representation of characters that require less memory to be stored. This means Huffman coding can be used as a data compression technique.

In this article, we are going to cover the following:

1. The theory of Huffman coding
2. Code snippets to compute the Huffman code for a given string

Theory of Huffman Coding

Huffman coding is based on the frequency with which each character in the file appears and the number of characters in a data structure with a frequency of 0. The Huffman encoding for a typical text file saves about 40% of the size of the original data. We know that a file is stored on a computer as binary code, and that each character in the file has been assigned a binary character, and character codes usually have a fixed length for different characters. Huffman binary code, such as compiled executables, would therefore have a different space-saving. A binary file in which an ASCII character is encoded with a frequency of 0.5 would have a very different distribution and frequency from its ASCII counterpart.

To compress a file with a sequence of characters, we need a table that gives us the sequences of bits used for each character. This table creates an encoding tree that uses the root/leaf path to create a bit sequence that encodes the characters. We can follow the roots and leaves to create a list of all characters with the maximum bit length of the encoded characters and the number of occurrences.

To construct an optimal tree, we use a greedy algorithm. Huffman encoding trees return the minimum length character encodings used in data compression. The nodes in the tree represent the frequency of a character’s occurrence. The root node represents the length of the string, and traversing the tree gives us the character-specific encodings. Once the tree is constructed, traversing the tree gives us the respective codes for each symbol.

The optimal tree upon completion is given in the image below: Image Source

We will develop and implement a program that uses Huffman coding in the next section.

Code

We first define a class called HuffmanCode which is initialized with probabilities. Let us look at the flow of the code implemented below:

1. Obtain the string and compute the frequency of each character in the string
2. Using the frequency, obtain the probabilities
3. Using the algorithm, compute the Huffman codes
4. For the Huffman codes, compute means length, variance, and entropy

Let us look at the algorithm used to compute the Huffman codes.

1. We initially sort the probabilities in decreasing order. This is necessary to assign codes to each symbol according to their frequencies.
2. Run a for loop from 0 to length of string-2
3. For the first symbol assign 1 as the default code
4. For the upcoming symbols, check for the previous symbols
   • If 1- add 0
   • If 11- add 1
   • If 10 — add 0
   • If 111 — add 1
5. Once the Huffman codes are generated, read them in the reverse order to obtain the final_code . This is done to generate code as done by the tree traversal.
6. final_code is the list that contains all the huffman_codes in the order of the probabilities.

Let us now look at the code. There are a couple of functions defined inside the class which will be explained in the section below.

import math import sys global probabilities probabilities = []  class HuffmanCode:  def __init__(self,probability):  self.probability = probability   def position(self, value, index):  for j in range(len(self.probability)):  if(value >= self.probability[j]):  return j  return index-1   def characteristics_huffman_code(self, code):  length_of_code = [len(k) for k in code]   mean_length = sum([a*b for a, b in zip(length_of_code, self.probability)])   print("Average length of the code: %f" % mean_length)  print("Efficiency of the code: %f" % (entropy_of_code/mean_length))   def compute_code(self):  num = len(self.probability)  huffman_code = ['']*num   for i in range(num-2):  val = self.probability[num-i-1] + self.probability[num-i-2]  if(huffman_code[num-i-1] != '' and huffman_code[num-i-2] != ''):  huffman_code[-1] = ['1' + symbol for symbol in huffman_code[-1]]  huffman_code[-2] = ['0' + symbol for symbol in huffman_code[-2]]  elif(huffman_code[num-i-1] != ''):  huffman_code[num-i-2] = '0'  huffman_code[-1] = ['1' + symbol for symbol in huffman_code[-1]]  elif(huffman_code[num-i-2] != ''):  huffman_code[num-i-1] = '1'  huffman_code[-2] = ['0' + symbol for symbol in huffman_code[-2]]  else:  huffman_code[num-i-1] = '1'  huffman_code[num-i-2] = '0'   position = self.position(val, i)  probability = self.probability[0:(len(self.probability) - 2)]  probability.insert(position, val)  if(isinstance(huffman_code[num-i-2], list) and isinstance(huffman_code[num-i-1], list)):  complete_code = huffman_code[num-i-1] + huffman_code[num-i-2]  elif(isinstance(huffman_code[num-i-2], list)):  complete_code = huffman_code[num-i-2] + [huffman_code[num-i-1]]  elif(isinstance(huffman_code[num-i-1], list)):  complete_code = huffman_code[num-i-1] + [huffman_code[num-i-2]]  else:  complete_code = [huffman_code[num-i-2], huffman_code[num-i-1]]   huffman_code = huffman_code[0:(len(huffman_code)-2)]  huffman_code.insert(position, complete_code)   huffman_code[0] = ['0' + symbol for symbol in huffman_code[0]]  huffman_code[1] = ['1' + symbol for symbol in huffman_code[1]]   if(len(huffman_code[1]) == 0):  huffman_code[1] = '1'   count = 0  final_code = ['']*num   for i in range(2):  for j in range(len(huffman_code[i])):  final_code[count] = huffman_code[i][j]  count += 1   final_code = sorted(final_code, key=len)  return final_code  string = input("Enter the string to compute Huffman Code: ")  freq = <> for c in string:  if c in freq:  freq[c] += 1  else:  freq[c] = 1  freq = sorted(freq.items(), key=lambda x: x[1], reverse=True) length = len(string)  probabilities = [float(" ".format(frequency[1]/length)) for frequency in freq] probabilities = sorted(probabilities, reverse=True)  huffmanClassObject = HuffmanCode(probabilities) P = probabilities  huffman_code = huffmanClassObject.compute_code()  print(' Char | Huffman code ') print('----------------------')  for id,char in enumerate(freq):  if huffman_code[id]=='':  print(' %-4r |%12s' % (char[0], 1))  continue  print(' %-4r |%12s' % (char[0], huffman_code[id]))  huffmanClassObject.characteristics_huffman_code(huffman_code) 

Auxiliary Functions

We have a couple of auxiliary functions such as find_position and characteristics_huffman_code . find_position is used to insert bits to the existing code computed in the n-3 previous iterations, where n is the length.

The second auxiliary function defined is characteristics_huffman_code . This function generates the mean length of the codes, entropy, variance, and efficiency. Let us look at each of these in detail

Performance of Huffman Code

1. Average Length: It is defined as the average number of bits required to represent a character in the string.
2. Efficiency: Efficiency is a measure of the number of bits wasted. An efficiency of 0.945 means for every 100 bits 5.5 bits are wasted. This deals with the concept of entropy. Entropy is a quantitative measure for the amount of information a code provides. Any repetition results in redundancy thereby reducing the information per unit symbol. Thus decreasing efficiency.

Conclusion

In this article, we have discussed what Huffman coding is, some of its applications, and have also considered a code snippet that encodes a given text based on the frequency of characters. I hope you have enjoyed the article. I suggest you implement the code and use this guide as you code-along.

Peer Review Contributions by: Nadiv Gold Edelstein

Источник

Huffman Coding with Python Implementation (full code)

Huffman coding is a type of greedy algorithm developed by David A. Huffman during the late 19 th century. It is one of the most used algorithms for various purposes all over the technical domain. In this article, we will study Huffman coding, example, algorithm, and its implementation using python.

What is Huffman Coding?

Huffman coding is a greedy algorithm frequently used for lossless data compression. The basic principle of Huffman coding is to compress and encode the text or the data depending on the frequency of the characters in the text.

The idea of this algorithm is to assign variable-length codes to input characters of text based on the frequencies of the corresponding character. So, the most frequent character gets the smallest code, and the least frequent character is assigned the largest code.

Here, the codes assigned to the characters are termed prefix codes which means that the code assigned to one character is not the prefix of the code assigned to any other character. Using this technique, Huffman coding ensures that there is no ambiguity when decoding the generated bitstream.

Is Huffman coding a Greedy algorithm?

Yes, Huffman coding is a greedy algorithm. It works by selecting the lowest two frequency symbols/subtrees and merging them together at every step until all symbols or subtrees are merged into a single binary tree. This method ensures that the final binary tree minimizes the total number of bits required to represent the symbols in the input.

As a result, Huffman coding is regarded as a classic example of a greedy algorithm.

Huffman Coding Example

Let us understand how Huffman coding works with the example below:

Consider the following input text:

As the above text is of 11 characters, each character requires 8 bits. Therefore, a total of 11×8=88 bits are required to send this input text.

Using Huffman coding, we will compress the text to a smaller size by creating a Huffman coding tree using the character frequencies and generating the code for each character.

Remember that we encode the text while sending it, and later, it is necessary to decode it. Hence, the decoding of the text is done using the same tree generated by the Huffman technique.

Let us see how to encode the above text using the Huffman coding algorithm:

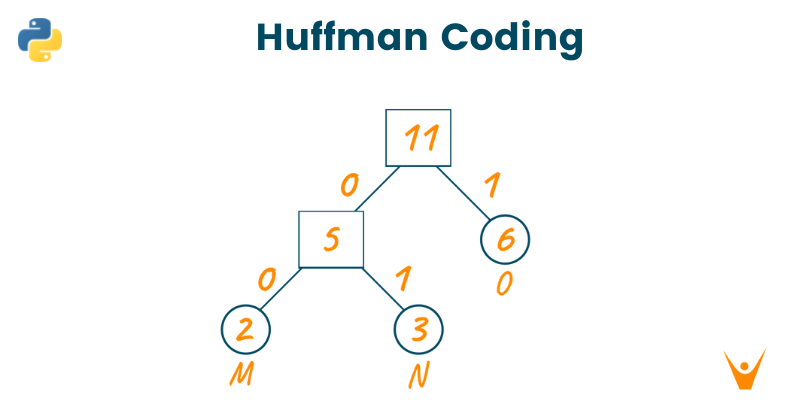
Looking at the text, the frequencies of the characters will be as shown in the below image.

Now, we will sort the frequencies string of the characters in increasing order. Consider these characters are stored in the priority queue as shown in the below image.

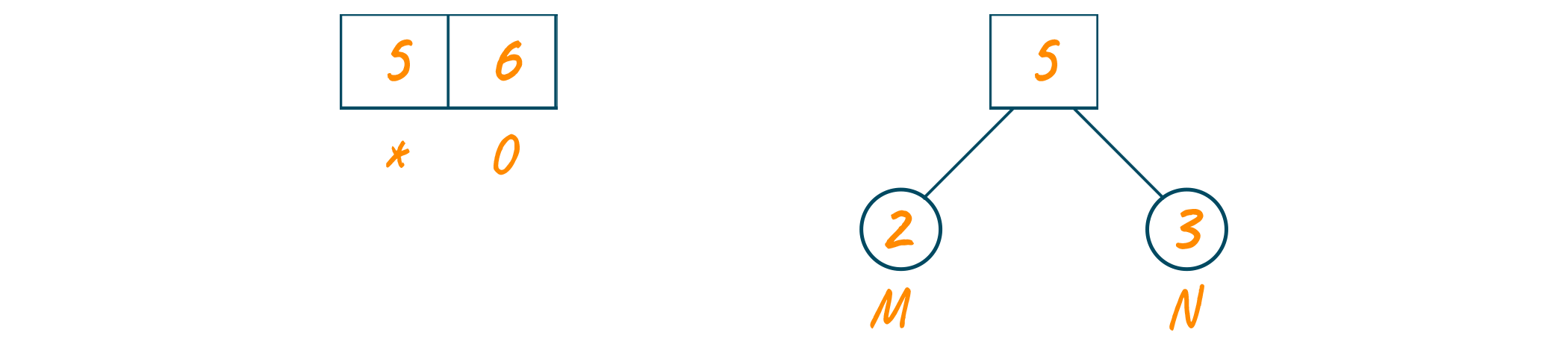
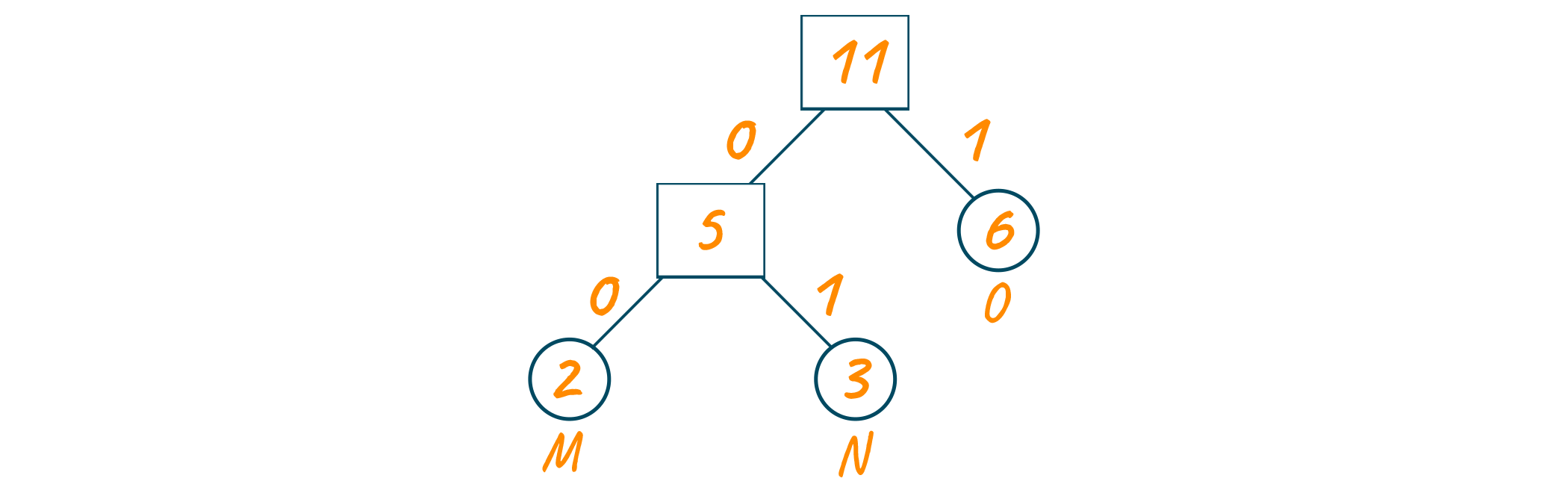
Now, we will create the Huffman tree using this priority queue. Here, we will create an empty node ‘a’. Later, we will assign the minimum frequency of the queue as the left child of node ‘a’ and the second minimum frequency as the right child of node ‘a’.

The value of node ‘a’ will be the sum of both minimum frequencies and add it to the priority queue as shown in the below image.

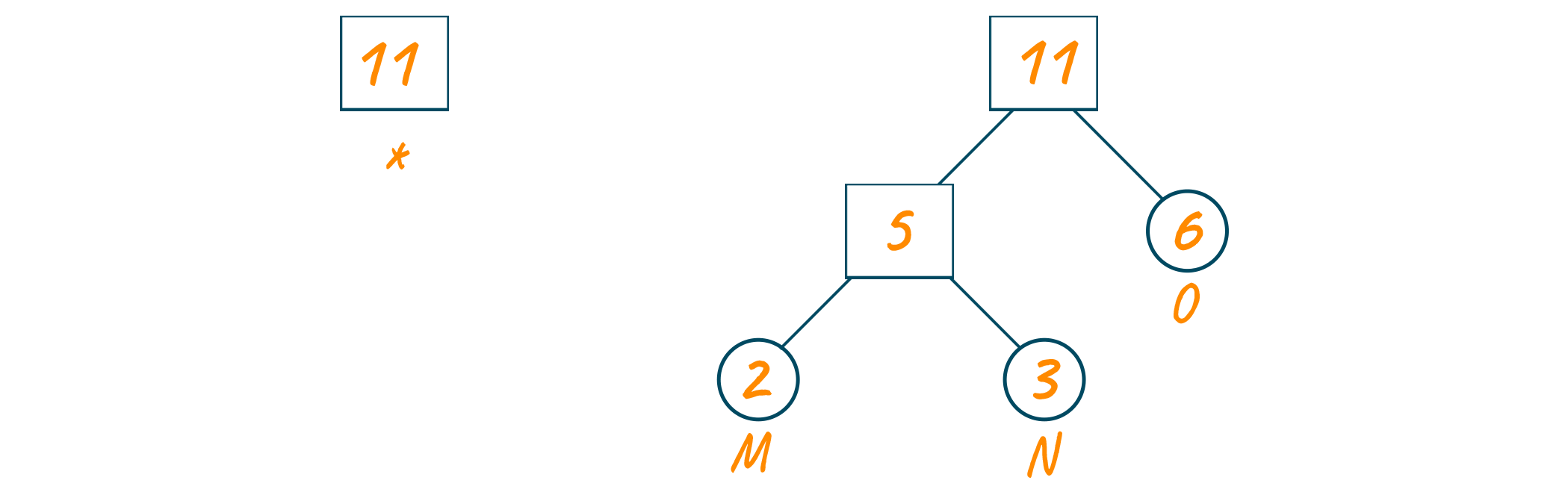
Repeat the same process until the complete Huffman tree is formed.

Now, assign 0 to the left edges and 1 to the right edges of the Huffman coding tree as shown below.

Remember that for sending the above text, we will send the tree along with the compressed code for easy decoding. Therefore, the total size is given in the table below:

Источник