numpy.histogram2d#
Compute the bi-dimensional histogram of two data samples.
Parameters : x array_like, shape (N,)
An array containing the x coordinates of the points to be histogrammed.
y array_like, shape (N,)
An array containing the y coordinates of the points to be histogrammed.
bins int or array_like or [int, int] or [array, array], optional
- If int, the number of bins for the two dimensions (nx=ny=bins).
- If array_like, the bin edges for the two dimensions (x_edges=y_edges=bins).
- If [int, int], the number of bins in each dimension (nx, ny = bins).
- If [array, array], the bin edges in each dimension (x_edges, y_edges = bins).
- A combination [int, array] or [array, int], where int is the number of bins and array is the bin edges.
The leftmost and rightmost edges of the bins along each dimension (if not specified explicitly in the bins parameters): [[xmin, xmax], [ymin, ymax]] . All values outside of this range will be considered outliers and not tallied in the histogram.
density bool, optional
If False, the default, returns the number of samples in each bin. If True, returns the probability density function at the bin, bin_count / sample_count / bin_area .
weights array_like, shape(N,), optional
An array of values w_i weighing each sample (x_i, y_i) . Weights are normalized to 1 if density is True. If density is False, the values of the returned histogram are equal to the sum of the weights belonging to the samples falling into each bin.
Returns : H ndarray, shape(nx, ny)
The bi-dimensional histogram of samples x and y. Values in x are histogrammed along the first dimension and values in y are histogrammed along the second dimension.
xedges ndarray, shape(nx+1,)
The bin edges along the first dimension.
yedges ndarray, shape(ny+1,)
The bin edges along the second dimension.
When density is True, then the returned histogram is the sample density, defined such that the sum over bins of the product bin_value * bin_area is 1.
Please note that the histogram does not follow the Cartesian convention where x values are on the abscissa and y values on the ordinate axis. Rather, x is histogrammed along the first dimension of the array (vertical), and y along the second dimension of the array (horizontal). This ensures compatibility with histogramdd .
>>> from matplotlib.image import NonUniformImage >>> import matplotlib.pyplot as plt
Construct a 2-D histogram with variable bin width. First define the bin edges:
>>> xedges = [0, 1, 3, 5] >>> yedges = [0, 2, 3, 4, 6]
Next we create a histogram H with random bin content:
>>> x = np.random.normal(2, 1, 100) >>> y = np.random.normal(1, 1, 100) >>> H, xedges, yedges = np.histogram2d(x, y, bins=(xedges, yedges)) >>> # Histogram does not follow Cartesian convention (see Notes), >>> # therefore transpose H for visualization purposes. >>> H = H.T
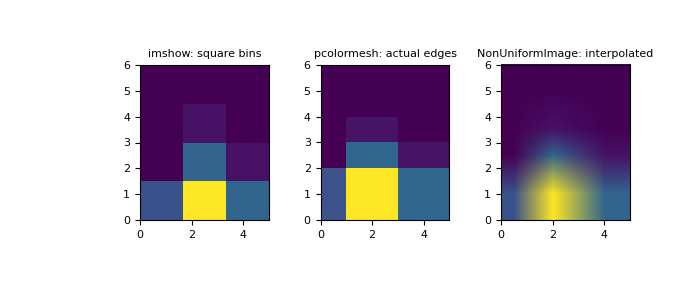
imshow can only display square bins:
>>> fig = plt.figure(figsize=(7, 3)) >>> ax = fig.add_subplot(131, title=‘imshow: square bins’) >>> plt.imshow(H, interpolation=‘nearest’, origin=‘lower’, . extent=[xedges[0], xedges[—1], yedges[0], yedges[—1]])
>>> ax = fig.add_subplot(132, title=‘pcolormesh: actual edges’, . aspect=‘equal’) >>> X, Y = np.meshgrid(xedges, yedges) >>> ax.pcolormesh(X, Y, H)
NonUniformImage can be used to display actual bin edges with interpolation:
>>> ax = fig.add_subplot(133, title='NonUniformImage: interpolated', . aspect='equal', xlim=xedges[[0, -1]], ylim=yedges[[0, -1]]) >>> im = NonUniformImage(ax, interpolation='bilinear') >>> xcenters = (xedges[:-1] + xedges[1:]) / 2 >>> ycenters = (yedges[:-1] + yedges[1:]) / 2 >>> im.set_data(xcenters, ycenters, H) >>> ax.add_image(im) >>> plt.show()
It is also possible to construct a 2-D histogram without specifying bin edges:
>>> # Generate non-symmetric test data >>> n = 10000 >>> x = np.linspace(1, 100, n) >>> y = 2*np.log(x) + np.random.rand(n) - 0.5 >>> # Compute 2d histogram. Note the order of x/y and xedges/yedges >>> H, yedges, xedges = np.histogram2d(y, x, bins=20)
Now we can plot the histogram using pcolormesh , and a hexbin for comparison.
>>> # Plot histogram using pcolormesh >>> fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True) >>> ax1.pcolormesh(xedges, yedges, H, cmap='rainbow') >>> ax1.plot(x, 2*np.log(x), 'k-') >>> ax1.set_xlim(x.min(), x.max()) >>> ax1.set_ylim(y.min(), y.max()) >>> ax1.set_xlabel('x') >>> ax1.set_ylabel('y') >>> ax1.set_title('histogram2d') >>> ax1.grid()
>>> # Create hexbin plot for comparison >>> ax2.hexbin(x, y, gridsize=20, cmap='rainbow') >>> ax2.plot(x, 2*np.log(x), 'k-') >>> ax2.set_title('hexbin') >>> ax2.set_xlim(x.min(), x.max()) >>> ax2.set_xlabel('x') >>> ax2.grid()
numpy.histogram#
Input data. The histogram is computed over the flattened array.
bins int or sequence of scalars or str, optional
If bins is an int, it defines the number of equal-width bins in the given range (10, by default). If bins is a sequence, it defines a monotonically increasing array of bin edges, including the rightmost edge, allowing for non-uniform bin widths.
If bins is a string, it defines the method used to calculate the optimal bin width, as defined by histogram_bin_edges .
range (float, float), optional
The lower and upper range of the bins. If not provided, range is simply (a.min(), a.max()) . Values outside the range are ignored. The first element of the range must be less than or equal to the second. range affects the automatic bin computation as well. While bin width is computed to be optimal based on the actual data within range, the bin count will fill the entire range including portions containing no data.
weights array_like, optional
An array of weights, of the same shape as a. Each value in a only contributes its associated weight towards the bin count (instead of 1). If density is True, the weights are normalized, so that the integral of the density over the range remains 1.
density bool, optional
If False , the result will contain the number of samples in each bin. If True , the result is the value of the probability density function at the bin, normalized such that the integral over the range is 1. Note that the sum of the histogram values will not be equal to 1 unless bins of unity width are chosen; it is not a probability mass function.
Returns : hist array
The values of the histogram. See density and weights for a description of the possible semantics.
bin_edges array of dtype float
Return the bin edges (length(hist)+1) .
All but the last (righthand-most) bin is half-open. In other words, if bins is:
then the first bin is [1, 2) (including 1, but excluding 2) and the second [2, 3) . The last bin, however, is [3, 4] , which includes 4.
>>> np.histogram([1, 2, 1], bins=[0, 1, 2, 3]) (array([0, 2, 1]), array([0, 1, 2, 3])) >>> np.histogram(np.arange(4), bins=np.arange(5), density=True) (array([0.25, 0.25, 0.25, 0.25]), array([0, 1, 2, 3, 4])) >>> np.histogram([[1, 2, 1], [1, 0, 1]], bins=[0,1,2,3]) (array([1, 4, 1]), array([0, 1, 2, 3]))
>>> a = np.arange(5) >>> hist, bin_edges = np.histogram(a, density=True) >>> hist array([0.5, 0. , 0.5, 0. , 0. , 0.5, 0. , 0.5, 0. , 0.5]) >>> hist.sum() 2.4999999999999996 >>> np.sum(hist * np.diff(bin_edges)) 1.0
Automated Bin Selection Methods example, using 2 peak random data with 2000 points:
>>> import matplotlib.pyplot as plt >>> rng = np.random.RandomState(10) # deterministic random data >>> a = np.hstack((rng.normal(size=1000), . rng.normal(loc=5, scale=2, size=1000))) >>> _ = plt.hist(a, bins='auto') # arguments are passed to np.histogram >>> plt.title("Histogram with 'auto' bins") Text(0.5, 1.0, "Histogram with 'auto' bins") >>> plt.show()
Метод numpy.histogram() в Python — гистограмма массива
Метод numpy.histogram() в Python вычисляет «гистограмму массива». Гистограмма — это графическое представление распределения данных. Это столбчатая диаграмма, где ось x представляет ячейки данных(интервалы), а ось y представляет количество точек данных в каждой ячейке.
Синтаксис
numpy . histogram ( arr , bins = 10 , range = None , normed = None , weights = None , density = None )
Аргументы
Функция np.histogram() принимает один обязательный аргумент в качестве параметра и имеет пять необязательных аргументов:
- arr: в этом аргументе передается массив. Массив является обязательным аргументом для возврата гистограммы.
- bins: это количество бинов. Десять хранятся в качестве бинов по умолчанию. Значение этого аргумента может быть последовательностью чисел, int или str. Если это int, то ширина бинов создается одинаково. Если это список, то значения ячеек меняются.
- range: это диапазон, в котором значения будут рассматриваться. Если значение превышает диапазон, то это значение не будет учитываться. Диапазон состоит из двух значений, начального и конечного, заключен в кортеж. Этот кортеж состоит из( start, end ) начального и конечного значений в диапазоне.
- normed: похож на аргумент density.
- weight: этот аргумент передается с массивом, состоящим из весов. Форма этого массива должна быть равна форме массива a. Аргумент weight нормализуется, если для параметра density задано значение True.
- density: если это True, то значение функции плотности вероятно. Если False, массив будет иметь количество выборок в каждой ячейке.
Возвращаемое значение numpy.histogram()
Метод возвращает два значения. Одно представляет собой массив значений гистограммы, а другое состоит из границ бинов.