Graph python как работать

Как работать с графами и деревьями в Python

Изучите создание и работу с графами и деревьями в Python с помощью практических примеров и полезных библиотек.

Графы и деревья являются важными структурами данных в программировании, особенно в области алгоритмов и обработки данных. В этой статье мы рассмотрим, как работать с графами и деревьями в Python, используя различные библиотеки и подходы.

Основы графов и деревьев

Графы — это структуры данных, состоящие из вершин (узлов) и ребер, которые соединяют эти вершины. Деревья являются частным случаем графов, в которых нет циклов, и есть корень, от которого идут пути ко всем остальным вершинам.

Работа с графами

Для работы с графами в Python мы можем использовать библиотеку NetworkX. Давайте установим ее с помощью следующей команды:

Теперь давайте создадим простой граф и добавим в него несколько вершин и ребер.

import networkx as nx G = nx.Graph() G.add_node(1) G.add_nodes_from([2, 3, 4]) G.add_edge(1, 2) G.add_edges_from([(1, 3), (2, 4), (3, 4)]) print(G.nodes) print(G.edges)

Работа с деревьями

Для работы с деревьями в Python можно использовать библиотеку treelib . Установим ее с помощью команды:

Теперь создадим простое дерево и добавим в него несколько узлов.

import treelib tree = treelib.Tree() tree.create_node("Root", 1) tree.create_node("Child1", 2, parent=1) tree.create_node("Child2", 3, parent=1) tree.create_node("Grandchild1", 4, parent=2) tree.create_node("Grandchild2", 5, parent=2) tree.show()

😉 Вот так просто можно создавать и работать с графами и деревьями в Python. Попробуйте сами и не забывайте изучать документацию к библиотекам для более глубокого погружения в возможности работы с графами и деревьями.

Источник

python graph

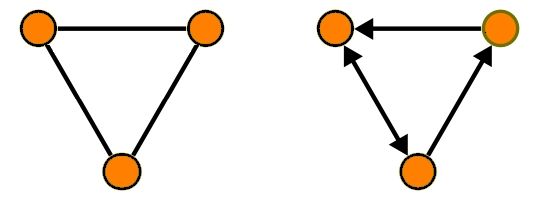
A graph in mathematics and computer science consists of “nodes” which may or may not be connected with one another. Connections between nodes are called edges. A graph can be directed (arrows) or undirected. The edges could represent distance or weight.

default graph (left), directed graph (right)

Python does not have a graph data type. To use graphs we can either use a module or implement it ourselves:

Graph in Python

#!/usr/bin/env python

graph = {‘A’: [‘B’, ‘C’],
‘B’: [‘C’, ‘A’],
‘C’: [‘D’],
‘D’: [‘A’]}

print(graph)

Graphs using networkx

#!/usr/bin/env python
import networkx as nx

G=nx.Graph()
G.add_node(«A»)
G.add_node(«B»)
G.add_node(«C»)
G.add_edge(«A»,«B»)
G.add_edge(«B»,«C»)
G.add_edge(«C»,«A»)

print(«Nodes: « + str(G.nodes()))
print(«Edges: « + str(G.edges()))
Nodes: [‘A’, ‘C’, ‘B’]Edges: [(‘A’, ‘C’), (‘A’, ‘B’), (‘C’, ‘B’)]

Источник

работа с графами в Python

Будет использоваться ненаправленный связный граф V=6 E=6. Существует две популярные методики представления графов: матрица смежности (эффективна с плотными графами) и список связей (эффективно с разряженными графами). Будем использовать второй способ.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']>

2 Depth-First Search — Поиск вглубину

Алгоритм поиска вглубину: исследуем сначала все возможные вершины (из выбранного корня) доступные из текущей, прежде чем возвращаться назад. Данный алгоритм можно реализовать как рекурсивно, так и итеративно. Последовательность действий:

• Помечаем текущую вершину как посещённую
• Исследуем каждую соседнюю вершину не включённую в список уже посещённых
• Вариант с DFS and BFS in Python (модифицированный, т.к. set не поддерживает упорядоченность элементов)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs(graph, start): visited, stack = [], [start] while stack: vertex = stack.pop() if vertex not in visited: visited.append(vertex) stack.extend(set(graph[vertex]) - set(visited)) return visited print(dfs(graph, 'A'))

• Вариант с DFS and BFS graph traversal (Python recipe) (модифицированный, т.к. для реализации стека нам необходимо добавлять элементы в конец списка, а не в начало)

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def iteractive_dfs(graph, start, path=None): """iterative depth first search from start""" if path is None: path = [] q = [start] while q: v = q.pop() if v not in path: path = path + [v] q += graph[v] return path print(iteractive_dfs(graph, 'A'))

3 DFS Paths — поиск пути между двумя вершинами

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def dfs_paths(graph, start, goal): stack = [(start, [start])] # (vertex, path) while stack: (vertex, path) = stack.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: stack.append((next, path + [next])) print(list(dfs_paths(graph, 'A', 'F')))

4 Bread-Firsth Search — Поиск вширину

Позволяет найти кратчайший путь между двумя вершинами. Довольно сложно реализовать рекурсивно, гораздо проще реализовать его с использованием очереди.

graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> from queue import deque def bfs(graph, start): visited, queue = [], deque([start]) while queue: vertex = queue.pop() if vertex not in visited: visited.append(vertex) queue.extendleft(set(graph[vertex]) - set(visited)) return visited print(bfs(graph, 'A'))

5 BFS Paths

from queue import deque graph = 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']> def bfs_paths(graph, start, goal): queue = deque([(start, [start])]) while queue: (vertex, path) = queue.pop() for next in set(graph[vertex]) - set(path): if next == goal: yield path + [next] else: queue.appendleft((next, path+[next])) print(list(bfs_paths(graph, 'A', 'F'))) def shortest_path(graph, start, goal): try: return next(bfs_paths(graph, start, goal)) except StopIteration: return None print(shortest_path(graph, 'A', 'F')) print(shortest_path(graph, 'E', 'D')) print(shortest_path(graph, 'A', 'D')) print(shortest_path(graph, 'F', 'D'))

[['A', 'C', 'F'], ['A', 'B', 'E', 'F']] ['A', 'C', 'F'] ['E', 'B', 'D'] ['A', 'B', 'D'] ['F', 'E', 'B', 'D']

Created: 2017-11-09 Thu 19:40

Источник