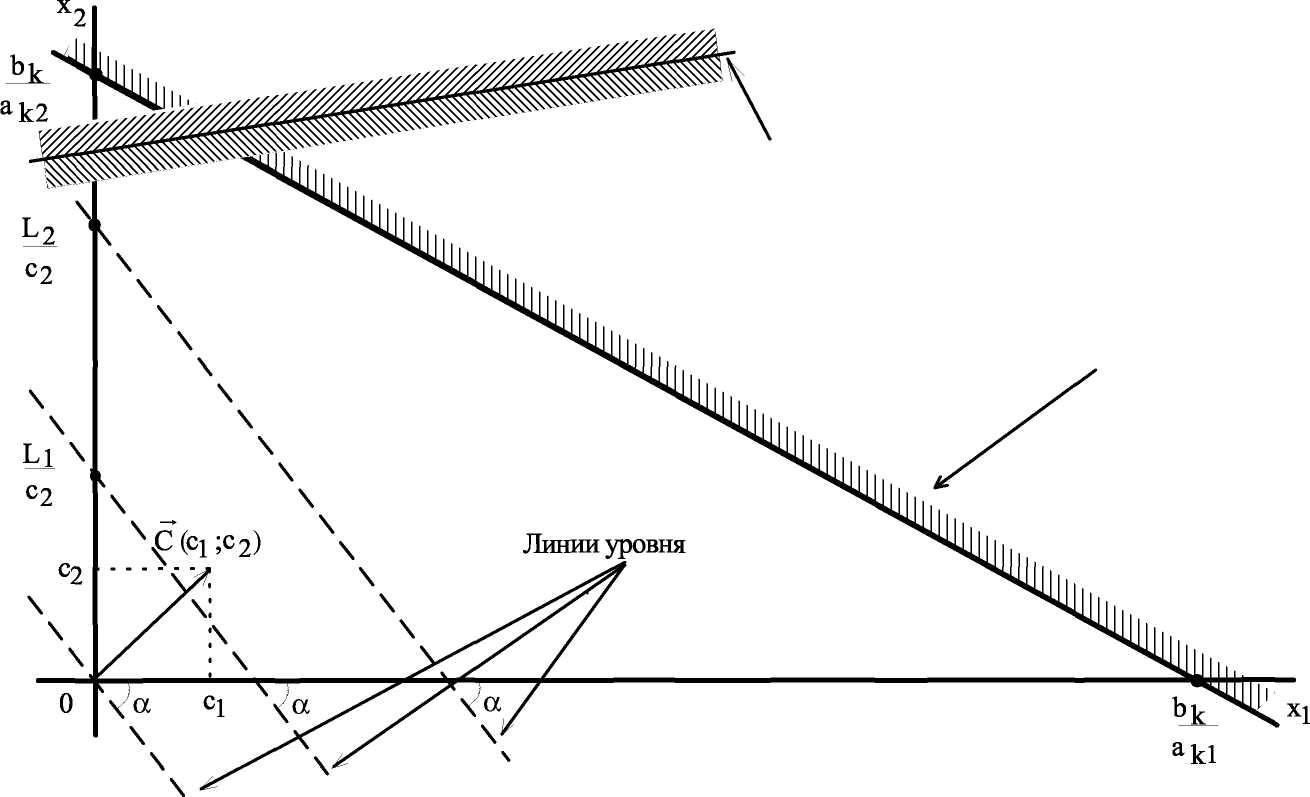
Графический метод решения задач линейного программирования вывод

Графический метод решения задачи линейного программирования.

В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).

1. На плоскости X₁0X₂ строят прямые.
2. Определяются полуплоскости.
3. Определяют многоугольник решений;
4. Строят вектор N(c₁,c₂), который указывает направление целевой функции;
5. Передвигают прямую целевую функцию c₁x₂+ c₂x₂ = 0 в направлении вектора N до крайней точки многоугольника решений.

Вычисляют координаты точки и значение целевой функции в этой точке.

Алгоритмический метод.

Для усвоения симплексного метода, а также других алгоритмов, рассмотренных в последующих главах, полезно иметь представление о некоторых основных моментах, учитываемых при использовании любой вычислительной процедуры. Оценивая тот или иной вычислительный алгоритм, необходимо, в частности, рассмотреть следующие его характеристики:

Рассмотренные выше методы служат для сбора информации о субъекте труда или профессиональной среде. Вместе с тем существует ряд методов упорядочения полученной информации. Одним из таких методов является алгоритмический анализ. Алгоритм — строгая последовательность действий, которая неизбежно приводит к решению задачи определенного класса. Эта последовательность действий может иметь словесное описание, в котором представлены все элементарные действия и логические условия, определяющие порядок этих действий, а может быть описана в символической форме или в виде графика. Метод дает возможность представить совокупность действий в компактной форме и понять их закономерные связи. Благодаря своей полноценности, конкретности и систематичности алгоритмы позволяют постепенно проследить характер операций, выполняемых работниками, и установить те звенья процесса, в которых наиболее часты аварии и брак и которые необходимо рационализировать или автоматизировать в первую очередь, либо функции, требующие перераспределения или изменения.

Существуют также возможности применения алгоритмического подхода при изучении и распространении передового опыта, в процессе обучения рабочих и повышения их квалификации на производстве, для оценки рациональности размещения оборудования, для повышения качества нормирования труда и т. д.

Введение в симплексный алгоритм.

Для решения задач линейного программирования предложено немало различных алгоритмов. Однако наиболее эффективным среди них оказался алгоритм, рассмотренный ниже. При этом следует подчеркнуть, что при решении некоторых частных задач (как, например, задач, связанных с оптимизацией потоков в сетях) могут оказаться более эффективными другие алгоритмы.

Попытаемся ход рассуждений, который был в каком-то разделе учебника выше, описать словесно. Упомянутая модель содержит два уравнения. Пробные решения выбирались следующим образом: допускалось, что две переменные прини­мают некоторые положительные значения, а остальные переменные предполагались тождественно равными нулю. Стремясь к обобщению, можно предположить, что в тех случаях, когда модель содержит т уравнений, для построения пробных решений используются т пере­менных, принимающих некоторые положительные значения при нулевых значениях остальных переменных. Вначале допустим, что решение существует, причем оптимальное значение целевой функции конечно ). В этом случае вычислительная процедура будет выгля­деть следующим образом:

Шаг 1. Выберем т переменных, задающих допустимое пробное решение. Исключим эти переменные из выражения для целевой функции.

Шаг 2. Проверим, нельзя ли за счет одной из переменных, при­равненной вначале к нулю, улучшить значение целевой функции, придавая ей отличные от нуля (причем положительные) значения. Если это возможно, перейдем к шагу 3. В противном случае прекра­тим вычисления.

Шаг 3. Найдем предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из т переменных, вошедших в пробное решение, не обратится в нуль. Исключим из вы­ражения для целевой функции только что упомянутую переменную и введем в пробное решение ту переменную, за счет которой результат может быть улучшен.

Шаг 4. Разрешим систему т уравнений относительно переменных, вошедших в новое пробное решение. Исключим эти переменные из выражения для целевой функции. Вернемся к шагу 2.

Важно отметить, что при однозначном понимании данного пред­писания предложенный алгоритм действительно приводит к опти­мальному решению для любой модели линейного программирования за конечное число итераций. Такой способ решения задач линей­ного программирования часто называют симплексным алгорит­мом.

Обратимся вначале к одной простой задаче, не имеющей никаких «аномалий», и попытаемся с ее помощью получить общее представ­ление о симплексном методе. К более подробному анализу данного метода вернемся несколько позже.

Источник

1.Графический метод решения задач линейного программирования

Графический метод довольно прост и нагляден для решения задач ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.

Каждое из неравенств задачи ЛП определяет на координатной плоскости (х₁,х₂) некоторую полуплоскость (рис. 1), а система неравенств в целом — пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена, выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучом, одной точкой. В случае несовместности системы ограничений задачи ОДР является пустым множеством.

Примечание № 1. Все вышесказанное относится и к случаю, когда система ограничений (1.1) включает равенства, поскольку любое равенство

можно представить в виде системы двух неравенств (рис. 1)

ЦФ L(x)= с1х1 + с2х2 при фиксированном значении L(х)=L определяет на плоскости прямую линию с1х1 + с2х2 = L. Изменяя значения L, мы получим семейство параллельных прямых, называемых линиями уровня.

Это связано с тем, что изменение значения L повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси х2 (начальная ордината), а угловой коэффициент прямой tgа = —- останется постоянным (рис. 1).

Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение L.

Вектор C = (c1;c2) с координатами из коэффициентов ЦФ при х1 и х2 перпендикулярен к каждой из линий уровня (см. рис. 1). Направление вектора С совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора С .

Суть графического метода заключается в следующем. По направлению (против направления) вектора С в ОДР производится поиск оптимальной точки X = (х1; х2). Оптимальной считается точка, через которую проходит линия уровня L_max (L_min), соответствующая наибольшему (наименьшему) значению функции L(x). Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений — единственная точка; задача не имеет решений.

Допустимая область — полуплоскость

1.2. Методика решения задач лп графическим методом

I. В ограничениях задачи замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.

II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи. Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.

Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку; иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.

Поскольку х1 и х2 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси х₁ и правее оси х2, т.е. в 1-м квадранте.

Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.

1. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача неимеет решений,о чем сделайте соответствующий вывод.
2. Если ОДР — не пустое множество, то постройте целевую прямую, т.е. любую из линий уровня с₁х₁ + с₂х₂ = L, где L — произвольное число, например, кратное с₁ и с₂, т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.

V. Постройте вектор C = (c₁,с₂), который начинается в точке (0;0), заканчивается в точке (c₁,с₂). Если целевая прямая и вектор С построены верно, то они будут перпендикулярны. VI. При поиске max ЦФ передвигайте целевую прямую в направлениивектора С, при поиске min ЦФ — против направлениявектора С. Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ намножестве плановсверху (при поиске шах) или снизу (при поиске min). Определите координаты точки max (min) ЦФ X = (х1 * ; х2 * ) и вычислите значение ЦФ l(x * ). Для вычисления координат оптимальной точки X * решите систему уравнений прямых, на пересечении которых находится X * . Задача 1 Найдем оптимальное решение задачи, математическая модель которой имеет вид L(Х) = 3x₁ + 2x₂ → max х₁+ 2х₂< 6, (1) 2х₁+ х₂< 8, (2) -х₁+х₂2< 2, (4) х₁>0,х₂>0. Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис. 2 ). х₁+ 2х₂ = 6,(1) 2х1 +х2= 8,(2) -х1+х2= 1,(3) х2= 2. (4) (1) х1=0, х1=6, х2=3, х2=0, (2) х1=0, х1=4, х2=8, х2=0, (3) х1=0, х1=-1, х2=1, х2=0, Прямая (4) проходит через точку х₂ = 2 параллельно оси L(Х). Рис. 2. Графическое решение задачи Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим 0 < 1, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (рис. 2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDEF. Целевую прямую можно построить по уравнению 3х1 +2×2 = 6, Х1=0, х1=2, Х2=3, х2=0, Строим вектор С из точки (0;0) в точку (3;2). Точка Е- это последняя вершина многоугольника допустимых решений ABCDEF, через которую проходит целевая прямая, двигаясь по направлениювектора С. Поэтому Е -это точка максимума ЦФ. Определим координаты точки Е из системы уравнений прямых ограничений (1) и (2) _Х1+2х₂=6, (1) х1=10/3=3 1/3, х2=4/3=1 1/3 2_Х1+х₂=8, (2) Е 3 1/3; 1 1/3 Максимальное значение ЦФ равно L(E) = 3*10/3+2*4/3 = 12 2 / 3

Источник