Графический метод решения задачи линейного программирования.
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).
- На плоскости X10X2 строят прямые.
- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2+ c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
Вычисляют координаты точки и значение целевой функции в этой точке.
Алгоритмический метод.
Для усвоения симплексного метода, а также других алгоритмов, рассмотренных в последующих главах, полезно иметь представление о некоторых основных моментах, учитываемых при использовании любой вычислительной процедуры. Оценивая тот или иной вычислительный алгоритм, необходимо, в частности, рассмотреть следующие его характеристики:
Рассмотренные выше методы служат для сбора информации о субъекте труда или профессиональной среде. Вместе с тем существует ряд методов упорядочения полученной информации. Одним из таких методов является алгоритмический анализ. Алгоритм — строгая последовательность действий, которая неизбежно приводит к решению задачи определенного класса. Эта последовательность действий может иметь словесное описание, в котором представлены все элементарные действия и логические условия, определяющие порядок этих действий, а может быть описана в символической форме или в виде графика. Метод дает возможность представить совокупность действий в компактной форме и понять их закономерные связи. Благодаря своей полноценности, конкретности и систематичности алгоритмы позволяют постепенно проследить характер операций, выполняемых работниками, и установить те звенья процесса, в которых наиболее часты аварии и брак и которые необходимо рационализировать или автоматизировать в первую очередь, либо функции, требующие перераспределения или изменения.
Существуют также возможности применения алгоритмического подхода при изучении и распространении передового опыта, в процессе обучения рабочих и повышения их квалификации на производстве, для оценки рациональности размещения оборудования, для повышения качества нормирования труда и т. д.
Введение в симплексный алгоритм.
Для решения задач линейного программирования предложено немало различных алгоритмов. Однако наиболее эффективным среди них оказался алгоритм, рассмотренный ниже. При этом следует подчеркнуть, что при решении некоторых частных задач (как, например, задач, связанных с оптимизацией потоков в сетях) могут оказаться более эффективными другие алгоритмы.
Попытаемся ход рассуждений, который был в каком-то разделе учебника выше, описать словесно. Упомянутая модель содержит два уравнения. Пробные решения выбирались следующим образом: допускалось, что две переменные принимают некоторые положительные значения, а остальные переменные предполагались тождественно равными нулю. Стремясь к обобщению, можно предположить, что в тех случаях, когда модель содержит т уравнений, для построения пробных решений используются т переменных, принимающих некоторые положительные значения при нулевых значениях остальных переменных. Вначале допустим, что решение существует, причем оптимальное значение целевой функции конечно ). В этом случае вычислительная процедура будет выглядеть следующим образом:
Шаг 1. Выберем т переменных, задающих допустимое пробное решение. Исключим эти переменные из выражения для целевой функции.
Шаг 2. Проверим, нельзя ли за счет одной из переменных, приравненной вначале к нулю, улучшить значение целевой функции, придавая ей отличные от нуля (причем положительные) значения. Если это возможно, перейдем к шагу 3. В противном случае прекратим вычисления.
Шаг 3. Найдем предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из т переменных, вошедших в пробное решение, не обратится в нуль. Исключим из выражения для целевой функции только что упомянутую переменную и введем в пробное решение ту переменную, за счет которой результат может быть улучшен.
Шаг 4. Разрешим систему т уравнений относительно переменных, вошедших в новое пробное решение. Исключим эти переменные из выражения для целевой функции. Вернемся к шагу 2.
Важно отметить, что при однозначном понимании данного предписания предложенный алгоритм действительно приводит к оптимальному решению для любой модели линейного программирования за конечное число итераций. Такой способ решения задач линейного программирования часто называют симплексным алгоритмом.
Обратимся вначале к одной простой задаче, не имеющей никаких «аномалий», и попытаемся с ее помощью получить общее представление о симплексном методе. К более подробному анализу данного метода вернемся несколько позже.
Графический метод решения задач линейного программирования
Графический метод используется для решения задач с двумя переменными вида: 



- Построить множество допустимых решений. В общем случае оно представляет собой выпуклый многоугольник. Если ограничения в задаче несовместны, множество допустимых решений является пустым множеством, а задача поиска экстремума не имеет смысла.
- Найти градиент целевой функции
, построить его.
- Провести линию уровня целевой функции, перпендикулярную градиенту.
- Перемещать линию уровня параллельно самой себе в направлении
, найти точку
, в которой f достигает максимума (минимума).
- Найти координаты
, решая систему уравнений прямых, пересекающихся в точке оптимума, вычислить
.
В случае непустого множества допустимых решений возможны три типовых ситуации:
- задача имеет единственное решение (линия уровня касается множества допустимых решений в одной точке);
- задача имеет бесконечное множество решений (линия уровня касается множества допустимых решений вдоль стороны многоугольника);
- задача не имеет решения (множество допустимых решений не ограничено).
Пример 1. Решить задачу линейного программирования 







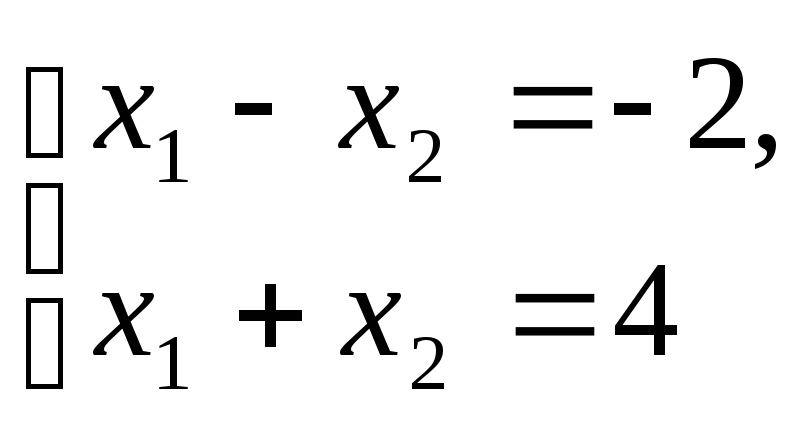

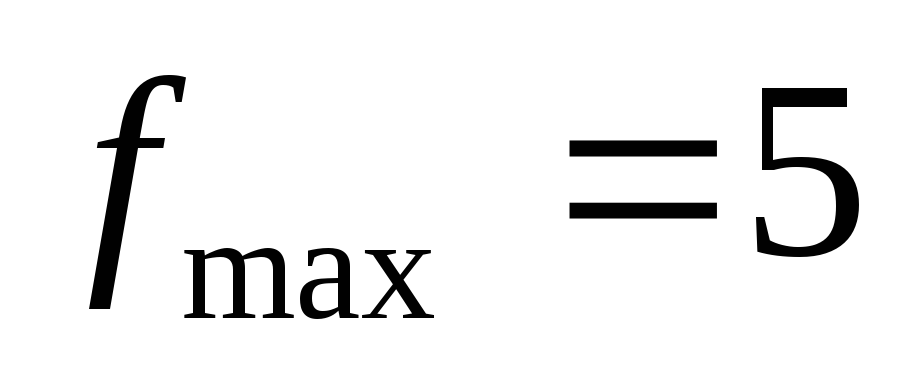
Для продолжения скачивания необходимо пройти капчу:
Применение графического метода для решения задач линейного программирования
Методы решения задач линейного программирования в зависимости от размерности задачи оптимизации подразделяются на графические и аналитические [1,2,7]. Графический метод оптимизации применяется только для двумерных задач, когда решение можно представить на плоскости. Это позволяет получить наглядное представление об оптимизационном решении задачи, что является основным достоинством метода. Но возможности применения метода ограничены, он может использоваться для простейших математических моделей на отдельных этапах анализа сложных оптимизационных процессов. Рассмотрим применение графического метода на примере задачи рационального распределения ресурсов. Условие задачи, связанной с рациональным использованием топлива на тепловых станциях энергосистемы для получения максимального суммарного отпуска электроэнергии, и исходные данные для простейшего случая двумерной задачи, представлены в табл.2.1 (численные значения параметров носят условный характер и определяются удобством проведения расчетов). Математическая модель задачи рационального распределения ресурсов включает в себя целевую функцию (2.2), ограничения (2.3-2.4) и граничные условия (2.5). Математически требуется найти решение W1,W2, удовлетворяющее системе неравенств (2.3-2.5), соответствующее максимуму F. Алгоритм графического метода сводится к следующим этапам:
- Построение области допустимых решений (ОДР):
- отобразим графически на плоскости неравенство (2.3), для этого перейдем к уравнению вида:

- аналогичные построения проведем для неравенства (2.4) – линия (2) рис.2.1 по точкам (W1=1400,W2=0) и (W1=0, W2=700);
- граничные условия соответствуют двум дополнительных неравенствам (2.5), которые определяют неотрицательность переменных W1 и W2, что отображено штриховкой на рис 2.1.
Координаты всех точек не заштрихованного многоугольника ABCO имеют такие значения W1 и W2, которые удовлетворяют системе неравенств (2.3-2.5) и образуют область допустимых решений.
- Построение графика целевой функции.
Графически видно, что оптимизационная задача имеет множество допустимых решений, из которых требуется найти оптимальное, удовлетворяющее в данном случае максимуму целевой функции. Для графического представления целевой функции зададимся произвольным значением F=12000 и построим линию (3), которая называется линией уровня целевой функции (рис.2.1): 
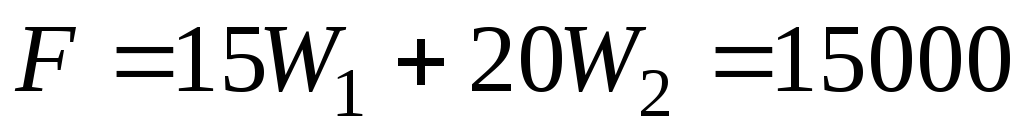
 , построить его.
, построить его. , найти точку
, найти точку , в которой f достигает максимума (минимума).
, в которой f достигает максимума (минимума).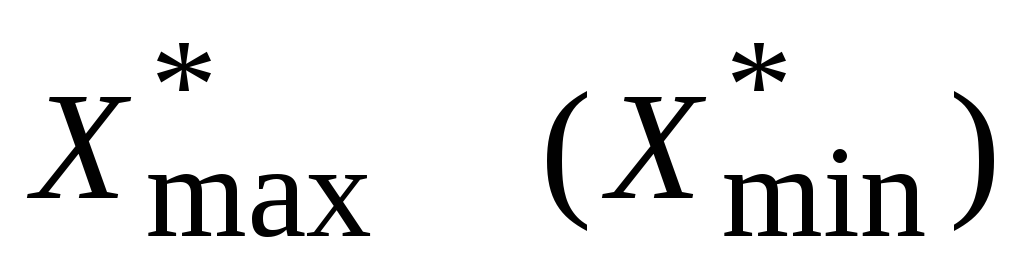 , решая систему уравнений прямых, пересекающихся в точке оптимума, вычислить
, решая систему уравнений прямых, пересекающихся в точке оптимума, вычислить 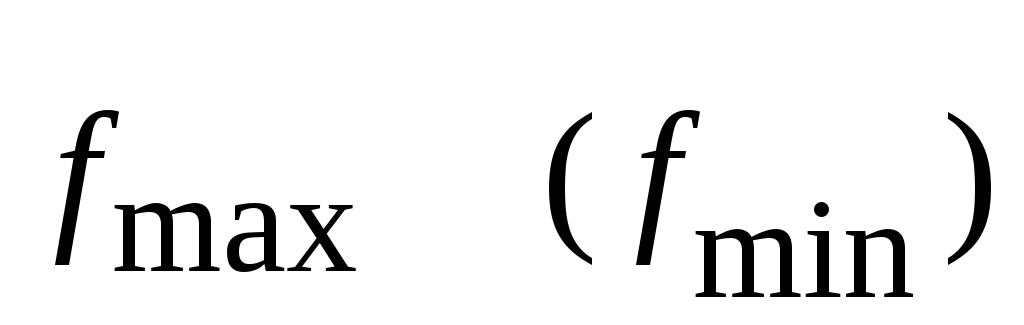 .
.







