Градиентные методы решения задачи нелинейного программирования

Градиентные методы решения задач нелинейного программирования

Градиентные методы позволяют находить приближенное решение любой задачи нелинейного программирования. Однако в общем случае это будет точка локального экстремума. Поэтому более целесообразно использовать градиентные методы для нахождения решения задач выпуклого программирования, в которых локальный экстремум является одновременно и глобальным.

Процесс нахождения решения задачи с помощью градиентных методов состоит в том, что начиная с некоторой точки осуществляется последовательный переход к некоторым другим точкам до тех пор, пока градиент целевой функции в очередной точке не станет равным нулю, или не будет выполнено условие , где ε характеризует точность полученного решения.

Наиболее распространенными из градиентных методов являются методы приведенного градиента Вулфа, штрафных функций и Эрроу−Гурвица.

5.4.1 Метод приведенного градиента Вулфа

Пусть требуется минимизировать целевую функцию

где матрица А − матрица порядка m×n и ранга m, b − вектор из Е_m, функция f непрерывно дифференцируема в Е_n.

Заметим, что ограничения (5.26) линейные. Предположим, что А невырожденная матрица, а x — допустимая точка. Матрицу А можно представить в виде , а вектор − в виде , где В – неособенная матрица порядка m×m. Вектор x_B называется базисным, и его компоненты строго положительны. Компоненты внебазисного вектора могут быть либо положительными, либо нулевыми.

Пусть , где − градиент функции f по переменным базисного вектора , а − градиент f по внебазисным переменным . Направление является направлением спуска и возможным для функции f в точке , если и , если . Определим вектор , обладающий этими свойствами. Представим вектор в виде . Равенство =0 выполняется, если для любого положить .

Пусть − приведенный градиент. Исследуем .

Мы должны выбрать вектор так, чтобы и , если . Для этого принимается следующее правило. Для каждой внебазисной компоненты j положим , если , и положим , если r_j>0. Из этого следует выполнение неравенства , если . Кроме того, и строгое неравенство имеет место, если .

Здесь вектор в том и только том случае, если седловая точка Куна−Таккера.

В целях сокращения записей символ, означающий транспонирование опущен.

Алгоритм метода приведенного градиента.

Пусть имеем задачу (5.26). Предположим, что любые m столбцов матрицы А линейно независимы и что каждая экстремальная точка допустимой области (5.26) имеет m строго положительных компонент. Указанный алгоритм сходится к точке Куна−Таккера при условии, что в качестве базисных переменных выбраны m наибольших положительных переменных.

Выбрать точку , удовлетворяющую условиям . Положить k=1 и перейти к основному этапу.

Шаг 1. Положить , где и получаются из формул (5.30) и (5.31) соответственно. Если , то остановиться; − оптимальная точка (точка Куна − Таккера). В противном случае перейти к шагу 2.

I_k − множество индексов m наибольших компонент вектора , (5.27)

Шаг 2. Решить следующую задачу одномерной минимизации:

Здесь – j-е компоненты векторов и .

Положим λ_k равным оптимальному и . Заменить k на k+1 и перейти к шагу 1.

В качестве начальной точки выберем .

Информацию по каждой итерации будем представлять в виде таблицы, подобной симплекс-таблице.

В точке имеем . В соответствии с (5.27) множество I₁=, так что B=[a₃,a₄] и D=[a₁,a₂] (согласно (5.28)). Согласно (5.29) приведенный градиент

Результаты вычислений будем помещать в таблицу 5.2.

В соответствии с (5.30) имеем . По формуле (5.31) . Получим

, , . Тогда . Вектор направления, таким образом, равен .

При начальной точке минимизируем целевую функцию по направлению . Максимальное значение λ, для которого точка допустима, вычисляется в соответствии с (5.32) и равно

Значение целевой функции в точке

так что задача линейного поиска имеет вид:

Поиск направления. В точке в соответствии с (5.27) имеем

В соответствии с (5.29) имеем

Тогда, согласно (5.30) имеем, что

Таким образом, вектор направления равен

Начиная процедуру из точки , минимизируем целевую функцию по направлению . Максимальное значение λ, для которого точка допустима, равно

Значение целевой функции в точке , так что находится из решения задачи.

Теперь I₃=, то есть B=[a₁,a₂] и D=[a₃,a₄]. Имеем

Отсюда , . Следовательно, и решение оптимально.

Таблица 5.2 – Результаты вычислений методом градиента Вулфа

Решение	0	0	2	5	0,0
-4	-6	0	0
1 1	1 5	1 0	0 1
-4	-6	0	0
Решение	0	-6,436
0	0
1 0	0 1
0	0
Решение	0	-7,16
0	0
1 0	0 1
0	0	0	1

5.4.2 Метод штрафных функций

Для определенности рассмотрим задачу нахождения максимального значения вогнутой функции при условиях , где g_i – выпуклые функции. Заметим, что здесь функции g_i могут быть как линейными, так и нелинейными. Однако в первом случае удобнее использовать метод приведенного градиента Вулфа, что существенно сокращает вычисления.

Вместо непосредственного решения вышеприведенной задачи, находят максимальное значение функции

= + , являющейся суммой целевой функции задачи, и некоторой функции Н, определяемой системой ограничений и называемой штрафной функцией. Штрафную функцию записываем в виде:

а − некоторые постоянные числа, называемые весомыми коэффициентами.

Используя штрафную функцию, последовательно переходят от одной точки к другой до тех пор, пока не получат приемлемое решение. При этом координаты последующей точки находят по формуле

Из соотношения (5.34) следует, что если предыдущая точка находится в области допустимых решений исходной задачи, то второе слагаемое в квадратных скобках равно нулю и переход к последующей точке определяется только градиентом целевой функции.

Если же указанная точка не принадлежит области допустимых решений, то за счет данного слагаемого на последующих итерациях достигается возвращение в область допустимых решений. При этом значении должны быть маленькими.

Алгоритм метода штрафных функций.

Процесс нахождения решения задачи выпуклого программирования включает следующие этапы:

1. Определяют исходное допустимое решение.

2. Задают точность вычислений (штрафной параметр λ).

3. Находят по всем переменным частные производные от целевой функции и функций, определяющих область допустимых решений задачи.

4. По формулам (5.34) находят координаты точки, определяющей возможное новое решение задачи.

5. Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переходят к следующему этапу. Если координаты найденной точки удовлетворяют системе ограничений, то исследуют необходимость перехода к последующему допустимому решению. В случае такой необходимости переходят к этапу 2, в противном случае найдено решение задачи с заданной точностью.

6. Устанавливают значение весовых коэффициентов и переходят к этапу 4.

Найти максимальное значение функции

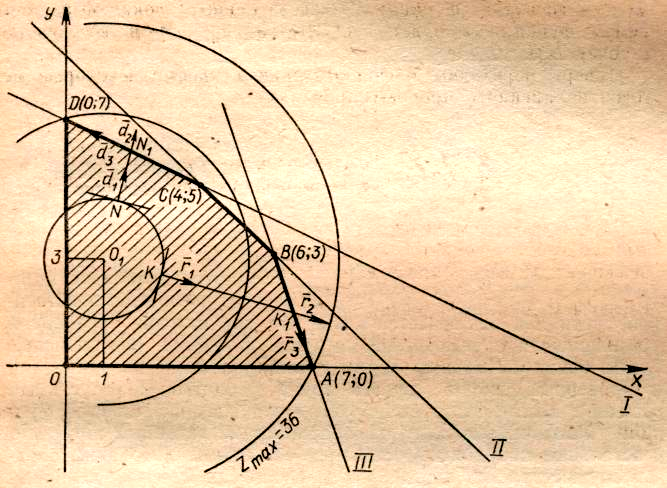
Целевая функция данной задачи представляет собой отрицательно−определенную квадратичную форму, а ограничения – выпуклую область. Следовательно, имеем задачу выпуклого программирования. Построим область допустимых решений задачи и линии уровня (рисунок 5.5). Точка касания одной из этих окружностей с областью допустимых решений и является искомой точкой максимума целевой функции.

Рисунок 5.5 – Область допустимых значений

В качестве начальной точки возьмем x (0) =(6,7) и положим λ=0,1. Определим частные производные:

Далее, используя формулу (5.34), построим последовательность точек для определения приемлемого решения.

Так как точка x (0) =(6,7) принадлежит области допустимых решений, то

Найдем . Так как , то точка принадлежит допустимой области. В этой точке значение целевой функции .

Точка не принадлежит допустимой области. Следовательно

Здесь возникает вопрос о выборе весового коэффициента a. Выберем его так, чтобы точка не слишком далеко удалилась от границы допустимой области и вместе с тем принадлежала этой области. Этим требованиям удовлетворяет . Тогда ; ; ; .

Результаты вычислений приведены в таблице 5.3.

Таблица 5.3 – Результаты вычислений методом штрафных функций

K
1	(4,8; 5,6)	11,2	-54,4
2	(3,84; 4,48)	1,664	-34,816
3	(3,072; 3,584)	-9,0981
4	(3,950; 4,165)	0,660	-32,950
5	(3,16; 3,332)	-10,2
6	(3,987; 4,059)	0,272	-32,372
7	(3,189; 3,247)	-2,715
8	(3,999; 4,027)	-0,137	-32,185
9	(3,199; 3,219)	-10,744
10	(4,004; 4,012)	0,096	-32,128
11	(3,203; 3,210)	-10,781
12	(4,005; 4,008)	0,078	-32,104

Сравнивая значения целевой функции, полученные в 10-й и 12-й итерациях, видим, что они совпадают с точностью до 10 -1 . Это говорит о близости точки к точке максимума целевой функции. Исследуем теперь градиенты функций и в точке :

Вычислим отношения одноименных координат векторов: . Следовательно, векторы и практически коллинеарны. Полученное решение при необходимости можно уточнить дальнейшими шагами до полной коллинеарности градиентов целевой и ограничительной функций.

В заключении заметим, что на практике используются несколько вариантов штрафных функций, а также то, что решение сложных задач нелинейного программирования градиентными методами связано с большим объемом вычислений и целесообразно только с использованием ЭВМ.

Дата добавления: 2018-04-04 ; просмотров: 2103 ; Мы поможем в написании вашей работы!

Источник

§4. Градиентный метод нелинейного программирования.

Пусть мы имеем некоторую функцию двух действительных переменных и некоторую точкуA, принадлежащую области определенияXэтой функции. Назовем градиентом функцииfвектор(символчитается: «набла»).

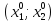
Градиент в точке А перпендикулярен касательной к линии уровня функции

в этой точке. Например дана функция . Построим несколько ее линий уровня (рис. 55):

Известно, что направление градиента служит направлением максимальной скорости роста функции. На примере задачи с двумя переменными покажем геометрическую картину градиентного метода.

Задача 7.6.1. Найти глобальный максимум на множестве решений системы неравенств.

Предположим, что мы начинали с некоторого допустимого решения, определённого координатами точки . Градиентилиявляется вектором, перпендикулярным касательной к линии уровня в точке. Мы двигаемся из точкив направлениидо тех пор, пока не достигнем границы множества допустимых решений. Дальше мы не можем двигаться в направлении, так как при этом мы выйдем из множества допустимых решений. Поэтому мы выбираем вектор, составляющий с векторомнаименьший угол по сравнению с любым другим вектором с началом в точкеи лежащим в множестве допустимых решений. Таким образом, на следующем шаге мы двигаемся вдоль прямойЭто приводит нас в точкуНа этом процесс заканчивается. Геометрически это выражается тем, чтосоставляет тупой угол с любым вектором в множестве допустимых решений, выходящим из точки А.Заметим что в точке функция достигает глобального максимума:Предположим теперь, что, решая эту же задачу, в качестве начального допустимого решения мы выберем точку(рис. 56). В этом случае мы сначала по направлениюдостигаем точки, а затем по направлениювдоль прямойпопадаем в точку. На этом процесс заканчивается:В точкефункция достигает лишь локального максимума. Даже на одном примере видно, что результат решения зависит от того, с какой точки допустимого решения начинается процесс.

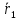
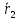
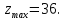
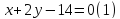
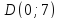
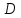
Градиентные методы в лучшем случае обычно сходятся лишь к локальному минимуму. Впрочем бывает и так, что даже такая сходимость отсутствует.

Только в том случае, когда задача обладает подходящими свойствами выпуклости или вогнутости, можно быть уверенным, что процесс сходиться к глобальному экстремуму.

Рассмотрим далее идею метода обхода узлов пространственной сетки. Он заключается в том, что для каждой переменной устанавливается определенный интервал изменения (шаг поиска). Затем берем начальную точку с минимальными координатами и проверяем, входит ли эта точка в множество допустимых решений. После этого вычисляем в ней значение целевой функции. Увеличиваем одну из координат на заданный интервал, а остальные координаты оставляем без изменения. Таким образом осуществляется передвижение вдоль одной оси на величину шага. Для новой точки тоже проверяем ее принадлежность множеству Ω и вычисляем значение целевой функции. Опять увеличиваем на интервал ту же координату и испытываем полученную точку и т.д. Дойдя до границы множества Ω, изменяем на величину шага другую координату, т. е. смещаемся в сторону, и снова от некоторой начальной точки двигаемся до границы области и т.д. (рис. 57). Здесь значениям переменных

геометрически соответствуют параллельные гиперплоскости, отстоящие друг от друга на величину шага . Число систем таких плоскостей равно числу переменных. В пересечениях они образуют точки — узлы пространственной сетки. В процессе поиска мы обходим поочередно узлы, принадлежащие многограннику допустимых планов, и вычисляем в каждом случае значение целевой функции. Наибольшее (наименьшее) из них указывает с точностью до шага оптимальную точку.Этот метод, как нетрудно было уже заметить, связан с ог­ромным объемом вычислительной работы. Он пригоден для ре­шения задач с малым числом переменных и с обязательным применением электронных вычислительных машин.

Источник