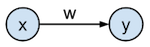Gradient descent regression python

How to implement a neural network (1/5) — gradient descent

This page is the first part of this introduction on how to implement a neural network from scratch with Python and NumPy. This first part will illustrate the concept of gradient descent illustrated on a very simple linear regression model. The linear regression model will be approached as a minimal regression neural network. The model will be optimized using gradient descent, for which the gradient derivations are provided.

This is the first part of a 5-part tutorial on how to implement neural networks from scratch in Python:

Gradient descent for linear regression

In what follows we will go into the details of gradient descent illustrated on a very simple network: a 1-input 1-output linear regression model that has the goal to predict the target value $t$ from the input value $x$. The network is defined as having an input $\mathbf$ which gets transformed by the weight $w$ to generate the output $\mathbf$ by the formula $\mathbf = w \cdot \mathbf$, and where $\mathbf$ needs to approximate the targets $\mathbf$ as good as possible as defined by a loss function. This network can be represented graphically as:

In practice, we typically have multiple layers, non-linear activation functions, and a bias for each node. In this tutorial, we only have one layer with one weight parameter $w$, no activation function on the output, and no bias. We will discuss hidden layers in part 3 of this series.

We will approximate the targets $\mathbf$ with the outputs of the model $y$ by minimizing the squared error between target and output. This minimization will be performed by the gradient descent optimization algorithm which is typically used in training of neural networks.

# Imports %matplotlib inline %config InlineBackend.figure_formats = ['svg'] import numpy as np # Matrix and vector computation package import matplotlib import matplotlib.pyplot as plt # Plotting library import seaborn as sns # Fancier plots # Set seaborn plotting style sns.set_style('darkgrid') # Set the seed for reproducability np.random.seed(seed=13) # 

Generating a toy dataset

In this example, the targets $\mathbf$ will be generated from a function $f$ and additive Gaussian noise sampled from $\mathcal(0, 0.2)$, where $\mathcal$ is the normal distribution with mean 0 and variance 0.2. $f$ is defined as $f(x) = 2 x$, with $\mathbf$ the input samples, slope $2$ and intercept $0$. $\mathbf$ is $f(\mathbf) + \mathcal(0, 0.2)$.

We will sample 20 input samples $\mathbf$ from the uniform distribution between 0 and 1, and then generate the target output values $\mathbf$ by the process described above. These resulting inputs $\mathbf$ and targets $\mathbf$ are plotted against each other in the figure below together with the original $f(x)$ line without the gaussian noise. Note that $\mathbf$ is a vector of individual input samples $x_i$, and that $\mathbf$ is a corresponding vector of target values $t_i$.

# Define the vector of input samples as x, with 20 values # sampled from a uniform distribution between 0 and 1 x = np.random.uniform(0, 1, 20) # Generate the target values t from x with small gaussian noise # so the estimation won't be perfect. # Define a function f that represents the line that generates t # without noise. def f(x): return x * 2 # Create the targets t with some gaussian noise noise_variance = 0.2 # Variance of the gaussian noise # Gaussian noise error for each sample in x noise = np.random.randn(x.shape[0]) * noise_variance # Create targets t t = f(x) + noise # 

# Plot the target t versus the input x plt.figure(figsize=(5, 3)) plt.plot(x, t, 'o', label='$t$') # Plot the initial line plt.plot([0, 1], [f(0), f(1)], 'b--', label='$f(x)$') plt.xlabel('$x$', fontsize=12) plt.ylabel('$t$', fontsize=12) plt.axis((0, 1, 0, 2)) plt.title('inputs (x) vs targets (t)') plt.legend(loc=2) plt.show() # 

Define the loss function

We will optimize the model $\mathbf = \mathbf * w$ by tuning parameter $w$ so that the mean squared error (MSE) along all samples is minimized. The function to minimizize is also known as the loss (or cost) function .

The mean squared error is defined as $\xi = \frac \sum_^ \Vert t_i — y_i \Vert ^2$, with $N$ the number of samples in the training set. This corresponds to the average Euclidian distance between the output and corresponding targets. The optimization goal is thus: $\underset> \frac \sum_^ \Vert t_i — y_i \Vert^2$.
Notice that we take the mean of errors over all samples, which is known as batch training. We could also update the parameters based upon one sample at a time, which is known as online training.

This loss function for variable $w$ is plotted in the figure below. The value $w=2$ is at the minimum of the loss function (bottom of the parabola), this value is the same value as the slope we choose for $f(x)$. Notice that this function is convex and that there is only one minimum: the global minimum. While every squared error loss function for linear regression is convex, this is not the case for other models and other loss functions.

The neural network model is implemented in the nn(x, w) function, and the loss function is implemented in the loss(y, t) function.

def nn(x, w): """Output function y = x * w""" return x * w def loss(y, t): """MSE loss function""" return np.mean((t - y)**2) 

# Plot the loss vs the given weight w # Vector of weights for which we want to plot the loss ws = np.linspace(0, 4, num=100) # weight values # loss for each weight in ws loss_ws = np.vectorize(lambda w: loss(nn(x, w) , t))(ws) # Plot plt.figure(figsize=(5, 3)) plt.plot(ws, loss_ws, 'r--', label='loss') plt.xlabel('$w$', fontsize=12) plt.ylabel('$\\xi$', fontsize=12) plt.title('loss function with respect to $w$') plt.xlim(0, 4) plt.legend() plt.show() # 

Источник

Implementing Linear Regression Using Gradient Descent in Python

In the previous article, we looked at the theory behind linear regression. In this article, we will implement the linear regression algorithm from scratch and understand the various steps involved.

In my earlier article, I used the in-built function in scikit-learn to predict the houses’ prices. Towards the end of the article, we will compare the two approaches and reason for the outputs.

Prerequisites

Introduction

Linear regression is a type of supervised learning algorithm. It is used in many applications, such as in the financial industry. First, let’s understand the various functions needed to implement a linear regression class, to begin with the coding aspect.

Code structure

We define the following methods in the class Regressor :

1. __init__ : In the __init__ method, we initialize all the parameters with default values. These parameters are added as and when required. For now, you will see that all the parameters are initialized beforehand. But while coding, you create new variables as and when needed.
2. initialize_weights_and_bias : In the initialize_weights_and_bias method, the weights and biases are initialized. We use random initialization to initialize the weights, and the bias is initially 0.
3. computeError : This function calculates the error or loss function and returns the cost. The input to this function is the predicted output and the actual output.
4. optimize : This function uses stochastic gradient descent to optimize the loss function. We initially compute the gradients of the weights and the bias in the variables dW and db. Using these gradients, we updated our weights and biases iteratively.
5. normalize : This function subtracts the mean from the data and divides it by its standard deviation. This ensures the data is centered around 0, and the standard deviation is always 1. Data with such distribution is easier to work with and results in the model learning better. This is because various features have various scales. The larger values may end up contributing more to the output. Hence, normalization ensures no such anomalies take place.
6. fit : The fit method calls all the above functions. In this method, we perform normalization on the input features and compute the loss. Once the loss is computed, we optimize the loss function by applying the optimize function on the input-output pair. We perform this until there is no significant change in the loss values obtained after training.
7. predict : This function is used to test the model on unseen data. The input to the function is the input data. The predict function outputs the dependent variable.
8. plot : In this method, we plot the loss function versus the number of iterations.
9. score : This function calculates the accuracy. The accuracy is computed using the following formula: $$ accuracy = \frac<(y - \hat)^2>^n(y-\bar)^2>$$

Code

Let us put together the information we collected above and create the Regressor class.

import numpy as np import matplotlib.pyplot as plt # Define Regressor class class Regressor():  # init methodd initializes all parameters needed to implement regression  def __init__(self, learning_rate=0.01, tol=0.01, seed=None,normalize=False):  self.W = None  self.b = None  self.__lr = learning_rate  self.__tol = tol  self.__length = None  self.__normalize = normalize  self.__m = None  self.__costs = []  self.__iterations = []  np.random.seed(seed if seed is not None else np.random.randint(100))  # random initialization of weights and bias  def __initialize_weights_and_bias(self):  self.W = np.random.randn(self.__length) #(n,1)  self.b = 0  # compute the error function: sum of squared errors  def __computeCost(self,h,Y):  loss = np.square(h-Y)  cost = np.sum(loss)/(2*self.__m)  return cost  # implement optimization function  def __optimize(self,X,Y):  h = np.dot(X,self.W)+self.b  dW = np.dot( X.T, (h-Y) ) / self.__m  db = np.sum( h-Y ) / self.__m  self.W = self.W - self.__lr*dW  self.b = self.b - self.__lr*db  # normalize the dataset by subtracting the mean and dividing by std deviation  def __normalizeX(self,X):return (X-self.__mean) / (self.__std)  # fit the model to the dataset: training process  def fit(self, X, y, verbose=False):  if self.__normalize:  self.__mean, self.__std = X.mean(axis=0), X.std(axis=0)  X = self.__normalizeX(X)  self.__m,self.__length = X.shape  self.__initialize_weights_and_bias()  last_cost,i = float('inf'),0  while True:  h = np.dot(X,self.W)+self.b  cost = self.__computeCost(h,y)  if verbose: print(f"Iteration: i>, Cost: cost:.3f>")  self.__optimize(X,y)  if last_cost-cost  self.__tol: break  else: last_cost,i = cost,i+1  self.__costs.append(cost)  self.__iterations.append(i)  # test the model on test data  def predict(self,X):   if self.__normalize: X = self.__normalizeX(X)  return np.dot(X,self.W)+self.b  # plot the iterations vs cost curves  def plot(self,figsize=(7,5)):  plt.figure(figsize=figsize)  plt.plot(self.__iterations,self.__costs)  plt.xlabel('Iterations')  plt.ylabel('Cost')  plt.title("Iterations vs Cost")  plt.show()  # calculates the accuracy  def score(self,X,y):  return 1-(np.sum(((y-self.predict(X))**2))/np.sum((y-np.mean(y))**2)) 

Test the code

We use the Boston housing dataset to test the performance of the model built. The code to call the Boston housing dataset and to train the model is given below.

# load the boston housing dataset from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split  data = load_boston() # split the dataset into train and test sets X_train, X_test, y_train,y_test = train_test_split(data.data, data.target,test_size=0.1) # print train and test set shapes print(f"X_train:X_train.shape>\ny_train:y_train.shape>") # normalize the dataset and instantiate Regressor object regressor = Regressor(normalize=True) # call the fit method regressor.fit(X_train,y_train)  train_score = regressor.score(X_train,y_train) test_score = regressor.score(X_test,y_test)  print("Train Score:", train_score) print("Test Score: ",test_score) regressor.plot() 

Output analysis

We get a training accuracy of about 71%, and test accuracy stands at 65%. A fun exercise would be to set normalize to False and try the same code. Check the train and test accuracies. You will understand the significance of normalization.

Train Score: 0.7142761537090165 Test Score: 0.6504432415059116 

Comparison with scikit learn

The training and test accuracy obtained using the library stand at 93% and 79.29%, respectively. We conclude that the data requires some non-linearity to be introduced, and polynomial regression would probably work much better than linear regression.

Conclusion

In this article, we implemented the linear regression from scratch using numpy. This should give you an idea about converting mathematical equations into Pythonic code. Implementing machine learning algorithms from scratch enhances one’s understanding of the subject.

Источник