Генерация выборки нормального распределения python

Python для анализа данных¶

Нам пригодится только модуль scipy.stats . Полное описание доступно по ссылке. По ссылке можно прочитать полную документацию по работе с непрерывными (Continuous), дискретными (Discrete) и многомерными (Multivariate) распределениями. Пакет также предоставляет некоторое количество статистических методов, которые рассматриваются в курсах статистики.

import scipy.stats as sps import numpy as np import ipywidgets as widgets import matplotlib.pyplot as plt %matplotlib inline

1. Работа с библиотекой scipy.stats .¶

• X(params).rvs(size=N) — генерация выборки размера $N$ (Random VariateS). Возвращает numpy.array ;
• X(params).cdf(x) — значение функции распределения в точке $x$ (Cumulative Distribution Function);
• X(params).logcdf(x) — значение логарифма функции распределения в точке $x$;
• X(params).ppf(q) — $q$-квантиль (Percent Point Function);
• X(params).mean() — математическое ожидание;
• X(params).median() — медиана ($1/2$-квантиль);
• X(params).var() — дисперсия (Variance);
• X(params).std() — стандартное отклонение = корень из дисперсии (Standard Deviation).

Кроме того для непрерывных распределений определены функции

• X(params).pdf(x) — значение плотности в точке $x$ (Probability Density Function);
• X(params).logpdf(x) — значение логарифма плотности в точке $x$.

• X(params).pmf(k) — значение дискретной плотности в точке $k$ (Probability Mass Function);
• X(params).logpdf(k) — значение логарифма дискретной плотности в точке $k$.

Все перечисленные выше методы применимы как к конкретному распределению X(params) , так и к самому классу X . Во втором случае параметры передаются в сам метод. Например, вызов X.rvs(size=N, params) эквивалентен X(params).rvs(size=N) . При работе с распределениями и случайными величинами рекомендуем использовать первый способ, посколько он больше согласуется с математическим синтаксисом теории вероятностей.

Параметры могут быть следующими:

• loc — параметр сдвига;
• scale — параметр масштаба;
• и другие параметры (например, $n$ и $p$ для биномиального).

Для примера сгенерируем выборку размера $N = 200$ из распределения $\mathcal(1, 9)$ и посчитаем некоторые статистики. В терминах выше описанных функций у нас $X$ = sps.norm , а params = ( loc=1, scale=3 ).

Примечание. Выборка — набор независимых одинаково распределенных случайных величин. Часто в разговорной речи выборку отождествляют с ее реализацией — значения случайных величин из выборки при «выпавшем» элементарном исходе.

sample = sps.norm(loc=1, scale=3).rvs(size=200) print('Первые 10 значений выборки:\n', sample[:10]) print('Выборочное среденее: %.3f' % sample.mean()) print('Выборочная дисперсия: %.3f' % sample.var()) 

Первые 10 значений выборки: [ 0.65179639 -0.66437884 0.61450407 -0.1828078 0.42271419 0.14424901 2.01547486 7.81094724 -1.35246891 -1.35574313] Выборочное среденее: 0.854 Выборочная дисперсия: 9.118

Источник

numpy.random.normal#

Draw random samples from a normal (Gaussian) distribution.

The probability density function of the normal distribution, first derived by De Moivre and 200 years later by both Gauss and Laplace independently [2], is often called the bell curve because of its characteristic shape (see the example below).

The normal distributions occurs often in nature. For example, it describes the commonly occurring distribution of samples influenced by a large number of tiny, random disturbances, each with its own unique distribution [2].

New code should use the normal method of a Generator instance instead; please see the Quick Start .

Mean (“centre”) of the distribution.

scale float or array_like of floats

Standard deviation (spread or “width”) of the distribution. Must be non-negative.

size int or tuple of ints, optional

Output shape. If the given shape is, e.g., (m, n, k) , then m * n * k samples are drawn. If size is None (default), a single value is returned if loc and scale are both scalars. Otherwise, np.broadcast(loc, scale).size samples are drawn.

Returns : out ndarray or scalar

Drawn samples from the parameterized normal distribution.

probability density function, distribution or cumulative density function, etc.

which should be used for new code.

The probability density for the Gaussian distribution is

where \(\mu\) is the mean and \(\sigma\) the standard deviation. The square of the standard deviation, \(\sigma^2\) , is called the variance.

The function has its peak at the mean, and its “spread” increases with the standard deviation (the function reaches 0.607 times its maximum at \(x + \sigma\) and \(x — \sigma\) [2]). This implies that normal is more likely to return samples lying close to the mean, rather than those far away.

P. R. Peebles Jr., “Central Limit Theorem” in “Probability, Random Variables and Random Signal Principles”, 4th ed., 2001, pp. 51, 51, 125.

Draw samples from the distribution:

>>> mu, sigma = 0, 0.1 # mean and standard deviation >>> s = np.random.normal(mu, sigma, 1000) 

Verify the mean and the variance:

>>> abs(mu - np.mean(s)) 0.0 # may vary 

>>> abs(sigma - np.std(s, ddof=1)) 0.1 # may vary 

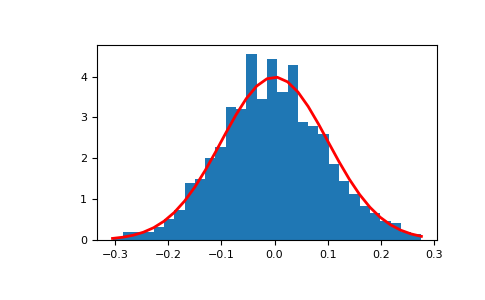
Display the histogram of the samples, along with the probability density function:

>>> import matplotlib.pyplot as plt >>> count, bins, ignored = plt.hist(s, 30, density=True) >>> plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) * . np.exp( - (bins - mu)**2 / (2 * sigma**2) ), . linewidth=2, color='r') >>> plt.show() 

Two-by-four array of samples from the normal distribution with mean 3 and standard deviation 2.5:

>>> np.random.normal(3, 2.5, size=(2, 4)) array([[-4.49401501, 4.00950034, -1.81814867, 7.29718677], # random [ 0.39924804, 4.68456316, 4.99394529, 4.84057254]]) # random 

Источник

Метод numpy.random.normal() — случайные выборки в Python

Функция numpy.random.normal() выполняет случайные выборки и генерирует случайные значения из нормального (гауссовского) распределения в Python.

Нормальное распределение часто называют кривой нормального распределения из-за его формы. Поскольку форма графика нормального распределения похожа на колокол, его часто называют кривой колокола.

Синтаксис

Аргументы

1. loc: Это среднее значение нормального распределения. Его также называют средним. Если в аргументе ничего не передается, он автоматически принимает 0 в качестве среднего значения для нормального распределения. Потому что если получается нормальное распределение, то среднее значение равно 0; поэтому 0.0 назначается по умолчанию.
2. scale: Это стандартное отклонение нормального распределения. Его также называют стандартным отклонением. Как следует из названия, это стандартное отклонение между точками нормального распределения. Если в качестве аргумента передается стандартное отклонение, функция автоматически присваивает значение 1,0.
3. size: это количество отрисовываемых образцов. Если n — количество выборок, переданных в аргументе, то выбирается n выборок. Если в аргументе ничего не указано, будет взята 1 выборка.

Пример 1 numpy.random.normal()

В этой программе мы импортировали пакет numpy, состоящий из нескольких функций. Мы использовали функцию random.normal(). Это функция, присутствующая внутри случайного класса пакета numpy. Функция np.random.normal() находит нормальное распределение для случайных выборок.

Пример 2

В этой программе мы создали три переменные: mu, sigma и siz.

mu используется для хранения среднего значения нормального распределения. Sigma используется для хранения стандартного отклонения. А siz используется для хранения количества выборок.

Мы передали функции среднее значение, стандартное отклонение и размер. Следовательно, на выходе будет семь выборок, поскольку мы указали семь в качестве размера.

Автор статей и разработчик, делюсь знаниями.

Источник

Модуль random. Часть 3

Рассмотрим равномерное и нормальное распределения непрерывной случайной величины.

• Непрерывное вероятностное распределение
  • Непрерывное равноемерное распределение
    • Плотность вероятности
    • Матожидание и дисперсия
    • Реализация на Питоне
    • Разница между np.random.random(), np.random.rand() и np.random.uniform()
    • Функция плотности нормального распределения
    • Функция np.random.normal()
    • Расчет вероятности
    • Функция плотности и функция распределения
    • Вероятность конкретного значения
    • Формирование выборки
    • Центральная предельная теорема
      • Определения и нотация
      • ЦПТ и нормальное распределение
      • Проверим на Питоне
      • Способ 1. График нормальной вероятности
      • Способ 2. Тест Шапиро-Уилка
      • Поправка на непрерывность распределения
      • Пример приближения

      Непрерывное вероятностное распределение

      Как уже было сказано, в отличие от дискретной величины, непрерывная величина может принимать любое значение в заданном интервале.

      Непрерывное равноемерное распределение

      Непрерывное равномерное распределение (continuous uniform distribution) описывает случайную величину, вероятность значений которой одинакова на заданном интервале от a до b.

      Например, если мы знаем, что автобус приходит на остановку каждые 12 минут, то время ожидания автобуса на остановке равномерно распределено между 0 и 12 минутами.

      Плотность вероятности

      Непрерывное распределение (в отличие от дискретного) задается плотностью вероятности (probability density function, pdf). Для равномерного непрерывного распределения плотность вероятности задается вот такой несложной функцией.

      $$ pdf(x) = \begin \frac, x \in [a, b] \ 0, x \notin [a, b] \end $$

      В примере с ожиданием автобуса вероятность его приезда в любой момент в пределах заданного интервала равна

      $$ pdf(x) = \begin \frac = \frac, x \in [0, 12] \ 0, x \notin [0, 12] \end $$

      На графике равномерное распределение представляет собой прямоугольник, площадь которого всегда равна единице.

      

      Если мы хотим посчитать вероятность приезда автобуса в пределах заданного интервала ожидания, нам, по сути, нужно рассчитать отдельный участок площади прямоугольника.

      Например, вероятность приезда автобуса при ожидании до 12 минут включительно составляет 1.00 или 100%, потому что такой промежуток включает всю площадь прямоугольника.

      Теперь давайте рассчитаем вероятность ожидания автобуса до 7 минут включительно. Нас будет интересовать интервал от 0 до 7 минут и соответствующий участок площади прямоугольника.

      

      Применив несложную формулу, мы без труда вычислим площадь этого участка.

      $$ P(7) = \frac \times 7 \approx 0,583 $$

      Матожидание и дисперсия

      Остается рассчитать матожидание (среднее время ожидания автобуса) и дисперсию.

      Реализация на Питоне

      Воспользуемся функцией np.random.uniform() для того, чтобы создать равномерное распределение с параметрами U(0, 12).

      Источник