- std:: lgamma, std:: lgammaf, std:: lgammal
- Contents
- [edit] Parameters
- [edit] Return value
- [edit] Error handling
- [edit] Notes
- [edit] Example
- tgamma
- Parameters
- Return Value
- Example
- See also
- gamma_distribution Class
- Remarks
- Example
- Requirements
- gamma_distribution::gamma_distribution
- Parameters
- Remarks
- gamma_distribution::param_type
- Parameters
- Remarks
- std:: tgamma, std:: tgammaf, std:: tgammal
- [edit] Error handling
- [edit] Notes
- [edit] Example
std:: lgamma, std:: lgammaf, std:: lgammal
1-3) Computes the natural logarithm of the absolute value of the gamma function of num . The library provides overloads of std::lgamma for all cv-unqualified floating-point types as the type of the parameter. (since C++23)
Contents
[edit] Parameters
[edit] Return value
If no errors occur, the value of the logarithm of the gamma function of num , that is \(\log_| <\int_0^\infty t^
e | ∫ ∞
0 t num-1
e -t dt| , is returned.
If a pole error occurs, +HUGE_VAL , +HUGE_VALF , or +HUGE_VALL is returned.
If a range error due to overflow occurs, ±HUGE_VAL , ±HUGE_VALF , or ±HUGE_VALL is returned.
[edit] Error handling
Errors are reported as specified in math_errhandling .
If num is zero or is an integer less than zero, a pole error may occur.
If the implementation supports IEEE floating-point arithmetic (IEC 60559),
- If the argument is 1, +0 is returned.
- If the argument is 2, +0 is returned.
- If the argument is ±0, +∞ is returned and FE_DIVBYZERO is raised.
- If the argument is a negative integer, +∞ is returned and FE_DIVBYZERO is raised.
- If the argument is ±∞, +∞ is returned.
- If the argument is NaN, NaN is returned.
[edit] Notes
If num is a natural number, std :: lgamma ( num ) is the logarithm of the factorial of num — 1 .
The POSIX version of lgamma is not thread-safe: each execution of the function stores the sign of the gamma function of num in the static external variable signgam . Some implementations provide lgamma_r , which takes a pointer to user-provided storage for singgam as the second parameter, and is thread-safe.
There is a non-standard function named gamma in various implementations, but its definition is inconsistent. For example, glibc and 4.2BSD version of gamma executes lgamma , but 4.4BSD version of gamma executes tgamma .
The additional overloads are not required to be provided exactly as (A) . They only need to be sufficient to ensure that for their argument num of integer type, std :: lgamma ( num ) has the same effect as std :: lgamma ( static_cast < double >( num ) ) .
[edit] Example
#include #include #include #include #include // #pragma STDC FENV_ACCESS ON const double pi = std::acos(-1); // or std::numbers::pi since C++20 int main() { std::cout "lgamma(10) = " std::lgamma(10) ", log(9!) = " std::log(std::tgamma(10)) ", exp(lgamma(10)) = " std::exp(std::lgamma(10)) '\n' "lgamma(0.5) = " std::lgamma(0.5) ", log(sqrt(pi)) = " std::log(std::sqrt(pi)) '\n'; // special values std::cout "lgamma(1) = " std::lgamma(1) '\n' "lgamma(+Inf) = " std::lgamma(INFINITY) '\n'; // error handling errno = 0; std::feclearexcept(FE_ALL_EXCEPT); std::cout "lgamma(0) = " std::lgamma(0) '\n'; if (errno == ERANGE) std::cout " errno == ERANGE: " std::strerror(errno) '\n'; if (std::fetestexcept(FE_DIVBYZERO)) std::cout " FE_DIVBYZERO raised\n"; } lgamma(10) = 12.8018, log(9!) = 12.8018, exp(lgamma(10)) = 362880 lgamma(0.5) = 0.572365, log(sqrt(pi)) = 0.572365 lgamma(1) = 0 lgamma(+Inf) = inf lgamma(0) = inf errno == ERANGE: Numerical result out of range FE_DIVBYZERO raised
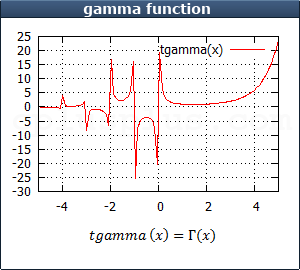
tgamma
Returns the gamma function of x .
Additional overloads are provided in this header ( ) for the integral types: These overloads effectively cast x to a double before calculations (defined for T being any integral type).
Parameters
Return Value
Gamma function of x .
If the magnitude of x is too large, an overflow range error occurs. If too small, an underflow range error may occur.
If x is zero or a negative integer for which the function is asymptotic, it may cause a domain error or a pole error (or none, depending on implementation).
If a domain error occurs:
— And math_errhandling has MATH_ERRNO set: the global variable errno is set to EDOM .
— And math_errhandling has MATH_ERREXCEPT set: FE_INVALID is raised.
If a range error occurs:
— And math_errhandling has MATH_ERRNO set: the global variable errno is set to ERANGE .
— And math_errhandling has MATH_ERREXCEPT set: either FE_OVERFLOW or FE_UNDERFLOW is raised.
If a pole error occurs:
— And math_errhandling has MATH_ERRNO set: the global variable errno is set to ERANGE .
— And math_errhandling has MATH_ERREXCEPT set: either FE_DIVBYZERO is raised.
Example
/* tgamma example */ /* printf */ /* tgamma */ int main () < double param, result; param = 0.5; result = tgamma (param); printf ("tgamma(%f) = %f\n", param, result ); return 0; >See also
lgamma Compute log-gamma function (function) erf Compute error function (function) erfc Compute complementary error function (function)
gamma_distribution Class
RealType
The floating-point result type, defaults to double . For possible types, see .
URNG
The uniform random number generator engine. For possible types, see .
Remarks
The class template describes a distribution that produces values of a user-specified floating-point type, or type double if none is provided, distributed according to the Gamma Distribution. The following table links to articles about individual members.
The property functions alpha() and beta() return their respective values for stored distribution parameters alpha and beta.
The property member param() sets or returns the param_type stored distribution parameter package.
The min() and max() member functions return the smallest possible result and largest possible result, respectively.
The reset() member function discards any cached values, so that the result of the next call to operator() does not depend on any values obtained from the engine before the call.
The operator() member functions return the next generated value based on the URNG engine, either from the current parameter package, or the specified parameter package.
For more information about distribution classes and their members, see .
For detailed information about the gamma distribution, see the Wolfram MathWorld article Gamma Distribution.
Example
// compile with: /EHsc /W4 #include #include #include #include #include void test(const double a, const double b, const int s) < // uncomment to use a non-deterministic generator // std::random_device gen; std::mt19937 gen(1701); std::gamma_distribution<>distr(a, b); std::cout histogram; for (int i = 0; i < s; ++i) < ++histogram[distr(gen)]; >// print results std::cout std::cout int main() < double a_dist = 0.0; double b_dist = 1; int samples = 10; std::cout > a_dist; std::cout > b_dist; std::cout > samples; test(a_dist, b_dist, samples); > Use CTRL-Z to bypass data entry and run using default values. Enter a floating point value for the 'alpha' distribution parameter (must be greater than zero): 1 Enter a floating point value for the 'beta' distribution parameter (must be greater than zero): 1 Enter an integer value for the sample count: 10 min() == 4.94066e-324 max() == 1.79769e+308 alpha() == 1.0000000000 beta() == 1.0000000000 Distribution for 10 samples: 1: 0.0936880533 2: 0.1225944894 3: 0.6443593183 4: 0.6551171649 5: 0.7313457551 6: 0.7313557977 7: 0.7590097389 8: 1.4466885214 9: 1.6434088411 10: 2.1201210996 Requirements
Namespace: std
gamma_distribution::gamma_distribution
Constructs the distribution.
explicit gamma_distribution(result_type alpha = 1.0, result_type beta = 1.0); explicit gamma_distribution(const param_type& parm); Parameters
alpha
The alpha distribution parameter.
beta
The beta distribution parameter.
parm
The parameter structure used to construct the distribution.
Remarks
Precondition: 0.0 < alpha and 0.0 < beta
The first constructor constructs an object whose stored alpha value holds the value alpha and whose stored beta value holds the value beta.
The second constructor constructs an object whose stored parameters are initialized from parm. You can obtain and set the current parameters of an existing distribution by calling the param() member function.
gamma_distribution::param_type
Stores the parameters of the distribution.
struct param_type < typedef gamma_distributiondistribution_type; param_type(result_type alpha = 1.0, result_type beta 1.0); result_type alpha() const; result_type beta() const; bool operator==(const param_type& right) const; bool operator!=(const param_type& right) const; >; Parameters
alpha
The alpha distribution parameter.
beta
The beta distribution parameter.
right
The param_type instance to compare this to.
Remarks
Precondition: 0.0 < alpha and 0.0 < beta
This structure can be passed to the distribution’s class constructor at instantiation, to the param() member function to set the stored parameters of an existing distribution, and to operator() to be used in place of the stored parameters.
std:: tgamma, std:: tgammaf, std:: tgammal
If no errors occur, the value of the gamma function of num , that is \(\Gamma(\mathtt) = \displaystyle\int_0^\infty\!\! t^<\mathtt-1> e^\, dt\) ∫ ∞
0 t num-1
e -t dt , is returned.
If a domain error occurs, an implementation-defined value (NaN where supported) is returned.
If a pole error occurs, ±HUGE_VAL , ±HUGE_VALF , or ±HUGE_VALL is returned.
If a range error due to overflow occurs, ±HUGE_VAL , ±HUGE_VALF , or ±HUGE_VALL is returned.
If a range error due to underflow occurs, the correct value (after rounding) is returned.
[edit] Error handling
Errors are reported as specified in math_errhandling .
If num is zero or is an integer less than zero, a pole error or a domain error may occur.
If the implementation supports IEEE floating-point arithmetic (IEC 60559),
- If the argument is ±0, ±∞ is returned and FE_DIVBYZERO is raised
- If the argument is a negative integer, NaN is returned and FE_INVALID is raised
- If the argument is -∞, NaN is returned and FE_INVALID is raised
- If the argument is +∞, +∞ is returned
- If the argument is NaN, NaN is returned
[edit] Notes
If num is a natural number, std :: tgamma ( num ) is the factorial of num — 1 . Many implementations calculate the exact integer-domain factorial if the argument is a sufficiently small integer.
For IEEE-compatible type double , overflow happens if 0 < num && num < 1 / DBL_MAX or if num > 171.7 .
POSIX requires that a pole error occurs if the argument is zero, but a domain error occurs when the argument is a negative integer. It also specifies that in future, domain errors may be replaced by pole errors for negative integer arguments (in which case the return value in those cases would change from NaN to ±∞).
There is a non-standard function named gamma in various implementations, but its definition is inconsistent. For example, glibc and 4.2BSD version of gamma executes lgamma , but 4.4BSD version of gamma executes tgamma .
The additional overloads are not required to be provided exactly as (A) . They only need to be sufficient to ensure that for their argument num of integer type, std :: tgamma ( num ) has the same effect as std :: tgamma ( static_cast < double >( num ) ) .
[edit] Example
#include #include #include #include #include // #pragma STDC FENV_ACCESS ON int main() { std::cout "tgamma(10) = " std::tgamma(10) ", 9! = " 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 '\n' "tgamma(0.5) = " std::tgamma(0.5) ", sqrt(pi) = " std::sqrt(std::acos(-1)) '\n'; // special values std::cout "tgamma(1) = " std::tgamma(1) '\n' "tgamma(+Inf) = " std::tgamma(INFINITY) '\n'; // error handling errno = 0; std::feclearexcept(FE_ALL_EXCEPT); std::cout "tgamma(-1) = " std::tgamma(-1) '\n'; if (errno == EDOM) std::cout " errno == EDOM: " std::strerror(errno) '\n'; if (std::fetestexcept(FE_INVALID)) std::cout " FE_INVALID raised\n"; } tgamma(10) = 362880, 9! = 362880 tgamma(0.5) = 1.77245, sqrt(pi) = 1.77245 tgamma(1) = 1 tgamma(+Inf) = inf tgamma(-1) = nan errno == EDOM: Numerical argument out of domain FE_INVALID raised