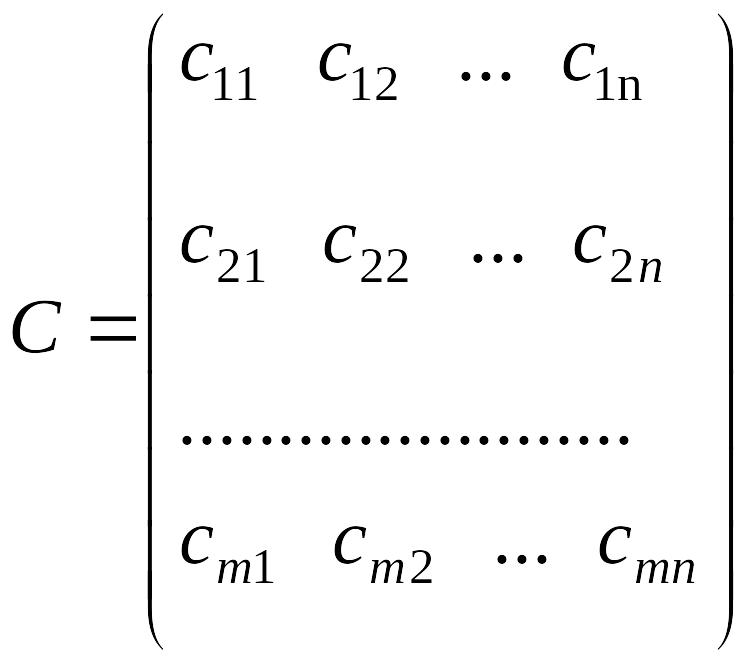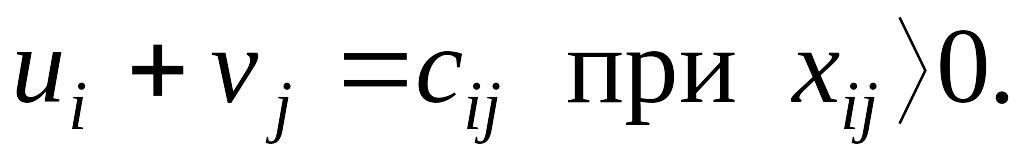5. Транспортная задача линейного программирования
Под названием «транспортная задача» объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
5.1. Формулировка транспортной задачи
Однородный груз сосредоточен у т поставщиков в объемах a1, a2,. ат. Данный груз необходимо доставить п потребителям в объемах b1, b2, . bn. Известны сij, i= 1, 2, . m, j = 1, 2, . п — стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков будут вывезены полностью, запросы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны.
Исходные данные транспортной задачи обычно записываются в таблице:
Исходные данные задачи могут быть представлены также в виде вектора запасов поставщиков А=(a1,a2,. ат), вектора запросов потребителей В=(b1,b2, . bn) и матрицы стоимостей
5.2. Алгоритм решения транспортной задачи методом потенциалов
Порядок решения транспортных задач методом потенциалов.
- Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивного поставщика или потребителя с недостающими запасами или запросами и нулевыми стоимостями перевозок.
- Строят начальное опорное решение и проверяют правильность его построения, для чего подсчитывают количество занятых клеток (их должно быть т+п—1) и убеждаются в линейной независимости векторов-условий.
3.Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений Для того чтобы найти частное решение системы, одному из потенциалов задают произвольно некоторое значение (чаще нуль). Остальные потенциалы однозначно определяются по формулам:
при если известен потенциал , и
при если известен потенциал .
4. Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам и те оценки, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток < 0, то вычисляют значение целевой функции, и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным.
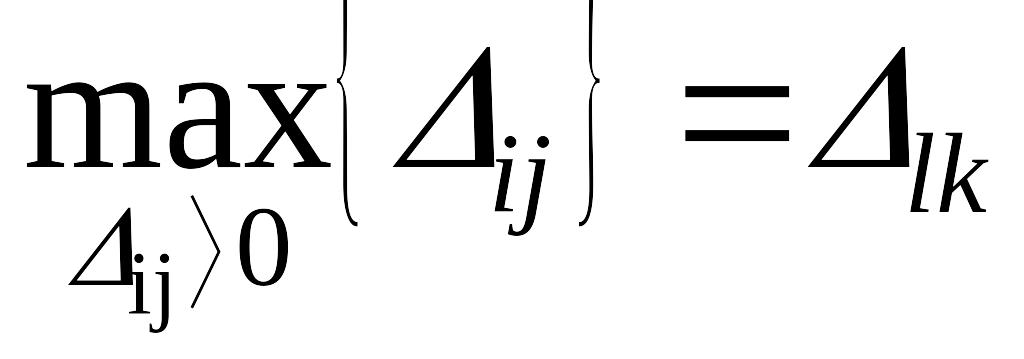
5. Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка . Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину θ= . Клетка со знаком «-», в которой достигается , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным т+ п—1. Возвращаются к пункту 3.
Пример. Решить транспортную задачу, данные приведены в таблице