Find number of divisors python

How to find all the possible proper divisor of an integer in Python3

In this tutorial, we will learn how to find all the possible divisors of an integer in Python. This problem uses a very basic mathematical concept and basic python.

By the time you will be done reading this post, you will be through with both of the concepts and will easily learn to code the concept as well.

Find DIVISORS of an integer in Python

This problem is based on simple mathematical division. Let us begin :
If a number divides the given number completely leaving the remainder to be 0(zero) then it is said to be the positive proper divisor of that integer(excluding that number) and if we include the number too then we will get all the divisors of the number.

Example: 1,2,4 are positive proper divisors of 8 and if we include 8 then we will get all the divisors of 8.

Divisors of an integer in Python

We will first take user input (say N) of the number we want to find divisors. Then we will run a loop from 1 to (N+1). We do so because if we run the loop from 0(zero) then we will get ‘Division By Zero Error’. And if we run it only N times then we will not get the number(N) as its own divisor. Within the loop, we will check the dividing condition. If the remainder after dividing N with X( X is from 1 to N) is 0 then we will print X. When the loop will be over, we will get the answer.

N=(int)(input("Enter Number: ")) for x in range(1,N+1): if(N%x==0): print(x)

INPUT: Enter Number: 5 OUTPUT: 1 5

Источник

Find number of divisors python

Как найти все делители числа в Python

При работе с числами в Python часто требуется находить все делители заданного числа. Нахождение всех делителей может быть полезно для решения различных задач, таких как нахождение наибольшего общего делителя, проверка числа на простоту и т.д. В этой статье мы рассмотрим несколько способов нахождения всех делителей числа в Python.

Простой подход нахождения делителей

Простой подход заключается в переборе всех чисел от 1 до заданного числа n и проверке каждого числа на деление на n . Код для нахождения всех делителей числа n с помощью наивного подхода будет выглядеть следующим образом:

def find_divisors(n):  divisors = []  for i in range(1, n+1):  if n % i == 0:  divisors.append(i)  return divisors 

Этот код работает корректно и находит все делители заданного числа. Однако, его сложность времени составляет O(n), что может быть неприемлемо для больших чисел.

Более оптимальный подход нахождения делителей

Второй способ нахождения всех делителей заключается в переборе только чисел от 1 до корня из заданного числа n. Если мы нашли делитель i , то мы также можем добавить в список делителей n/i . Код для нахождения всех делителей числа n с помощью более оптимального подхода будет выглядеть следующим образом:

import math def find_divisors(n):  divisors = []  for i in range(1, int(math.sqrt(n))+1):  if n % i == 0:  divisors.append(i)  if i != n // i:  divisors.append(n // i)  return divisors 

Этот код работает корректно и имеет сложность времени O(sqrt(n)) , что гораздо лучше, чем простой подход.

Решето Эратосфена в Python

Третий способ нахождения всех делителей заключается в нахождении всех простых делителей заданного числа и их степеней. Для нахождения простых делителей мы можем использовать Решето Эратосфена.

Затем мы будем проверять, на какие степени делятся каждый из простых делителей. Код для нахождения всех делителей числа n с помощью Решета Эратосфена будет выглядеть следующим образом:

def sieve_of_eratosthenes(n):  primes = [True for i in range(n+1)]  p = 2  while p**2  n:  if primes[p]:  for i in range(p**2, n+1, p):  primes[i] = False  p += 1  return [i for i in range(2, n+1) if primes[i]]  def prime_factors(n):  factors = []  primes = sieve_of_eratosthenes(n)  for p in primes:  while n % p == 0:  factors.append(p)  n //= p if n > 1:  factors.append(n)  return factors 

Эти функции могут быть использованы для нахождения делителей любого целого числа. Например, для числа 12 результат работы этих функций будет таким:

>>> find_divisors(12) [1, 2, 3, 4, 6, 12]  >>> prime_factors(12) [2, 2, 3] 

Источник

How to Get All Divisors of a Number in Python?

Get all divisors c of the number n so that c * i = n for another integer i . The desired output format is a list of integers (divisors).

Here are a couple of examples:

n = 10 # Output: [1, 2, 5, 10] n = 13 # Output: [1, 13] n = 24 # Output: [1, 2, 3, 4, 6, 8, 12]

Method 1: Naive Approach

Integer i is a divisor of n if n modulo i is zero.

We use this observation in the function divisors() . We create an initially empty list result and check for every integer number i between 0 and n/2 whether this number is a divisor of n . If it is, we append it to the list.

The following Python code accomplishes this:

def divisors(n): result = [] for i in range(1, n//2 + 1): if n % i == 0: result.append(i) result.append(n) return result print(divisors(24)) # [1, 2, 3, 4, 6, 8, 12, 24]

This approach is not very efficient because we traverse every single number from 0 to n/2 . If the number n becomes large such as n=1000000 , we need to check every number i=0, i=1, i=2, i=3, . i=500000 .

Runtime complexity: The runtime complexity of calculating the divisors of number n is O(n) using this approach assuming the modulo operation can be performed in one step.

Method 2: Reducing the Number of Loop Iterations

We use two observations to reduce the number of loop iterations of the “naive algorithm”.

Observation 1: If number i is a divisor of n , number j = n/i must be an integer and a divisor of n as well because i * n/i = n . This means that each time we find a divisor i , we can also add the divisor n/i to the list of divisors.

Observation 2: For a pair of n -divisors (i, j) , one of them must be smaller than or equal to the square root of n . The reason is simple: if both were larger than the square root, the multiplication i * j would be larger than n for sure because root(n) * root(n) == n . Thus, we can traverse the potential divisors from i=0 to i=root(n) and be sure to have found all divisors. This saves us all iterations from i=root(n) to i=n//2 .

Here’s the simple tweak with significant performance benefits:

def divisors(n): result = set() for i in range(1, int(n**0.5)+1): if n % i == 0: result.add(i) result.add(n//i) return list(result) print(divisors(24)) # [1, 2, 3, 4, 6, 8, 12, 24]

This code iterates only from 0 to the square root of the number n . If we find a divisor i , we also add n//i which is the other factor and a divisor of n as well.

Runtime complexity: The runtime complexity of calculating the divisors of number n is O(n^0.5) using this approach assuming the modulo operation is counted as one step.

Programmer Humor – Blockchain

Where to Go From Here?

Enough theory. Let’s get some practice!

Coders get paid six figures and more because they can solve problems more effectively using machine intelligence and automation.

To become more successful in coding, solve more real problems for real people. That’s how you polish the skills you really need in practice. After all, what’s the use of learning theory that nobody ever needs?

You build high-value coding skills by working on practical coding projects!

Do you want to stop learning with toy projects and focus on practical code projects that earn you money and solve real problems for people?

🚀 If your answer is YES!, consider becoming a Python freelance developer! It’s the best way of approaching the task of improving your Python skills—even if you are a complete beginner.

If you just want to learn about the freelancing opportunity, feel free to watch my free webinar “How to Build Your High-Income Skill Python” and learn how I grew my coding business online and how you can, too—from the comfort of your own home.

While working as a researcher in distributed systems, Dr. Christian Mayer found his love for teaching computer science students.

To help students reach higher levels of Python success, he founded the programming education website Finxter.com that has taught exponential skills to millions of coders worldwide. He’s the author of the best-selling programming books Python One-Liners (NoStarch 2020), The Art of Clean Code (NoStarch 2022), and The Book of Dash (NoStarch 2022). Chris also coauthored the Coffee Break Python series of self-published books. He’s a computer science enthusiast, freelancer, and owner of one of the top 10 largest Python blogs worldwide.

His passions are writing, reading, and coding. But his greatest passion is to serve aspiring coders through Finxter and help them to boost their skills. You can join his free email academy here.

Be on the Right Side of Change 🚀

• The world is changing exponentially. Disruptive technologies such as AI, crypto, and automation eliminate entire industries. 🤖
• Do you feel uncertain and afraid of being replaced by machines, leaving you without money, purpose, or value? Fear not! There a way to not merely survive but thrive in this new world!
• Finxter is here to help you stay ahead of the curve, so you can keep winning as paradigms shift.

Learning Resources 🧑‍💻

⭐ Boost your skills. Join our free email academy with daily emails teaching exponential with 1000+ tutorials on AI, data science, Python, freelancing, and Blockchain development!

Join the Finxter Academy and unlock access to premium courses 👑 to certify your skills in exponential technologies and programming.

New Finxter Tutorials:

Finxter Categories:

Источник

Python: Find the number of divisors of a given integer is even or odd

Write a Python program to find the total number of even or odd divisors of a given integer.

Sample Solution:

Python Code:

def divisor(n): x = len([i for i in range(1,n+1) if not n % i]) return x print(divisor(15)) print(divisor(12)) print(divisor(9)) print(divisor(6)) print(divisor(3)) 

Pictorial Presentation:

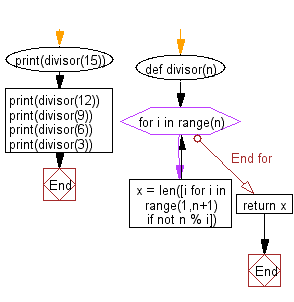
Visualize Python code execution:

The following tool visualize what the computer is doing step-by-step as it executes the said program:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

What is the difficulty level of this exercise?

Test your Programming skills with w3resource’s quiz.

Follow us on Facebook and Twitter for latest update.

Python: Tips of the Day

Find current directory and file’s directory:

To get the full path to the directory a Python file is contained in, write this in that file:

import os dir_path = os.path.dirname(os.path.realpath(__file__))

(Note that the incantation above won’t work if you’ve already used os.chdir() to change your current working directory, since the value of the __file__ constant is relative to the current working directory and is not changed by an os.chdir() call.)

To get the current working directory use

Documentation references for the modules, constants and functions used above:

• The os and os.path modules.
• The __file__ constant
• os.path.realpath(path) (returns «the canonical path of the specified filename, eliminating any symbolic links encountered in the path»)
• os.path.dirname(path) (returns «the directory name of pathname path»)
• os.getcwd() (returns «a string representing the current working directory»)
• os.chdir(path) («change the current working directory to path»)

• Weekly Trends
• Java Basic Programming Exercises
• SQL Subqueries
• Adventureworks Database Exercises
• C# Sharp Basic Exercises
• SQL COUNT() with distinct
• JavaScript String Exercises
• JavaScript HTML Form Validation
• Java Collection Exercises
• SQL COUNT() function
• SQL Inner Join
• JavaScript functions Exercises
• Python Tutorial
• Python Array Exercises
• SQL Cross Join
• C# Sharp Array Exercises

We are closing our Disqus commenting system for some maintenanace issues. You may write to us at reach[at]yahoo[dot]com or visit us at Facebook

Источник