Exponential moving average in python

Python Trading Toolbox: Weighted and Exponential Moving Averages

In the first post of the Financial Trading Toolbox series (Building a Financial Trading Toolbox in Python: Simple Moving Average), we discussed how to calculate a simple moving average, add it to a price series chart, and use it for investment and trading decisions. The Simple Moving Average is only one of several moving averages available that can be applied to price series to build trading systems or investment decision frameworks. Among those, two other moving averages are commonly used among financial market :

• Weighted Moving Average (WMA)
• Exponential Moving Average (EMA)

In this article, we will explore how to calculate those two averages and how to ensure that the results match the definitions that we need to implement.

Weighted Moving Average

In some applications, one of the limitations of the simple moving average is that it gives equal weight to each of the daily prices included in the window. E.g., in a 10-day moving average, the most recent day receives the same weight as the first day in the window: each price receives a 10% weighting.

Compared to the Simple Moving Average, the Linearly Weighted Moving Average (or simply Weighted Moving Average, WMA), gives more weight to the most recent price and gradually less as we look back in time. On a 10-day weighted average, the price of the 10th day would be multiplied by 10, that of the 9th day by 9, the 8th day by 8 and so on. The total will then be divided by the sum of the weights (in this case: 55). In this specific example, the most recent price receives about 18.2% of the total weight, the second more recent 16.4%, and so on until the oldest price in the window that receives 0.02% of the weight.

Let’s put that in practice with an example in Python. In addition to pandas and Matplotlib, we are going to make use of NumPy:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl

We apply a style for our charts. If you’re using Jupyter it’s a good idea to add the %matplotlib inline instruction (and skip plt.show() when creating charts):

Источник

Theory

The exponential moving average differs from the simple moving average in that more recent samples are more strongly weighted. This means that the exponential moving average responds more quickly to changes in the signal.

Implementation

The signal parameter is a one dimensional array. the smoothing parameter controls how much influence the more recent samples have on the value of the average.

import numpy as np def exponential_moving_average(signal, points, smoothing=2): """ Calculate the N-point exponential moving average of a signal Inputs: signal: numpy array - A sequence of price points in time points: int - The size of the moving average smoothing: float - The smoothing factor Outputs: ma: numpy array - The moving average at each point in the signal """ weight = smoothing / (points + 1) ema = np.zeros(len(signal)) ema[0] = signal[0] for i in range(1, len(signal)): ema[i] = (signal[i] * weight) + (ema[i - 1] * (1 - weight)) return ema 

Results

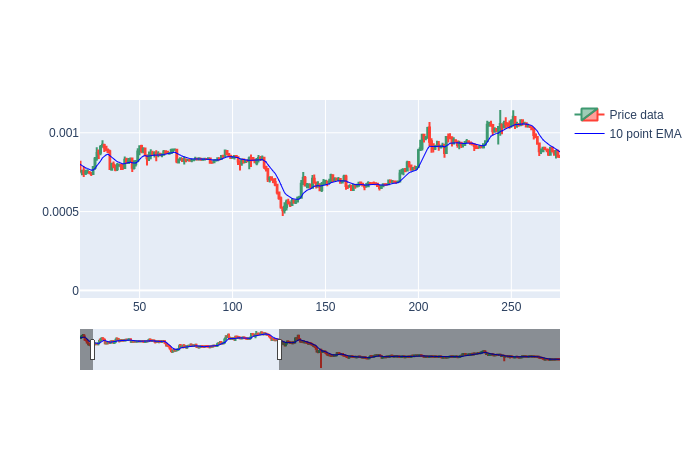
Consider the following diagram showing the exponential average in blue and the simple average in red. Note that the exponential average leads the simple average, reacting to price changes more quickly.

Источник

Moving averages with Python

Simple, cumulative, and exponential moving averages with Pandas

The moving average is commonly used with time series to smooth random short-term variations and to highlight other components (trend, season, or cycle) present in your data. The moving average is also known as rolling mean and is calculated by averaging data of the time series within k periods of time. Moving averages are widely used in finance to determine trends in the market and in environmental engineering to evaluate standards for environmental quality such as the concentration of pollutants.

In this article, we briefly explain the most popular types of moving averages: (1) the simple moving average (SMA), (2) the cumulative moving average (CMA), and (3) the exponential moving average (EMA). In addition, we show how to implement them with Python. To do so, we use two data sets from Open Data Barcelona, containing rainfall and temperatures of Barcelona from 1786 until 2019.

Data pre-processing

In this article, we are going to use two data sets available in Open Data Barcelona: (1) Monthly average air temperatures of the city of Barcelona since 1780, and (2) Monthly accumulated rainfall of the city of Barcelona since 1786. You can easily download them at the following links.

Источник

5. Accurately Compute Exponential Moving Averages in Pandas and Python

In our previous post, we have explained how to compute simple moving averages in Pandas and Python. In this post, we explain how to compute exponential moving averages in Pandas and Python. It should be noted that the exponential moving average is also known as an exponentially weighted moving average in finance, statistics, and signal processing communities. The codes that are explained in this post and in our previous posts can be found on the GitHub page. The video accompanying this post is given below.

Next, we explain how to easily compute the exponential moving averages using the built-in Pandas function ewm(). We also compare the results with the manually computed exponential moving averages. The code is given below.

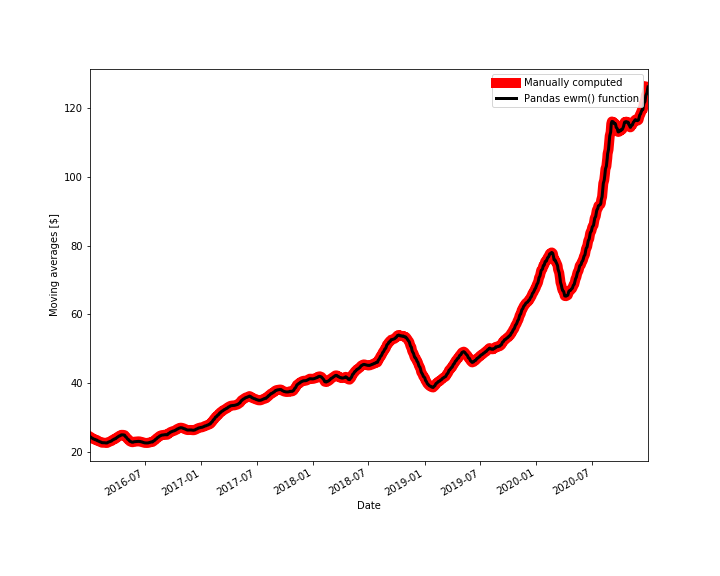
# now verify the results by using the Pandas function # https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.ewm.html exponential_moving_average_pandas=data['Adj Close'].ewm(span=time_period, adjust=False).mean() # explanation of the parameters # span : float, optional - Specify decay in terms of span, α=2/(span+1), for span≥1. #adjust: bool, default True # When adjust=False, the exponentially weighted function is calculated recursively: # y0=x0 # yt=(1−α)yt−1+αxt, # CONSEQUENTLY, the parameter "adjust" should be set to "False" #compare the results fig2=plt.figure(figsize=(10,8)) ax2=fig2.add_subplot(111,ylabel='Moving averages [$]') data['Exponential_moving_average'].plot(ax=ax2, color='r', lw=10, label='Manually computed', legend = True ) exponential_moving_average_pandas.plot(ax=ax2, color='k', lw=3, label='Pandas ewm() function', legend = True) plt.savefig('exponential_moving_average_comparison.png') plt.show()

This code block produces the following figure that compares the Pandas function ewm() with the manual method for computing the exponential moving averages.

Figure 2 shows that the two methods produce the identical results.

This is the end of this lecture. In this lecture we learned how to compute the exponential moving averages of stock prices using two methods.

Источник

Как рассчитать экспоненциальную скользящую среднюю в Pandas

В анализе временных рядов скользящая средняя — это просто среднее значение определенного количества предыдущих периодов.

Экспоненциальное скользящее среднее — это тип скользящего среднего, который придает больший вес недавним наблюдениям, что означает, что он может быстрее фиксировать последние тенденции.

В этом руководстве объясняется, как рассчитать экспоненциальное скользящее среднее для столбца значений в кадре данных pandas.

Пример: экспоненциальная скользящая средняя в Pandas

Предположим, у нас есть следующие Pandas DataFrame:

import pandas as pd #create DataFrame df = pd.DataFrame() #view DataFrame df period sales 0 1 25 1 2 20 2 3 14 3 4 16 4 5 27 5 6 20 6 7 12 7 8 15 8 9 14 9 10 19 

Мы можем использовать функцию pandas.DataFrame.ewm() для вычисления экспоненциально взвешенной скользящей средней за определенное количество предыдущих периодов.

Например, вот как рассчитать экспоненциально взвешенную скользящую среднюю, используя четыре предыдущих периода:

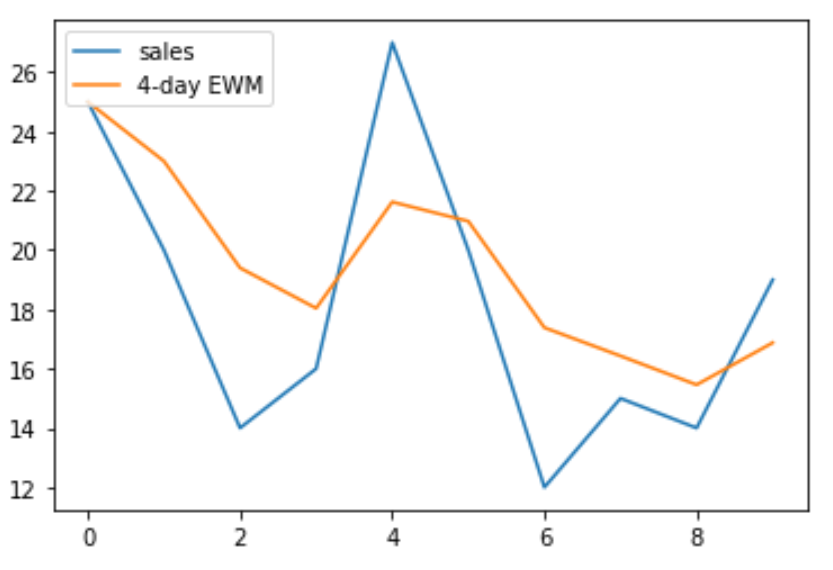
#create new column to hold 4-day exponentially weighted moving average df['4dayEWM'] = df['sales']. ewm (span= 4 , adjust= False ).mean() #view DataFrame df period sales 4dayEWM 0 1 25 25.000000 1 2 20 23.000000 2 3 14 19.400000 3 4 16 18.040000 4 5 27 21.624000 5 6 20 20.974400 6 7 12 17.384640 7 8 15 16.430784 8 9 14 15.458470 9 10 19 16.875082 

Мы также можем использовать библиотеку matplotlib для визуализации продаж по сравнению с 4-дневной экспоненциально взвешенной скользящей средней:

import matplotlib.pyplot as plt #plot sales and 4-day exponentially weighted moving average plt.plot(df['sales'], label='Sales') plt.plot(df['4dayEWM'], label='4-day EWM') #add legend to plot plt.legend(loc=2) 

Источник