Двухкритериальная задача линейного программирования

5 Вариант.

Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В.

а1= 19, а2= 16, а3= 19, b1= 31, b2= 9, b3= 1, c1= 1121, c2= 706, c3= 1066,

Задача 2. Фирме необходимо выбрать наилучший вариант закупки оборудования, если задана закупочная цена каждого из вариантов оборудования и время изготовления и доставки. Под наилучшим вариантом понимается вариант с минимальными закупочной стоимостью и временем доставки.

А) Для заданной двухкритериальной задачи, задавшись коэффициентами α и β провести линейную свертку критериев ии определить минимальное решение.

Б) Для заданной двухкритериальной задачи найти множество Парето в случае двух критериев вида и.

Значения изаданы таблицей:

Контрольные вопросы

1. Какие задачи называются однокритериальными?
2. Какие задачи называются многокритериальными?
3. Какие способы решения однокритериальных задач вы знаете?
4. Какие подходы к отысканию подходящего решения вы знаете у противоречивых критериев?
5. Какое множество называется множеством Парето?

Практическая работа №3 «Сведение произвольной задачи линейного программирования к озлп. Решение задач линейного программирования симплекс-методом»

Цель работы: Научиться сводить произвольную задачу линейного программирования к основной задаче линейного программирования. Решить задачу линейного программирования симплекс-методом.

Краткая теория

Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования. Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального). Общая форма задачи линейного программирования формулируют следующим образом:

	(1)
	(2)
	(3)

Коэффициенты a_i,j, b_i, c_j, j = 1, 2, . , n, i =1, 2, . , m– любые действительные числа (возможно 0). Итак, решения, удовлетворяющие системе ограничений (1) условий задачи и требованиям неотрицательности (2), называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) (3) целевой функции, —оптимальными. Выше описанная задача линейного программирования (ЗЛП) представлена в общей форме, но одна и та же (ЗЛП) может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная. В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, . х_n являются неотрицательными:

	(4)
	(5)
	(6)

К канонической форме можно преобразовать любую задачу линейного программирования. Правило приведения ЗЛП к каноническому виду: 1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» — со знаком «-»

(7)

Вводим переменную 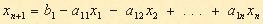. Тогда неравенство (7) запишется в виде:

(8)

В каждое из неравенств вводится своя “уравнивающая” переменная, после чего система ограничений становится системой уравнений. 2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных

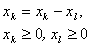, l — свободный индекс

3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1) 4. Наконец, если исходная задача была задачей на минимум, то введением новой целевой функции F₁ = -F мы преобразуем нашу задачу на минимум функции F в задачу на максимум функции F₁. Таким образом, всякую задачу линейного программирования можно сформулировать в канонической форме. В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа « = ». Все переменные задачи неотрицательны.

	(9)

Всякую задачу линейного программирования можно сформулировать в стандартной форме. Преобразование задачи на минимум в задачу на максимум, а также обеспечение не отрицательности переменных производится так же, как и раньше. Всякое равенство в системе ограничений равносильно системе взаимопротивоположных неравенств: 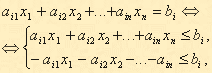Существует и другие способы преобразования системы равенств в систему неравенств, т.е. всякую задачу линейного программирования можно сформулировать в стандартной форме. Решение задач линейного программирования симплекс-методом. Идея симплекс-метода заключается в последовательном улучшении первоначального плана путем упорядоченного перехода от одного опорно­го плана к другому и завершается нахождением оптимального плана. Сим­плекс-методом решаются только канонические задачи линейного программирования. Решение канонической задачи симплекс-методом существенно облегчается применением так называемых симплексных таблиц. Всякую каноническую задачу можно записать условно в виде таблицы. Таблица заполняется следующим образом: первые т строк содержат в условной форме уравнения системы ограничений, разрешенные относительно базис­ных переменных. В последней строке записана целевая функция, эта строка называется F -строкой. В столбцах записаны свободные переменные и свободные члены. Условие оптимальности плана: если ЗЛП на максимум, то в F-строке не должно быть отрицательных элементов; если ЗЛП на минимум, то в F-строке не должно быть положительных элементов.

Источник

Многокритериальные задачи линейного программирования, решение методом последовательных уступок.

Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость, надежность и т. п.). Требуется найти точку области допустимых решений, которая минимизирует или максимизирует все эти критерии.

Определить переговорное множество, а затем решить данную задачу методом последовательных уступок (допустимые уступки по первым двум критериям принять равными Максимизировать функции (5.1.), (5.2.), (5.3.):

При выполнении условий системы (5.4.)

И неотрицательности переменных:

Требуется определить переговорное множество, а затем решить данную задачу методом последовательных уступок (допустимые уступки по первым двум критериям принять равными .

• Если критерии на min, их следует привести к max умножением на -1;
• Критерии следует ранжировать по степени важности для предприятия;
• Назначаются уступки (величина допустимого отклонения .

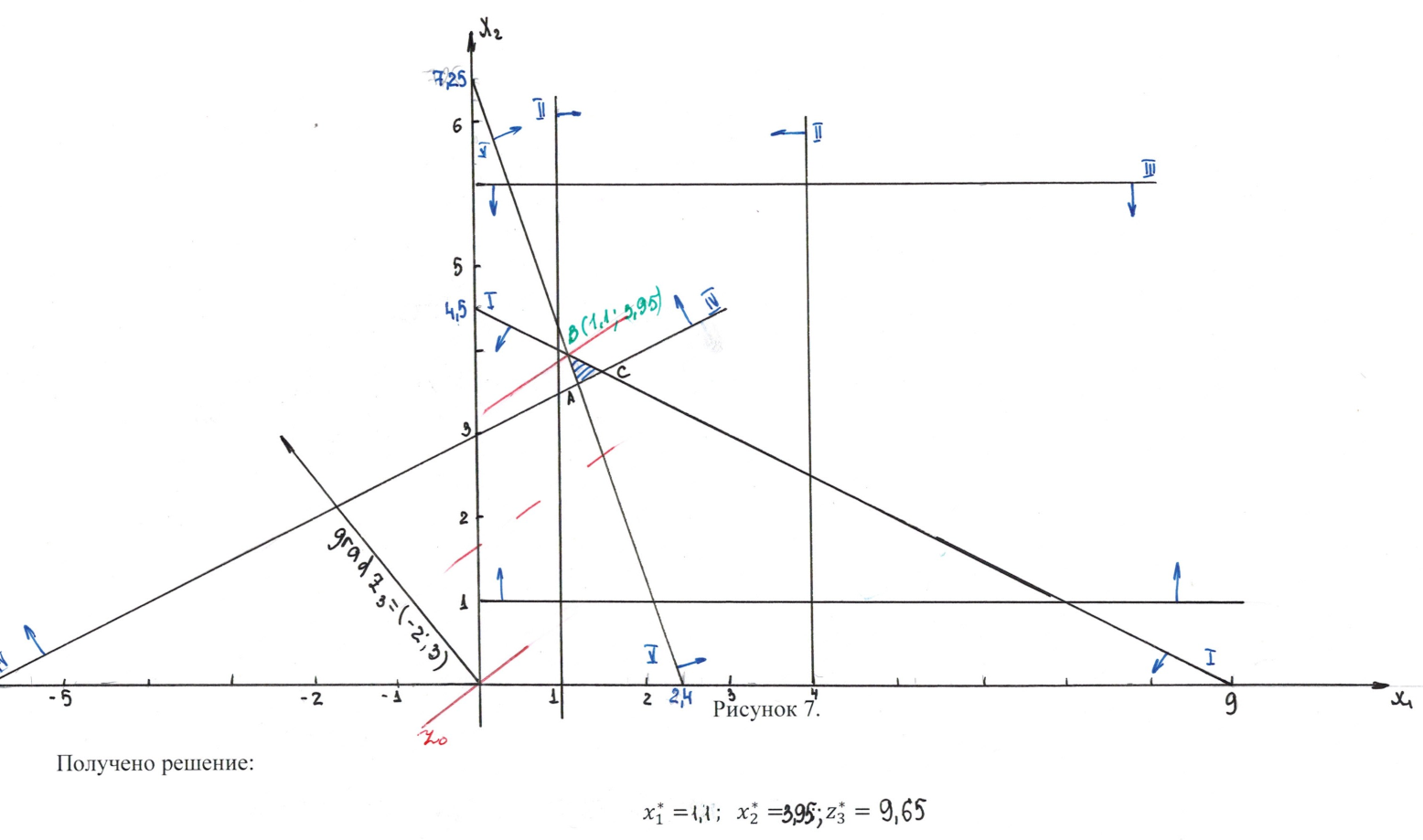
Для данной задачи переговорное множество совпадает с областью допустимых значений, построенной по системе (5.4). Максимизируем функцию при условиях (5.4.). Для этого удобно воспользоваться графическим методом (рисунок 5)

Переходим к максимизации функции при условиях (8.4) и дополнительном ограничении, учитывающем, что по критерию нельзя уступать более чем на . Так как , то дополнительное ограничение будет иметь вид: 6 (5.6.)

Графическое решение задач (5.2.), (5.4.), (5.5.) представлено на рисунке 6.

Переходим к максимизации функции при условиях (5.4) и дополнительном ограничении, учитывающем, что по критерию нельзя уступать более чем на . Так как 7,25 , то дополнительное ограничение будет иметь вид: (5.7.)

Графическое решение задач (5.2.), (5.4.), (5.5.) и (5.7.) представлено на рисунке (7).

Получено оптимальное решение многокритериальной задачи:

Векторы, действия над ними, линейная зависимость и независимость векторов, их линейная комбинация, базис.

Совокупность n чисел , заданных в определенном порядке, называется n-мерным вектором. Числа – компоненты (координаты) вектора. Число n – размерность вектора.

Два n-мерных вектора a и b называются равными, если все их соответствующие компоненты равны:

Сумма двух n-мерных векторов и есть вектор

Компоненты которого получаются сложением соответствующих компонентов данных векторов.

Операция сложения векторов обладает свойствами коммутативности и ассоциативности:

Вектор 0(0, 0, …, 0), все компоненты которого равны нулю, называется нуль-вектором. Каков бы ни был вектор а, справедливо равенство а+0=а, т.е. нуль-вектор ведет себя при сложении аналогично числу ноль при арифметике.

Вектор — противоположный вектору а. обозначается –а. очевидно, что а+(-а) = 0.

Операция вычитания определяется как сложение с противоположным вектором: a – b = a + (-b)

Произведение вектора на число λ – вектор , компоненты которого получаются умножением всех компонентов данного вектора на данное число. Такой вектор обозначается λа.

Операция умножения вектора на число обладает сочетательным свойством:

и распределительным свойством относительно векторного и числового сомножителей:

при умножении любого вектора на единицу этот вектор не изменится: 1а = а, а при умножении любого вектора на число нуль и любого числа на нуль вектор получается нуль-вектор:

Скалярное произведение двух n-мерных векторов а и b – число, равное сумме произведений одноименных координат данных векторов:

Операция скалярного умножения обладает следующими свойствами:

система векторов – упорядоченный набор векторов n-мерного пространства: S:

Линейная комбинация векторов системы S с коэффициентами , :

Если коэффициенты равны нулю, то такая линейная комбинация называется тривиальной.

Если существует ненулевое решение, то система называется линейно-зависимой. Если существует только тривиальное решение системы (1), то система линейно-независима.

Если какой-либо вектор системы линейно выражается через остальные вектора данной системы, то система является линейно-зависимой.

Если система содержит хотя бы один нулевой вектор, то такая система линейно-зависима.

Если количество векторов в системе больше размерности пространства, то система линейно-зависима. (размерность больше числа векторов  есть свободные переменные  система совместна).

Подсистема данной системы называется подсистемой образующих, если каждый вектор данной системы можно представить в виде линейной комбинации векторов подсистемы.

Базис системы векторов – всякая линейно-зависимая подсистема образующих.

Ранг системы векторов – количество базисных векторов в системе.

Источник