Двухиндексные задачи линейного программирования стандартная транспортная задача

2. Двухиндексные задачи линейного программирования. Стандартная транспортная задача (тз).

Задача о размещении (транспортная задача) – это распределительная задача (РЗ), в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.

Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Исходные параметры модели тз

1. m – количество пунктов отправления, n – количество пунктов назначения.
2. a_i – запас продукции в пункте отправления A_i (i =1,m) [ед. тов.].
3. b_j – спрос на продукцию в пункте назначения B_j ( j =1,n) [ед. тов.].
4. c_ij – тариф (стоимость) перевозки единицы продукции из пункта отправления A_i в пункт назначения B_j [руб./ед. тов.].

Целевая функция представляет собой транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте.

Составим таблицу затрат (табл. 1.1) таким образом, чтобы в ней фигурировали все издержки по перевозке единицы про­дукции от поставщика Аi к потребителю B_j. Эту таблицу назы­вают матрицей транспортных расходов:

По аналогии составляем матрицу неизвестных, где х_ij — это количество единиц продукции, доставляемой постав­щиком Ai потребителю Bj (табл. 2).

Объединим обе матрицы, поместив данные матрицы транс­портных расходов в верхнем правом углу каждой клетки, а не­известные— в центре каждой клетки (табл. 1.3).

Такую таблицу обычно называют матрицей (или планом) перевозок, а числа x_ij— перевозками.

К табл. 1.3 добавим снизу еще одну строку, где запишем числа, характеризующие потребность каждого потребителя, а справа—еще одни столбец, в котором будем указывать нали­чие продукции у поставщиков. В результате имеем новую таблицу (табл. 1.4), которая включает все условия и все неизвестные задачи. В клетке, расположенной на пересече­нии последней строки с последним столбцом и разделенной по диагонали, определим наличие баланса. Для этого подсчитаем наличие продукции у поставщиков, которая будет равна сумме всех данных последнего столбца, и потребность в этой продук­ции потребителей, равную сумме всех данных последней строки. Если обе суммы окажутся равными, то уравнение ба­ланса выполняется и задача разрешима.

Количество единиц продукции в пунктах назначения

Количество единиц продукции в пунктах потребления

Построение первого опорного плана.

Исходная таблица (табл. 1.5) до ее заполне­ния должна иметь такой же вид, что и таблица условий (см. табл. 1.4); свободными в ней должны быть середины клеток.

Количество единиц продукции в пунктах назначения

Количество единиц продукции в пунктах потребления

1. Всякое неотрицательное решение системы линейных уравнений, определяемое матрицей Х=(х_ij) называется допустимым планом транспортной задачи.
2. Ранг матрицы, составленный из коэффициентов при неизвестных системы линейных уравнений транспортной задачи, на единицу меньше числа уравнений, т.е. равен (m+n-1). Следовательно, число линейно независимых уравнений равно (m+n-1), они образуют базис, а соответствующие им (m+n-1) переменные будут являться базисными.
3. Допустимый план базисной задачи, имеющий не более (m+n-1) отличных от нуля величин х_ij называется опорным.
4. Если в опорном плане число отличных от нуля компонент равно в точности (m+n-1), то план является невырожденным, если меньше, то план называется вырожденным.
5. План Х=(х_ij), при котором функция (1.4) принимает свое минимальное значение, называется оптимальным планом ТЗ.
6. Для решения ТЗ необходимо и достаточно, чтобы суммарные запасы груза в пунктах отправления были равны сумме заявок пунктов назначения:

1. Модель ТЗ, удовлетворяющая условию (1.6), называется закрытой. Если указанное условие не выполняется, то модель называется открытой.

В случае превышения запаса над заявками

Вводится фиктивный (n+1) пункт назначения с потребностью

При вводится фиктивный (m+1) пункт отправления с запасом груза и соответствующие тарифы принимаются равными нулю: с_m+1,j=0, .

1. Наилучшим элементом матрицы тарифов С называется наименьший тариф, если задача поставлена на минимум, наибольший тариф — если задача поставлена на максимум целевой функции.

1. При построении исходного опорного плана задачи (или, как его еще называют, первоначальной матрицы перевозок) исполь­зуют различные методы, например метод северо-западного угла, который состоит в заполне­нии табл. 5 в направлении от левого верхнего угла к пра­вому нижнему.

Если модель ТЗ открытая и введены фиктивный поставщик или потребитель, то распределение осуществляется сначала для действительных поставщиков и потребителей и в последнюю очередь нераспределенный груз направляется от фиктивного поставщика или к фиктивному потребителю.

1. Дальнейшее улучшение первого опорного плана и получение оптимального плана производим методом потенциалов, который основан на теории двойственности

План Х=(х_ij) ТЗ будет являться оптимальным, если существует система m+n чисел _i, _j называемых потенциалами, удовлетворяющая условиям:

Потенциалы означают оплату за перевозку единицы груза в пунктах отправления и назначения соответственно, поэтому их сумма равна транспортному тарифу _i+_j=c_ij.

Введем обозначение оценки свободной клетки таблицы

Если среди оценок _ij нет положительных (задача поставлена на минимум), то опорный план считается оптимальным.

Алгоритм оценки оптимальности плана методом потенциалов включает следующие этапы:

1. Построение первого опорного плана;
2. Проверка вырожденности плана. Потенциалы могут быть только рассчитаны для невырожденного плана. Если число занятых клеток в опорном плане меньше, чем (m+n-1), то не хватит количества уравнений для определения потенциалов , поэтому вносим нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным (m+n-1). Нуль вводят в клетку с наименьшим тарифом, например в клетку одновременно вычеркиваемых строки и столбца таблицы при составлении нового плана. При этом фиктивно занятая нулем клетка не должна образовывать замкнутого прямоугольного контура с другими клетками таблицы.
3. Определение значения функции цели .
4. Проверка условия оптимальности. Определяем потенциалы. Для каждой занятой клетки таблицы записываем уравнение _i+_j=c_ij. Получим систему (m+n-1) уравнений с (m+n) переменными. Так как число переменных больше числа уравнений (m+n>m+n-1), то система является неопределенной и имеет бесконечное множество решений. Поэтому одному из неизвестных потенциалов задают произвольное значение, например, ₁=0. В транспортную таблицу добавляются дополнительная строка и столбец, куда заносятся потенциалы.

Определяем оценки свободных клеток _ij.

1. Построение нового плана. Из всех положительных оценок свободных клеток выбираем наибольшую если (задача поставлена на минимум), из отрицательных – наибольшую по абсолютной величине (задача поставлена на максимум). Клетку, которой соответствует наибольшая оценка, следует наполнить. Заполняя выбранную клетку необходимо изменить объемы поставок, записанных в ряде других занятых и связанных с заполняемой т.н. циклом.

Циклом пересчета матрицы называют замкнутую ломаную линию, обладающую следующими свойствами:

• вершины ломаной лежат в центрах клеток матрицы, при­чем только одна вершина расположена в свободной клетке, а остальные в базисных;
• звенья ломаной располагаются параллельно либо стро­кам, либо столбцам матрицы;
• в каждой вершине пересекаются только два звена;
• никакие три вершины не лежат на одной прямой;
• вершина, лежащая в свободной клетке матрицы, счита­ется положительной, и около нее ставится знак «+»;
• все остальные вершины получают знак « + » или «—» с таким расчетом, чтобы любые две соседние вершины имели разные знаки.

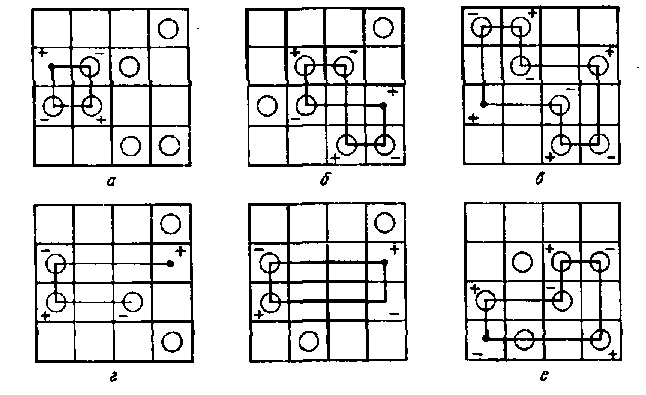
Например, если базисные клетки матрицы отметить круж­ками, а остальные оставить свободными, то ломаные линии, изображенные на рис. 1,а-в, являются циклами пересчета, так как удовлетворяют всем шести перечисленным выше усло­виям.

Ломаная, изображенная на рис. 1, г, не является циклом пересчета, так как она не замкнута.

На рис. 1, д изображена другая ломаная, которая тоже не может быть циклом пересчета, так как две вершины ее рас­положены в свободных клетках. Наконец, не является циклом пересчета и ломаная, показанная на рис. 1, е (ее вершина, расположенная в свободной клетке, имеет знак «-»).

Доказано, что для любой свободной клетки матрицы перевозок можно составить цикл пересчета, причем для невырож­денного плана перевозок он единственный.

Сдвигом по циклу пересчета на число х назовем операцию, суть которой состоит в том, что во всех положительных верши­нах цикла к числам добавляют число (+х), а к отрицатель­ным (-х).

Из объемов груза, стоящих в минусовых клетках, выбираем наименьшее – х. В свободную вершину цикла запишем число х, на которое осуществляем сдвиг; выберем направление пересчета, например по часовой стрелке от свободной вершины цикла; двигаясь вдоль вершин цикла в указанном направлении, прибавляем поочередно к числам, расположенным в положи­тельных вершинах, (+х), а к числам, расположенным в отри­цательных вершинах цикла, (-х).

В результате получается другая матрица. Полученный новый план проверяем на оптимальность, т.е. возвращаемся к четвертому этапу алгоритма.

Если в минусовых клетках построенного цикла находятся два (или несколько) одинаковых минимальных значения х_ij, то при распределении груза план становится вырожденным. Для продолжения решения необходимо одну или несколько освобождающихся клеток таблицы занять нулем причем предпочтение отдается клетке с наименьшим тарифом. Нулей вводится столько, чтобы во вновь полученном плане число занятых клеток было равно (m+n-1).

Значение целевой функции на каждой итерации можно рассчитать следующим образом:

(задача поставлена на минимум);

(задача поставлена на максимум).

Источник