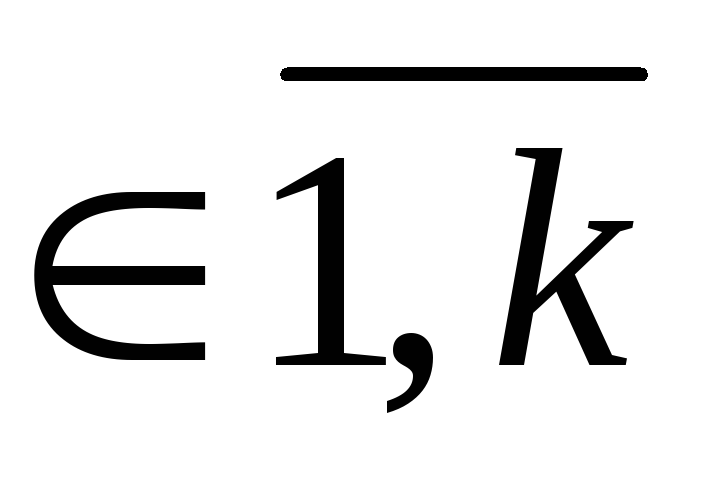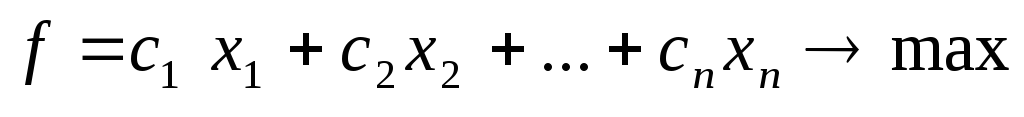- Тема 4.
- Цель изучения – получить представление о теории двойственности и осознать ее экономическую значимость.
- 4.1. Определение и экономический смысл двойственной злп
- 5. Двойственная задача линейного программирования. Экономическая интерпретация двойственной задачи линейного программирования.
- 1.5. Двойственная задача линейного программирования
- 1.5.1. Экономическая интерпретация двойственной задачи
- 2.7. Двойственная задача линейного программирования. Экономическая интерпретация
Тема 4.
Для изучения данного раздела дисциплины необходимы знания, полученные при изучении темы 3.
Изучив данную тему, студент должен:
- знать основные положения теории двойственности;
- уметь записывать двойственную задачу для любых постановок исходной задачи;
- иметь общие представления об анализе решения ЗЛП с помощью теории двойственности и анализе решения ЗЛП на основе отчетов MS EXCEL;
- использовать отчеты, полученные с помощью MS Excel, для анализа на чувствительность.
Цель изучения – получить представление о теории двойственности и осознать ее экономическую значимость.
В данном разделе вводится важное понятие теории линейного программирования – понятие двойственности. Двойственная задача – это вспомогательная задача линейного программирования (ЛП), формулируемая с помощью определённых правил непосредственно из условий исходной (прямой) задачи. Часто рассматриваются формулировки двойственной задачи, соответствующие различным формам записи прямой задачи. Однако опыт показывает, что на начальной стадии изучения ЛП детали различных формулировок двойственной задачи нередко затрудняют восприятие материала. Кроме того, практическое использование теории двойственности не требует знания деталей различных формулировок двойственной задачи. Здесь даётся обобщённая формулировка двойственной задачи ЛП, которая применима к любой форме представления прямой задачи. Это объясняется тем, что использование симплексного и других методов решения задач ЛП требует приведения ограничений любой задачи ЛП к стандартной (канонической) форме, поэтому двойственная задача будет сформулирована в соответствии со стандартной формой ограничений прямой задачи.
4.1. Определение и экономический смысл двойственной злп
Пусть прямая задача записана с ограничениями в каноническом виде: 








| Прямая задача | Двойственная задача | |
   P = P =  |    Q = Q =  –не ограничен в знаке –не ограничен в знаке | (4.7) |
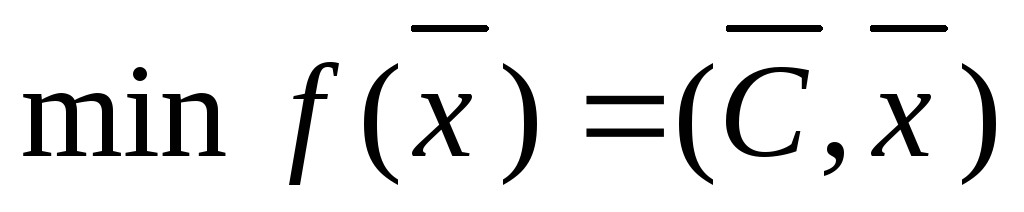   P = P =  |  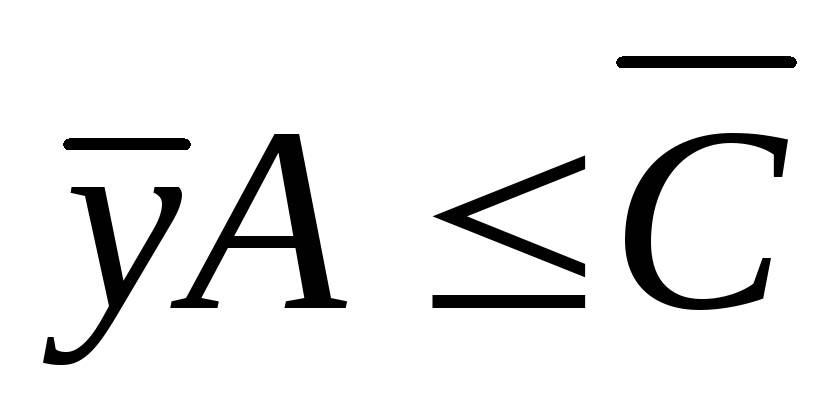  Q = Q =  не ограничен в знаке не ограничен в знаке | (4.8) |
Пример 4.1. Пусть прямая задача записана в виде основной ЗЛП:
  | (4.9) |
Приведем ограничения задачи (4.9) к канонической форме:
  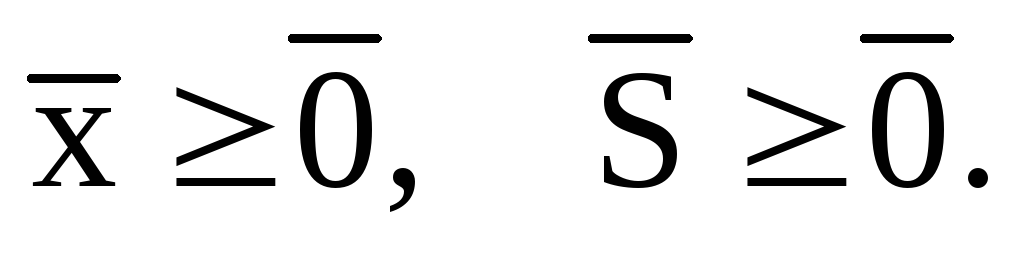 | (4.10) |
Тогда двойственная задача (ДЗ) будет иметь вид:
   . . | (4.11) |
Пример 4.2. Прямая задача: 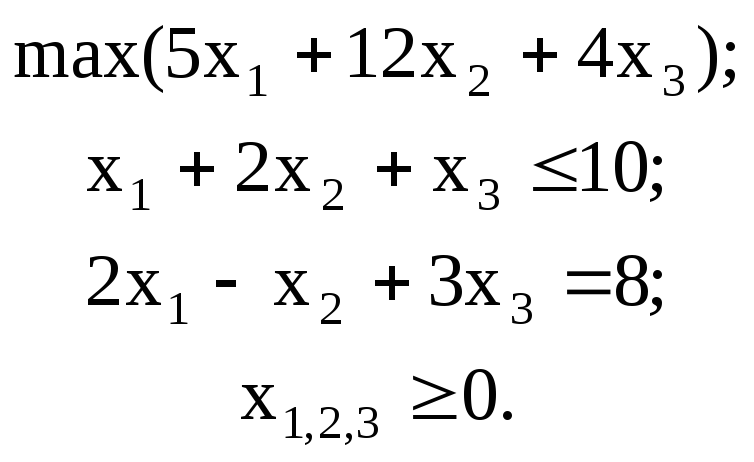

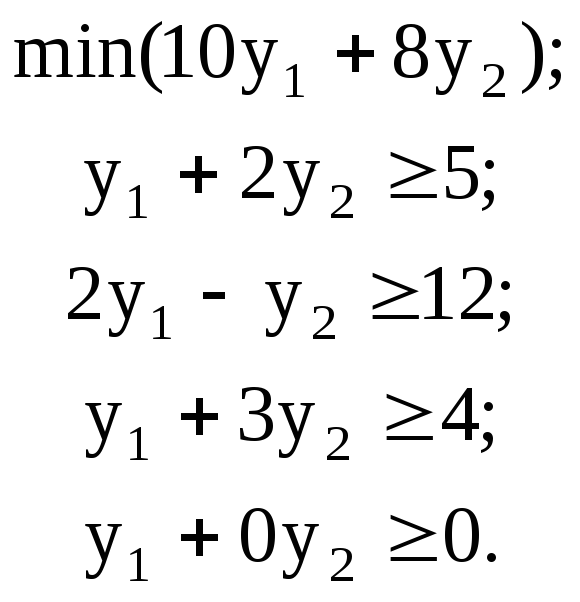









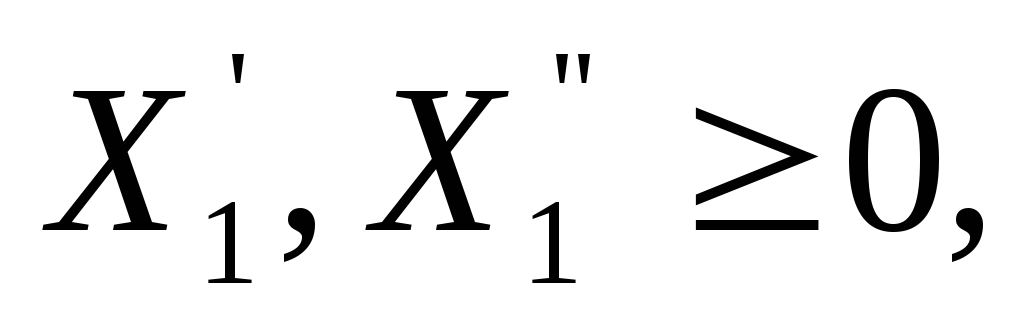

5. Двойственная задача линейного программирования. Экономическая интерпретация двойственной задачи линейного программирования.
1.5. Двойственная задача линейного программирования
Рассмотрим задачу линейного программирования
На основе тех же исходных данных может быть поставлена еще одна задача:
Сопоставим обе задачи. Первая из них — задача на максимум, вторая — задача на минимум; в соответствии с этим изменился и характер ограничений (знак неравенств). В первой задаче n неизвестных и k ограничений, во второй — k неизвестны х и n ограничений. Коэффициенты в целевых функциях и величины в правых частях неравенств при переходе от одной задачи к другой меняются местами. Кроме того, при этом переходе транспонируется матрица ограничений А.
Обе задачи образуют двойственную пару задач. Первую из них называют прямой задачей, а вторую —двoйсmвeннoй.
Общие правила построения двойственной задачи:
1) каждому ограничению исходной задачи соответствует двойственная переменная;
2) матрицы ограничений взаимно транспонированы;
3) правые части системы ограничений одной задачи являются коэффициентами при соответствующих переменных целевой функции другой задачи. При этом максимизация целевой функции заменяется на минимизацию, и наоборот.
4) каждому ограничению-неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности соответствующей двойственной переменной, а равенству — произвольная двойственная переменная.
В линейном программировании доказывается следующая основная теорема двойственности.
Теорема 1.8.Если одна из двойственных задач линейного программирования имеет решение, то имеет решение и другая. При этом значения целевых функций совпадают, т. е.
1.5.1. Экономическая интерпретация двойственной задачи
Для экономической интерпретации двойственной задачи будем полагать, например, что прямая задача — задача распределения ресурсов. Предположим, что в производстве используется kразличных видов ресурсов, объем которых ограничен величинамиbi. Может производитьсяnвидов продукции, величина выпуска которых характеризуется переменнымихi. Известны нормы затрат каждого ресурса на единицу каждого вида продукции —аij,а также стоимостная оценка единицы продукции —сj.
Переменные величины, подлежащие определению в двойственной задаче, являются оценки yi, предписываемые каждому виду ресурсов. Они должны быть такими, чтобы общая оценка всего имеющегося количества ресурсов была минимальной, но при условии, что суммарная оценка ресурсов, расходуемых на единицу любого вида продукции, будет не меньше, чем цена за эту единицу.
С экономической стороны решение прямой задачи дает оптимальный план выпуска продукции, а решение двойственной задачи — оптимальную систему условных оценок применяемых ресурсов.
Следующая теорема устанавливает связь между решениями двух задач.
Теорема 1.9.Пусть xi*. хn* и у1*. yk* — оптимальные планы двойственных задач. Тогда
1.Если ai1,xi* +. +аinхn* i(i), то уi* = 0.
2. Если уi* >0 (i),то ai1x1* +. +аinхn* =bi
Экономическое содержание: двойственные оценки не полностью используемых ресурсов всегда равны нулю; положительную двойственную оценку могут иметь лишь ресурсы, полностью используемые в оптимальном плане.
З.Если а1jy1* +. +akjyk* >сj(j),то хj*=0.
4.Если хj* > 0 (j),то а1jу1* +. + akjyk* =сj.
Экономическое содержание: если по двойственным оценкам производство данной продукции убыточно, то выпускать ее нерационально и она не вошла в оптимальный план; если данный вид продукции вошел в оптимальный план, то двойственная оценка затрачиваемых ресурсов равна ее цене и производство продукции по оценкам оправдано.
2.7. Двойственная задача линейного программирования. Экономическая интерпретация
Рассмотрим задачу линейного программирования следующего вида:
(2.7.1)
(2.7.2)
В задаче требуется максимизировать целевую функцию; все ограничения являются неравенствами со знаком 





Двойственная задача линейного программирования имеет вид
(2.7.3)
(2.7.4)
В двойственной задаче требуется найти минимум целевой функции, ограничения – неравенства со знаком 
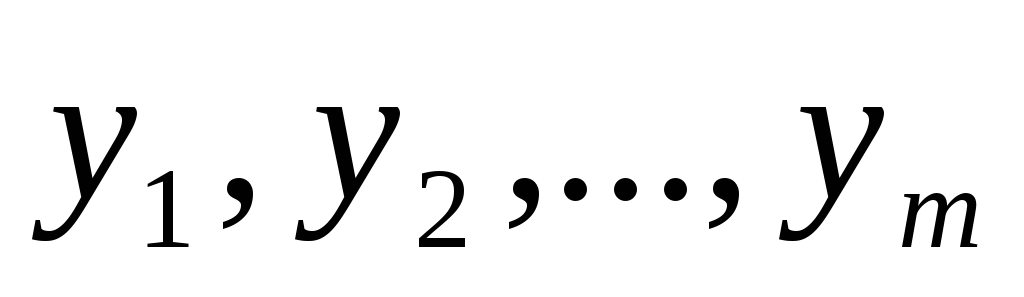

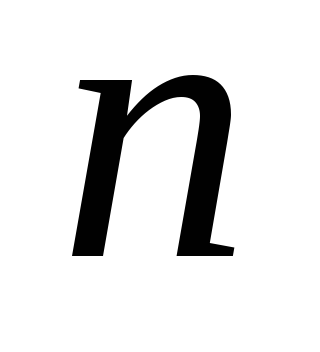


Задачи (2.7.1), (2.7.2) и (2.7.3), (2.7.4) называются парой взаимно двойственных задач линейного программирования.
Для двойственных задач верна следующая теорема.
Теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение х*, то другая также имеет оптимальное решение у*. При этом соответствующие им оптимальные значения целевых функций 

Поясним экономический смысл двойственной модели.
Пусть в качестве управляющих переменных 
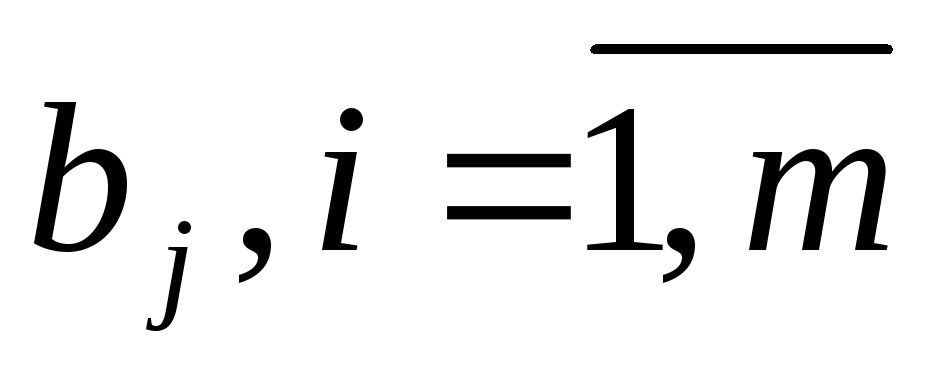

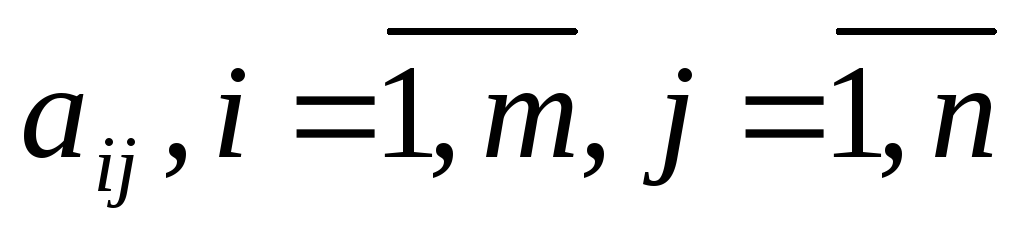
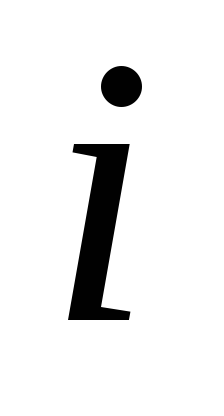



Пусть предприятие решило прекратить производство изделий и продать ресурсы, идущие на их изготовление. Обозначим через 




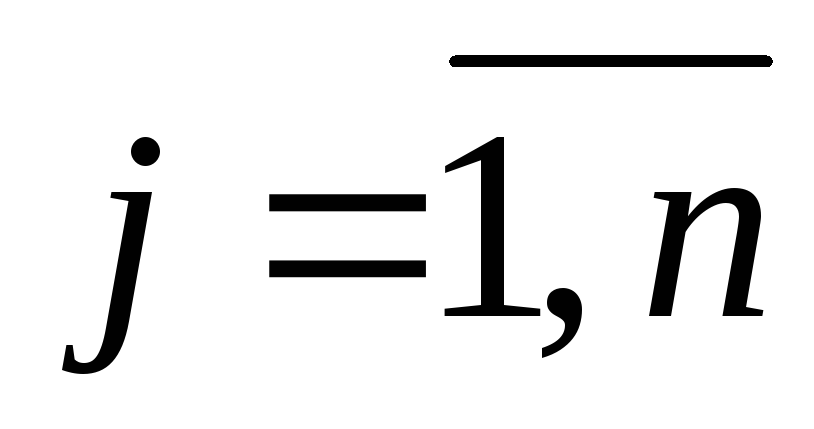

Построение двойственной задачи позволяет глубже разобраться в поставленной экономической проблеме.