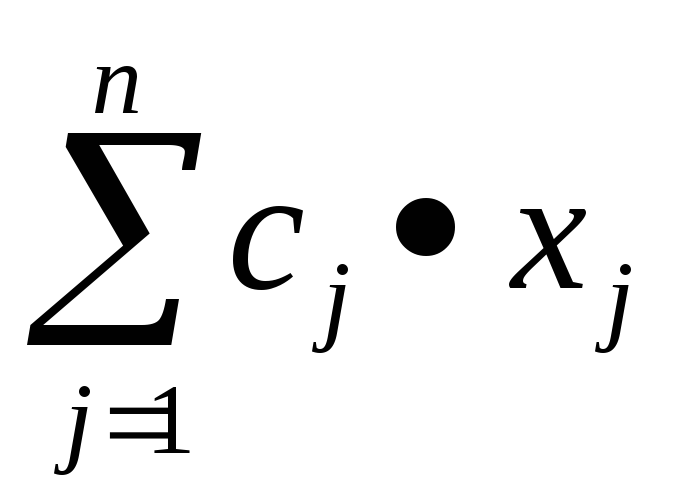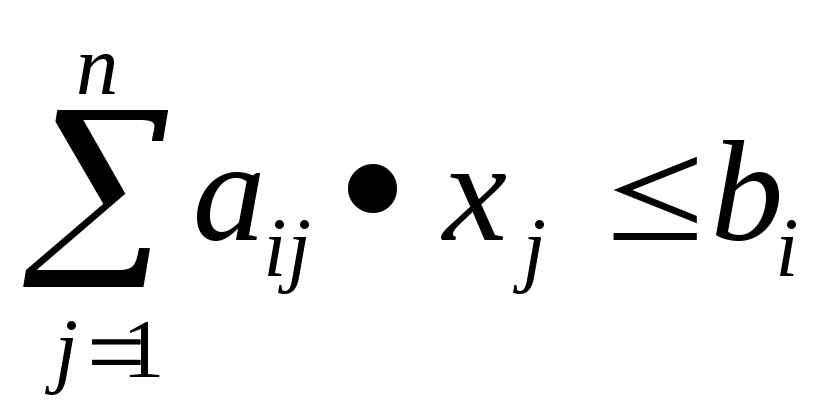Двойственная функция линейное программирование

Решение двойственной задачи линейного программирования

Инструкция . Выберите количество переменных и количество ограничений прямой задачи линейного программирования, нажмите Далее . Полученное решение сохраняется в файле Word и Excel . При этом ограничения типа x_i ≥ 0 не учитывайте. Если прямая задача ЛП не имеет решение, но требуется составить двойственную задачу или одна из переменных x_i неопределена, то можно использовать этот калькулятор.

Определив обратную матрицу А -1 через алгебраические дополнения, получим:
Как видно из последнего плана симплексной таблицы, обратная матрица A -1 расположена в столбцах дополнительных переменных x₄ , x₅ , x₆ .
Тогда Y = C*A -1 =
Оптимальный план двойственной задачи равен: y₁ = 23.75, y₂ = 12.5, y₃ = 0
Z(Y) = 1100*23.75+120*12.5+8000*0 = 27625
Подставим оптимальный план прямой задачи в систему ограниченной математической модели:
0.1*250 + 0.2*5375 + 0.4*0 = 1100 = 1100
0.05*250 + 0.02*5375 + 0.02*0 = 120 = 120
3*250 + 1*5375 + 2*0 = 6125 < 8000 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₁>0).
2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y₃ = 0.
Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов.
При постановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим:
0.1*23.75 + 0.05*12.5 + 3*0 = 3 = 3
0.2*23.75 + 0.02*12.5 + 1*0 = 5 = 5
0.4*23.75 + 0.02*12.5 + 2*0 = 9.75 > 4
1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₁>0).
2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x₂>0).
3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x₃ = 0.
Величина двойственной оценки показывает, на сколько возрастает значение целевой функции при увеличении дефицитного ресурса на единицу.
Например, увеличении 1-го ресурса на 1 приведет к получению нового оптимального плана, в котором целевая функция возрастает на 23.75 и станет равной: F(x) = 27625 + 23.75 = 27648.75
Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции.
Пусть каждое значение параметра целевой функции изменится на ∆ с_i. Найдем интервалы, при которых будет экономически выгодно использование ресурсов.
1-ый параметр целевой функции может изменяться в пределах:

-3.8 ≤ с₁ ≤ 1
Таким образом, 1-параметр может быть уменьшен на 3.8 или увеличен на 1
Интервал изменения равен: [3-3.8; 3+1] = [-0.8;4]
Если значение c₁ будет лежать в данном интервале, то оптимальный план не изменится. 2-ый параметр целевой функции может изменяться в пределах:

-10 ≤ b₂ ≤ 30
Таким образом, 2-ый запас может быть уменьшен на 10 или увеличен на 30
Интервал изменения равен: [120-10; 120+30] = [110;150]
Составим субоптимальные варианты плана с учетом изменений исходных данных модели (таблицы).
Пусть 2-ый ресурс увеличили на 50

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (50)	Расчет варианта плана
x 2	5375	6.25	312.5	5687.5
x 1	250	-2.5	-125	125
x 6	1875	1.25	62.5	1937.5
F(X)	27625	23.75	1187.5	28812.5

Пусть 1-ый ресурс уменьшили на -5

Базисные переменные	Значение базисных переменных	Коэффициент структурных сдвигов k c	Произведение k c на (-5)	Расчет варианта плана
x 2	5375	-12.5	62.5	5437.5
x 1	250	25	-125	125
x 6	1875	-62.5	312.5	2187.5
F(X)	27625	12.5	-62.5	27562.5

Задание : Для исходной задачи составить двойственную. Решить обе задачи симплексным методом или двойственным симплексным методом и по решению каждой из них найти решение другой. Одну из задач решить графическим методом.
F(X) = 3x₁ + x₂ → min
— 2x₁ + x₂≥4
2x₁ + x₂≤8
3x₁ + 2x₂≥6
Решение.
I этап. Приводим систему к каноническому виду.
II этап. Решаем симплекс-методом.
Примечание: Если задача решается данным калькулятором, то предыдущие два этапа пропускаем, поскольку они автоматически включены в решение.
На втором этапе окончательный вариант симплекс-таблицы имеет вид:

Базис	B	x₁	x₂	x₃	x₄	x₅	x₆	x₇
x₅	2	-7	0	-2	0	1	2	-1
x₄	4	4	0	1	1	0	-1	0
x₂	4	-2	1	-1	0	0	1	0
F(X3)	4	-5	0	-1	0	0	1-M	-M

Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Записываем оптимальный план:
x₁ = 0, x₂ = 4, F(X) = 1•4 = 4 Составим двойственную задачу к прямой задаче.
— 2y₁ + 2y₂ + 3y₃≤3
y₁ + y₂ + 2y₃≤1
4y₁ + 8y₂ + 6y₃ → max
y₁ ≥ 0, y₂ ≤ 0, y₃ ≥ 0
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из теоремы двойственности следует, что Y = C*A -1 . Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

Источник

3. 2 Двойственность в задачах линейного программирования

Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования.

Экономическая интерпретация задачи, двойственной задаче об использовании ресурсов. Ранее рассмотрена задача об использовании ресурсов (экономико-математическая модель и содержательная интерпретация этой задачи I представлены в левой части табл. 6.1). В приведенной модели b_i (i = 1, 2, . m) обозначает запас ресурса S_i , a_ij — число единиц ресурса S_i потребляемого при производстве единицы продукции P_j(j = 1, 2, . n); C_j — прибыль (выручка) от реализации единицы продукции Pj (или цена продукции Pj). Предположим, что некоторая организация решила закупить ресурсы S₁, S₂, . S_m предприятия и необходимо установить оптимальные цены на эти ресурсы у₁, у₂, . y_m Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах b₁, b₂, . b_m по ценам соответственно у₁, у₂, . y_mбыли минимальны, т.е Z=b₁у₁ + b₂ у₂ +. + b_m у_m min . С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы продукции Р₁ расходуется a₁₁ единиц ресурса S₁, a₂₁ единиц ресурса S₂, . a_i1единиц ресурса S_i . а_m1 единиц ресурса S_m по цене соответственно у₁, у₂, . у_i . y_m. Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции Р₁ должны быть не менее ее цены c₁, т.е. a₁₁ у₁ + a₂₁ у₂ +:+a_m1 у_m>=c₁ Аналогично можно составить ограничения в виде неравенств по каждому виду продукции Р₁, Р₂, . Р_m. Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи II приведены в правой части табл. 6.1.

Задача II (двойственная)

F=c₁x₁+c₂x ₂+. +c_nx_nmax (6.1) при ограничениях a₁₁x₁ + a₁₂x₂+. + a_1nx_n ₁ a₂₁x₁ + a₂₂x₂+. + a _2nx_n ₂ (6.2) a_m1x₁ + a_m2x₂+. + a_mnx_n _m и условии неотрицательности x₁>= 0; x₂>= 0;: x_n>= 0 Составить такой план выпуска продукции Х = (х₁, х₂, . х_n), при котором прибыль (выручка) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.

Z=b₁y₁+b₂y₂+. +b_m y_m min (6.4) при ограничениях a₁₁у₁ + a₂₁у₂+. + a_m1у_m >= c₁ a₁₂у₁ + a₂₂у₂+. + a_m2у_m >= c₂ (6.5) a_1nу₁ + a_2nу₂+. + a_mnу_m >= c_n и условии неотрицательности. y₁>= 0; y₂>= 0;: y_m>= 0 Найти такой набор цен (оценок) ресурсов Y = (у₁, y₂, . у_m), при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции

Цены ресурсов у₁, у₂, . у_m в экономической литературе получили различные названия: учетные, неявные, теневые. Смысл этих названий состоит в том, что этоусловные, «ненастоящие» цены. В отличие от «внешних» цен c₁, с₂, . c_n на продукцию, известных, как правило, до начала производства, цены ресурсов у₁, у₂, . у_nявляются внутренними, ибо они задаются не извне, а определяются непосредственно в результате решения задачи, поэтому их чаще называют оценками ресурсов.