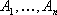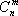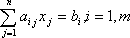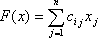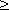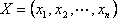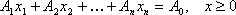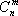Допустимая задача математического линейного программирования

Решение задач линейного программирования

Назначение сервиса . Онлайн-калькулятор предназначен для решения задач линейного программирования симплексным методом путем перехода к КЗЛП и СЗЛП . При этом задача на минимум целевой функции сводятся к задаче на поиск максимума через преобразование целевой функции F*(X) = -F(X) . Также имеется возможность составить двойственную задачу.

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Инструкция . Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word .

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min

F(x) → max

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Пример №1 . Свести задачу линейного программирования к стандартной ЗЛП.
F(X) = x₁ + 2x₂ — 2x₃ → min при ограничениях:
4x₁ + 3x₂ — x₃≤10
— 2x₂ + 5x₃≥3
x₁ + 2x₃=9
Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции. Сведем задачу F(X) → min к задаче F(X) → max. Для этого умножаем F(X) на (-1). В первом неравенстве смысла (≤) вводим базисную переменную x₄; во втором неравенстве смысла (≥) вводим базисную переменную x₅ со знаком минус.
4x₁ + 3x₂-1x₃ + 1x₄ + 0x₅ = 10
0x₁-2x₂ + 5x₃ + 0x₄-1x₅ = 3
1x₁ + 0x₂ + 2x₃ + 0x₄ + 0x₅ = 9
F(X) = — x₁ — 2x₂ + 2x₃
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:

4	3	-1	1	0	10
0	-2	5	0	-1	3
1	0	2	0	0	9

Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x₄.
2. В качестве базовой переменной выбираем x₂.
Разрешающий элемент РЭ=-2. Строка, соответствующая переменной x₂, получена в результате деления всех элементов строки x₂ на разрешающий элемент РЭ=-2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(0 • 3):-2	3-(-2 • 3):-2	-1-(5 • 3):-2	1-(0 • 3):-2	0-(-1 • 3):-2	10-(3 • 3):-2
0 : -2	-2 : -2	5 : -2	0 : -2	-1 : -2	3 : -2
1-(0 • 0):-2	0-(-2 • 0):-2	2-(5 • 0):-2	0-(0 • 0):-2	0-(-1 • 0):-2	9-(3 • 0):-2

Получаем новую матрицу:

4	0	6 1 /2	1	-1 1 /2	14 1 /2
0	1	-2 1 /2	0	1 /2	-1 1 /2
1	0	2	0	0	9

3. В качестве базовой переменной выбираем x₃.
Разрешающий элемент РЭ=2. Строка, соответствующая переменной x₃, получена в результате деления всех элементов строки x₃ на разрешающий элемент РЭ=2. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₃ записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:

4-(1 • 6 1 /2):2	0-(0 • 6 1 /2):2	6 1 /2-(2 • 6 1 /2):2	1-(0 • 6 1 /2):2	-1 1 /2-(0 • 6 1 /2):2	14 1 /2-(9 • 6 1 /2):2
0-(1 • -2 1 /2):2	1-(0 • -2 1 /2):2	-2 1 /2-(2 • -2 1 /2):2	0-(0 • -2 1 /2):2	1 /2-(0 • -2 1 /2):2	-1 1 /2-(9 • -2 1 /2):2
1 : 2	0 : 2	2 : 2	0 : 2	0 : 2	9 : 2

Получаем новую матрицу:

3 /4	0	0	1	-1 1 /2	-14 3 /4
1 1 /4	1	0	0	1 /2	9 3 /4
1 /2	0	1	0	0	4 1 /2

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,2,3).
Соответствующие уравнения имеют вид:
3 /₄x₁ + x₄ — 1 1 /₂x₅ = -14 3 /₄
1 1 /₄x₁ + x₂ + 1 /₂x₅ = 9 3 /₄
1 /₂x₁ + x₃ = 4 1 /₂
Выразим базисные переменные через остальные:
x₄ = — 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄
x₂ = — 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄
x₃ = — 1 /₂x₁+4 1 /₂
Подставим их в целевую функцию:
F(X) = — x₁ — 2(- 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄) + 2(- 1 /₂x₁+4 1 /₂)
или
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Система неравенств:
— 3 /₄x₁ + 1 1 /₂x₅-14 3 /₄ ≥ 0
— 1 1 /₄x₁ — 1 /₂x₅+9 3 /₄ ≥ 0
— 1 /₂x₁+4 1 /₂ ≥ 0
Приводим систему неравенств к следующему виду:
3 /₄x₁ — 1 1 /₂x₅ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₅ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₅-10 1 /₂ → max
Упростим систему.
3 /₄x₁ — 1 1 /₂x₂ ≤ -14 3 /₄
1 1 /₄x₁ + 1 /₂x₂ ≤ 9 3 /₄
1 /₂x₁ ≤ 4 1 /₂
F(X) = 1 /₂x₁ + x₂-10 1 /₂ → max

Источник

Математические модели задач линейного программирования

Переменными задачи называются величины Х1, Х2, Хn, которые полностью характеризуют экономический процесс. Обычно их записывают в виде вектора: X=(X₁, X₂. X_n).

Системой ограничений задачи называют совокупность уравнений и неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче.

Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

В общем случае задача линейного программирования может быть записана в таком виде:

Данная запись означает следующее: найти экстремум целевой функции (1) и соответствующие ему переменные X=(X₁, X₂. X_n) при условии, что эти переменные удовлетворяют системе ограничений (2) и условиям неотрицательности (3).

Допустимым решением (планом) задачи линейного программирования называется любой n-мерный вектор X=(X₁, X₂. X_n), удовлетворяющий системе ограничений и условиям неотрицательности.

Множество допустимых решений (планов) задачи образует область допустимых решений (ОДР).

Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.

Пример составления математической модели

Задача использования ресурсов (сырья)

Условие: Для изготовления n видов продукции используется m видов ресурсов. Составить математическую модель.

• b_i ( i = 1,2,3. m) — запасы каждого i-го вида ресурса;
• a_ij ( i = 1,2,3. m; j=1,2,3. n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции;
• c_j ( j = 1,2,3. n) — прибыль от реализации единицы объема j-го вида продукции.

Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье).

Введем вектор переменных X=(X₁, X₂. X_n), где x_j ( j = 1,2. n) — объем производства j-го вида продукции.

Затраты i-го вида ресурса на изготовление данного объема x_j продукции равны a_ijx_j, поэтому ограничение на использование ресурсов на производство всех видов продукции имеет вид:
Прибыль от реализации j-го вида продукции равна c_jx_j , поэтому целевая функция равна:

Ответ — Математическая модель имеет вид:

Источник

Общая задача линейного программирования.

3) цель задачи ()

(max F(x))

(min F(x))

Определение: Планом или допустимым решением задачи линейного программирования называется вектор , удовлетворяющий условиям 1) и 2)

(*)

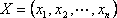
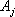
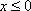
Определение: План называетсяопорным, если векторы , входящие в разложение (*) с положительными коэффициентами, являются линейно независимыми.

Определение: Опорный план называется невырожденным, если он содержит m – положительных компонентов, в противном случае опорный план называется вырожденным.

Определение: Оптимальным планом (решением) задачи линейного программирования называется план, доставляющий линейной форме наибольшее или наименьшее значение.

В большинстве задач ограничения задаются не в виде системы уравнений, а в виде системы линейных неравенств, либо система ограничений смешанная, однако любую систему ограничений можно привести к системе уравнений. Для этого достаточно к левой части каждого неравенства прибавить (для ) или отнять (для) какое-то неотрицательное число (добавочную переменную) с тем, чтобы каждое неравенство обратилось в уравнение, в результате получим эквивалентные системы уравнений и неравенств.

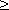
Основные теоремы линейного программирования

Теорема 1: Множество всех допустимых решений системы ограничений задачи линейного программирования, является выпуклым.

Теорема 2: Если существует, и при том единственное, оптимальное решение задачи линейного программирования, то оно совпадает с одной из угловых точек множества допустимых решений. Если линейная форма принимает минимальное (максимальное) значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Из теоремы 2 следует, что поиски оптимального решения можно ограничить перебором конечного числа угловых точек (их число меньше , гдеn — число неизвестных , а m – число ограничений), однако построение возможно только для двух и трёхмерных пространств, поэтому нужны аналитические методы, позволяющие находить координаты угловых точек.

Теорема 3: Если известно, что система векторов в разложении линейно независима и такова, что, где, то точкаявляется угловой точкой многогранника решений.

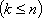
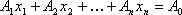
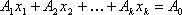
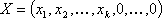
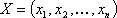
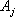
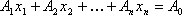
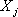
Теорема 4: Если — угловая точка многогранника решений, то векторыв разложении, соответствующие положительным, являются линейно независимыми.

Следствие 1: Так как векторы 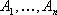имеют размерностьm, то угловая точка многогранника решений имеет не более m положительных компонент .

Следствие 2: Каждой угловой точке многогранника решений соответствует линейно независимых векторов системы векторов.

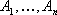
Симплексный метод решения задачи линейного программирования.

Доказано, что оптимальное решение задачи линейного программирования связано с угловыми точками многоугольника решений, то есть с опорными планами. Они определяются системой m — линейно независимых векторов, содержащихся в системе из n — векторов. Количество опорных планов меньше, гдеn — число неизвестных, а m – число ограничений. При больших n и m найти все их перебором очень трудно, поэтому необходимо упорядоченный перебор, такой схемой является симплексный метод, который позволяет исходя из известного опорного плана задачи, за конечное число шагов получить её оптимальный план. Каждый из шагов (итераций) состоит в нахождении нового плана, которому соответствует меньшее для задачи на минимум (большее для задачи на максимум) значение линейной формы, чем её значение в предыдущем плане. Процесс продолжается до получения оптимального плана. Если задача не обладает планами или её линейная форма неограниченна на многограннике решений, то симплексный метод позволяет установить это в процессе решения.

Источник