Динамическое программирование. Классические задачи
Здравствуй, Хабрахабр. В настоящий момент я работаю над учебным пособием по олимпиадному программированию, один из параграфов которого посвящен динамическому программированию. Ниже приведена выдержка из данного параграфа. Пытаясь объяснить данную тему как можно проще, я постарался сложные моменты сопроводить иллюстрациями. Мне интересно ваше мнение о том, насколько понятным получился данный материал. Также буду рад советам, какие еще задачи стоит включить в данный раздел.
Во многих олимпиадных задачах по программированию решение с помощью рекурсии или полного перебора требует выполнения очень большого числа операций. Попытка решить такие задачи, например, полным перебором, приводит к превышению времени выполнения.
Однако среди переборных и некоторых других задач можно выделить класс задач, обладающих одним хорошим свойством: имея решения некоторых подзадач (например, для меньшего числа n), можно практически без перебора найти решение исходной задачи.
Такие задачи решают методом динамического программирования, а под самим динамическим программированием понимают сведение задачи к подзадачам.
Последовательности
Классической задачей на последовательности является следующая.
Последовательность Фибоначчи Fn задается формулами: F1 = 1, F2 = 1,
Fn = Fn – 1 + Fn – 2 при n > 1. Необходимо найти Fn по номеру n.
Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:
Используя такую функцию, мы будем решать задачу «с конца» — будем шаг за шагом уменьшать n, пока не дойдем до известных значений.
Но как можно заметить, такая, казалось бы, простая программа уже при n = 40 работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.
Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования:
Приведенное решение является корректным и эффективным. Но для данной задачи применимо и более простое решение:
Такое решение можно назвать решением «с начала» — мы первым делом заполняем известные значения, затем находим первое неизвестное значение (F3), потом следующее и т.д., пока не дойдем до нужного.
Именно такое решение и является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все Fi для i < n), затем, зная решения подзадач, нашли ответ (Fn = Fn – 1 + Fn – 2, Fn – 1 и Fn – 2 уже найдены).
Одномерное динамическое программирование
Чтобы лучше понять суть динамического программирования, сначала более формально определим понятия задачи и подзадачи.
Пусть исходная задача заключается в нахождении некоторого числа T при исходных данных n1, n2, . nk. То есть мы можем говорить о функции T(n1, n2, . nk), значение которой и есть необходимый нам ответ. Тогда подзадачами будем считать задачи
T(i1, i2, . ik) при i1 < n1, i2 < n2, . ik < nk.
Далее мы будем о говорить об одномерном, двумерном и многомерном динамическом программировании при k = 1, k = 2, k > 2, соответственно.
Следующая задача одномерного динамического программирования встречается в различных вариациях.
Задача 1. Посчитать число последовательностей нулей и единиц длины n, в которых не встречаются две идущие подряд единицы.
При n = 1, n = 2 ответ очевиден. Допустим, что мы уже нашли Kn – 1, Kn – 2 — число таких последовательностей длины n – 1 и n – 2.
Посмотрим, какой может быть последовательность длины n. Если последний ее символ равен 0, то первые n – 1 — любая правильная последовательность длины
n – 1 (не важно, заканчивается она нулем или единицей — следом идет 0). Таких последовательностей всего Kn – 1. Если последний символ равен 1, то предпоследний символ обязательно должен быть равен 0 (иначе будет две единицы подряд), а первые
n – 2 символа — любая правильная последовательность длины n – 2, число таких последовательностей равно Kn – 2.
Таким образом, K1 = 2, K2 = 3, Kn = Kn – 1 + Kn – 2 при n > 2. То есть данная задача фактически сводится к нахождению чисел Фибоначчи.
Двумерное динамическое программирование
Классической задачей двумерного динамического программирования является задача о маршрутах на прямоугольном поле.
В разных формулировках необходимо посчитать число маршрутов или найти маршрут, который является лучшим в некотором смысле.
Приведем пару формулировок таких задач:
Задача 2. Дано прямоугольное поле размером n*m клеток. Можно совершать шаги длиной в одну клетку вправо или вниз. Посчитать, сколькими способами можно попасть из левой верхней клетки в правую нижнюю.
Задача 3. Дано прямоугольное поле размером n*m клеток. Можно совершать шаги длиной в одну клетку вправо, вниз или по диагонали вправо-вниз. В каждой клетке записано некоторое натуральное число. Необходимо попасть из верхней левой клетки в правую нижнюю. Вес маршрута вычисляется как сумма чисел со всех посещенных клеток. Необходимо найти маршрут с минимальным весом.
Для всех таких задач характерным является то, что каждый отдельный маршрут не может пройти два или более раз по одной и той же клетке.
Рассмотрим более подробно задачу 2. В некоторую клетку с координатами (i,j) можно прийти только сверху или слева, то есть из клеток с координатами (i – 1, j) и (i, j – 1):
Таким образом, для клетки (i, j) число маршрутов A[i][j] будет равно
A[i – 1][j] + A[i][j – 1], то есть задача сводится к двум подзадачам. В данной реализации используется два параметра — i и j — поэтому применительно к данной задаче мы говорим о двумерном динамическом программировании.
Теперь мы можем пройти последовательно по строкам (или по столбцам) массива A, находя число маршрутов для текущей клетки по приведенной выше формуле. Предварительно в A[0][0] необходимо поместить число 1.
В задаче 3 в клетку с координатами (i, j) мы можем попасть из клеток с координатами
(i – 1, j), (i, j – 1) и (i – 1, j – 1). Допустим, что для каждой из этих трех клеток мы уже нашли маршрут минимального веса, а сами веса поместили в W[i – 1][j], W[i][j – 1],
W[i – 1][j – 1]. Чтобы найти минимальный вес для (i, j), необходимо выбрать минимальный из весов W[i – 1][j], W[i][j – 1], W[i – 1][j – 1] и прибавить к нему число, записанное в текущей клетке:
W[i][j] = min(W[i–1][j], W[i][j – 1], W[i – 1][j – 1]) + A[i][j];
Данная задача осложнена тем, что необходимо найти не только минимальный вес, но и сам маршрут. Поэтому в другой массив мы дополнительно для каждой клетки будем записывать, с какой стороны в нее надо попасть.
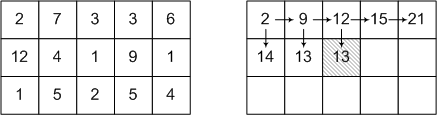
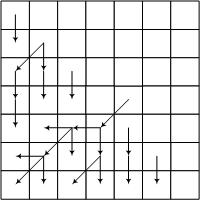
На следующем рисунке приведен пример исходных данных и одного из шагов алгоритма.
В каждую из уже пройденных клеток ведет ровно одна стрелка. Эта стрелка показывает, с какой стороны необходимо прийти в эту клетку, чтобы получить минимальный вес, записанный в клетке.
После прохождения всего массива необходимо будет проследить сам маршрут из последней клетки, следуя по стрелкам в обратную сторону.
Задачи на подпоследовательности
Рассмотрим задачу о возрастающей подпоследовательности.
Задача 4. Дана последовательность целых чисел. Необходимо найти ее самую длинную строго возрастающую подпоследовательность.
Начнем решать задачу с начала — будем искать ответ, начиная с первых членов данной последовательности. Для каждого номера i будем искать наибольшую возрастающую подпоследовательность, оканчивающуюся элементом в позиции i. Пусть исходная последовательность хранится в массиве A. В массиве L будем записывать длины максимальных подпоследовательностей, оканчивающихся текущим элементом. Пусть мы нашли все L[i] для 1 i k – 1. Теперь можно найти L[k] следующим образом. Просматриваем все элементы A[i] для 1 i < k – 1. Если
A[i] < A[k], то k-ый элемент может стать продолжением подпоследовательности, окончившейся элементом A[i]. Длина полученной подпоследовательности будет на 1 больше L[i]. Чтобы найти L[k], необходимо перебрать все i от 1 до k – 1:
L[k] = max(L[i]) + 1, где максимум берется по всем i таким, что A[i] < A[k] и
1 i < k.
Здесь максимум из пустого множества будем считать равным 0. В этом случае текущий элемент станет единственным в выбранной последовательности, а не будет продолжением одной из предыдущих. После заполнения массива L длина наибольшей возрастающей подпоследовательности будет равна максимальному элементу L.
Чтобы восстановить саму подпоследовательность, можно для каждого элемента также сохранять номер предыдущего выбранного элемента, например, в массив N.
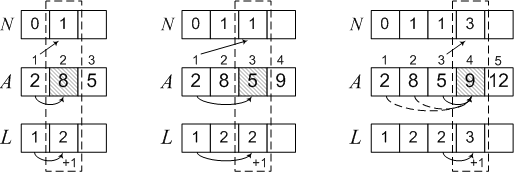
Рассмотрим решение этой задачи на примере последовательности 2, 8, 5, 9, 12, 6. Поскольку до 2 нет ни одного элемента, то максимальная подпоследовательность содержит только один элемент — L[1] = 1, а перед ним нет ни одного — N[1] = 0. Далее,
2 < 8, поэтому 8 может стать продолжением последовательности с предыдущим элементом. Тогда L[2] = 2, N[2] = 1.
Меньше A[3] = 5 только элемент A[1] = 2, поэтому 5 может стать продолжением только одной подпоследовательности — той, которая содержит 2. Тогда
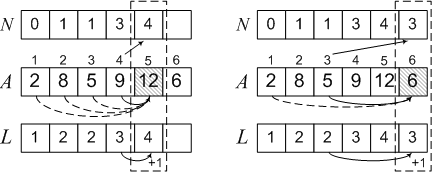
L[3] = L[1] + 1 = 2, N[3] = 1, так как 2 стоит в позиции с номером 1. Аналогично выполняем еще три шага алгоритма и получаем окончательный результат.
Теперь выбираем максимальный элемент в массиве L и по массиву N восстанавливаем саму подпоследовательность 2, 5, 9, 12.
Еще одной классической задачей динамического программирования является задача о палиндромах.
Задача 5. Дана строка из заглавных букв латинского алфавита. Необходимо найти длину наибольшего палиндрома, который можно получить вычеркиванием некоторых букв из данной строки.
Начнем решать задачу с самых простых подстрок. Для строки из одного символа (то есть подстроки вида S(i, i)) ответ очевиден — ничего вычеркивать не надо, такая строка будет палиндромом. Для строки из двух символов S(i, i + 1) возможны два варианта: если символы равны, то мы имеем палиндром, ничего вычеркивать не надо. Если же символы не равны, то вычеркиваем любой.
Пусть теперь нам дана подстрока S(i, j). Если первый (S[i]) и последний (S[j]) символы подстроки не совпадают, то один из них точно нужно вычеркнуть. Тогда у нас останется подстрока S(i, j – 1) или S(i + 1, j) — то есть мы сведем задачу к подзадаче: L[i][j] = max(L[i][j – 1], L[i + 1][j]). Если же первый и последний символы равны, то мы можем оставить оба, но необходимо знать решение задачи S(i + 1, j – 1):
L[i][j] = L[i + 1][j – 1] + 2.
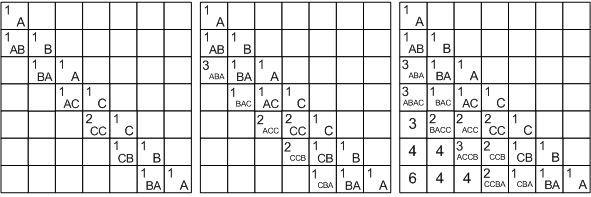
Рассмотрим решение на примере строки ABACCBA. Первым делом заполняем диагональ массива единицами, они будут соответствовать подстрокам S(i, i) из одного символа. Затем начинаем рассматривать подстроки длины два. Во всех подстроках, кроме S(4, 5), символы различны, поэтому в соответствующие ячейки запишем 1, а в L[4][5] — 2.
Получается, что мы будем заполнять массив по диагоналям, начиная с главной диагонали, ведущей из левого верхнего угла в правый нижний. Для подстрок длины 3 получаются следующие значения: в подстроке ABA первая и последняя буквы равны, поэтому
L[1][3] = L[2][2] + 2. В остальных подстроках первая и последняя буквы различны.
BAC: L[2][4] = max(L[2][3], L[3][4]) = 1.
ACC: L[3][5] = max(L[3][4], L[4][5]) = 2.
CCB: L[4][6] = max(L[4][5], L[5][6]) = 2.
CBA: L[5][7] = max(L[5][6], L[6][7]) = 1.
Продолжая далее аналогичные рассуждения, заполним все ячейки под диагональю и в ячейке L[1][7] = 6 получим ответ.
Если же в задаче необходимо вывести не длину, а сам палиндром, то дополнительно к массиву длин мы должны построить массив переходов — для каждой ячейки запомнить, какой из случаев был реализован (на рисунке для наглядности вместо числовых значений, кодирующих переходы, нарисованы соответствующие стрелки).