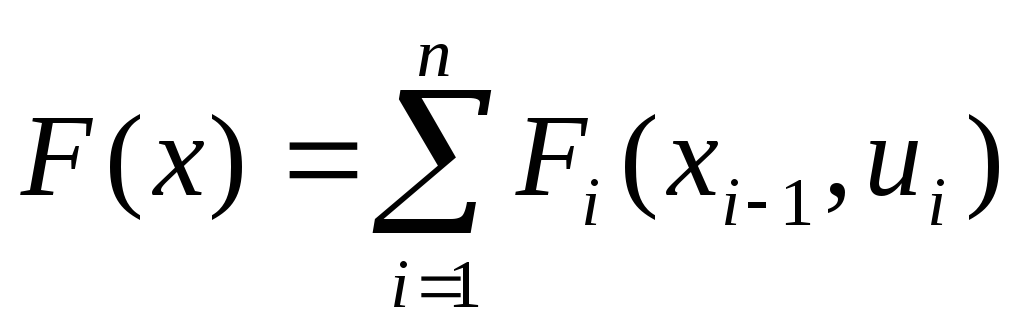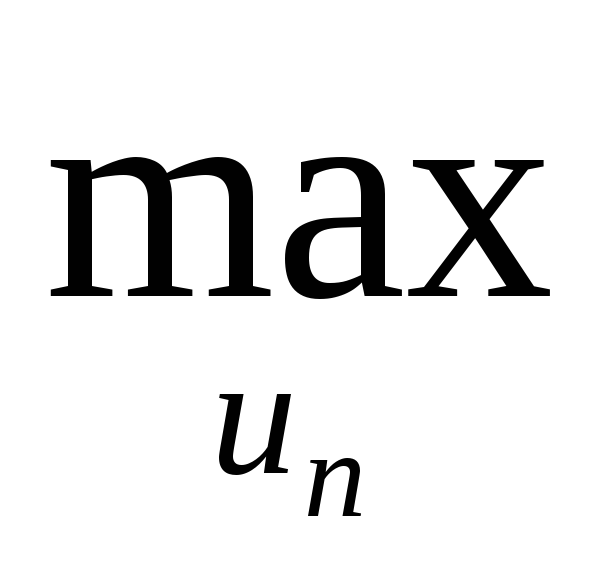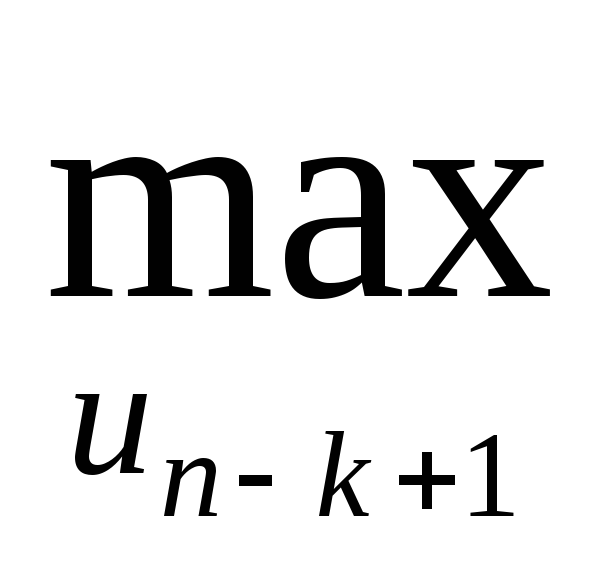Динамическое программирование обратный ход

Лекция 7,8. Метод динамического программирования.

Вопросы: 1. Основные понятия. Общая постановка задачи ДП.

2. Принцип оптимальности. Функциональные уравнения Беллмана.

3. Задача оптимального распределения ресурсов.

5. Задача управления производством и запасами.

1.Основные понятия. Общая постановка задачи динамического программирования.

Динамическое программирование — метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы, шаги.

Такие операции называются многошаговыми. Многие экономические процессы расчленяются на шаги естественным образом. Это процессы планирования и управления, развиваемые во времени. Естественным шагом может быть год, квартал, месяц и т.д. Т.о., если управление сводится к однократному принятию решения, то соответствующая задача называется одноэтапной или одношаговой. Ранее решаемые задачи линейного и нелинейного программирования – примеры подобных задач.Если управление требует некоторой последовательности принятых решений, то такая задача называется многоэтапной или многошаговой.

Рассмотрим некоторую управляемую систему, характеризующуюся определенным набором параметров, задающих ее состояния. Система под влиянием управления переходит из начального состояния в конечное. Введем обозначения.

1. x_i–многомерный вектор, компоненты которого определяют состояние системы на

i-том шаге. Дальнейшее изменение состояния зависит только от данного состояния и не

зависит от того, каким путем система перешла в него (процесс без последствия).

2.На каждом шаге выбирается одно решение,управление u_i, под действием которого

система переходит из предыдущего состояния x_i-1 в новое x_i. Это новое состояние

является функцией состояния на начало шага x_i-1и принятого в начале решенияu_i, т.е.

3. Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью)

или потерей (издержками), которые зависят от состояния на начало шага и принятого

решения. F_i – приращение целевой функции задачи в результате i-того шага,

аналогично, F_i = F_i ( x_i-1 , u_i ).Тогда значение целевой функции при переходе системы

из начального состояния в конечное за nшагов

.

4.На векторы состояния х_iи управленияu_iмогут быть наложены ограничения,

объединение которых составляет область допустимых решений uU.

5.Требуется найти такое допустимое управлениеu* = (u₁* ,…,u_n* ) (для каждого шага),

чтобы получить экстремальное значение функции цели F* за всеnшагов.

Любая последовательность действий для каждого шага, переводящая систему из начального состояния в конечное, называется стратегией управления.

Допустимая стратегия управления, доставляющая функции цели экстремальное значение, называется оптимальной.

2. Принцип оптимальности. Функциональные уравнения Беллмана.

Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, т.к. управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом. В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом.

Принцип оптимальности: если некоторая последовательность решений оптимальна, то на любом шаге последующие решения образуют оптимальную стратегию по отношению к результату предыдущих решений.

Другими словами, каково бы не было состояние системы перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге (проигрыш) плюс оптимальный выигрыш (проигрыш) на всех последующих шагах был бы максимальным (минимальным). На основе принципа оптимальности Беллмана строится схема решения монгошаговой задачи, состоящая из 2-х частей:

1) Обратный ход:от последнего шага к первому получают множество возможных оптимальных («условно-оптимальных») управлений.

2) Прямой ход:от известного начального состояния к последнему из полученного множества «условно-оптимальных» управлений составляется искомое оптимальное управление для всего процесса в целом.

Оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на n-м шаге, затем на двух последних шагах, затем на трех последних шагах и т.д., вплоть до первого шага.

Чтобы можно было использовать принцип оптимальности практически, необходимо записать его математически. Обозначим через z₁(x_n-1),z₂(x_n-2),…,z_n(x₀) условно-оптимальные значения приращений целевой функции на последнем шаге, двух последних,…, на всей последовательности шагов, соответственно.

Тогда для последнего шага:

z₁(x_n-1) =(min) n(x_n-1,u_n)>,

где u_n– множество допустимых (возможных) управлений наn-ом шаге,x_n-1– возможные состояния системы передn-ым шагом.

Для двух последних шагов:

z₂(x_n-2) =(min) n_-1(x_n-2,u_n-1) +z₁(x_n-1)>.

Для k последних шагов:

z_k(x_n-k) = (min) n-k+1(x_n-k, u_n-k+1) + z_k-1(x_n-k+1)>.

Для всех n шагов:

z_n(x₀) = (min) 1(x₀, u₁) + z_n-1(x₁)>.

Полученные рекуррентные соотношения называют функциональными уравнениями Беллмана.

При этом согласно определению z_n(x₀) =F*.

Источник

1.7. Метод динамического программирования

Метод динамического программирования (ДП) 1 был предложен известным математиком Р.Беллманом как очень общий подход к решению некоторых типов задач из разных областей дискретной и непрерывной математики, включая даже вариационное исчисление. В данном пособии будет рассматриваться только приложение этого метода к комбинаторным задачам.

Рассмотренный выше метод ветвей и границ является попыткой ограничить перебор при движении по дереву сверху вниз. Метод ДП действует в какой-то мере противоположным образом.

Вспомним дерево перебора, изображенное на рис.1.1. Если корень дерева представляет исходную задачу, то с каждой вершиной обычно можно связать некоторую подзадачу того же типа, но меньшей размерности. Например, вершины на один уровень ниже корня являются корневыми для поддеревьев перебора, решающих задачи с различными фиксированными значениями x₁. Листья дерева в таком случае представляют простейшие задачи, решение которых получается сразу, без перебора. В ходе решения исходной задачи выполняется решение всех подзадач. Как мы знаем, основной недостаток решения задач путем полного перебора заключается в астрономически большом количестве решаемых подзадач.

Для некоторых практически важных задач дерево перебора обладает приятным свойством: многие вершины, лежащие на разных ветвях дерева, соответствуют одинаковым подзадачам, т.е. соответствующие поддеревья абсолютно одинаковы. Это наводит на мысль, что нет смысла много раз решать одни и те же подзадачи. Следует найти такой способ организации исчерпывающего перебора, при котором каждая подзадача решается один раз, а результат ее решения может использоваться многократно.

Примером ситуации, описанной в предыдущем абзаце, может служить решение задачи о рюкзаке. Допустим, нужно уложить рюкзак объемом 100 единиц, и при этом уже найдена оптимальная укладка для рюкзака объемом 20 единиц. Далее можно пытаться по-разному распорядиться остальными 80 единицами, всякий раз используя готовое решение для 20. В свою очередь, при решении задачи для объема 20 единиц может многократно понадобиться распорядиться меньшим объемом, например, 10 единицами, и если эта подзадача была заранее решена, то ее результат очень пригодится.

Другой пример – задача о коммивояжере. Допустим, мы рассмотрели все варианты проезда из города Aв городBс заездом вC,DиE:ACDEB,ADECB,AEDCBи т.п. При этом найден кратчайший из таких путей. Далее в ходе отыскания полного маршрута можно использовать этот результат всякий раз, когда будет рассматриваться маршрут изBвA, проходящий через все города, кромеC,DиE.

Решение комбинаторной задачи методом ДП выглядит следующим образом:

Источник

Рекурсия и динамическое программирование

Что можно сделать с функцией. Синтаксис описания функции в Си. Синхронные и асинхронные вызовы. Адрес возврата и стек вызовов. Пример отладки программы с наблюдением за Call stack. Локальные переменные и параметры хранятся на стеке.

functions.c

#include void A(); void B(); void C(); int main(int argc, char* argv[])  printf("main() called.\n"); A(); printf("main() returns.\n"); return 0; > void A()  printf(" A() called.\n"); B(); printf(" A() returns.\n"); > void B()  printf(" B() called.\n"); C(); printf(" B() returns.\n"); > void C()  printf(" C() called.\n"); printf(" C() returns.\n"); > 

Рекурсия. Репка и матрёшка

Сказка «Репка». Крайний случай. Прямой и обратный ход рекурсии. Алгоритм изготовления матрёшки. Программа, печатающая матрёшку.

matryoshka.c

#include void matryoshka(int n); int main(int argc, char* argv[])  matryoshka(7); return 0; > void matryoshka(int n)  if (n == 1) printf(" Last matryoshka. %d\n", n); else  printf(" Top side of matryoshka %d\n", n); matryoshka(n-1); printf(" Bottom side of matryoshka %d\n", n); > > 

Примеры рекурсивных алгоритмов

Факториал числа. Алгоритм Евклида. Быстрое возведение в степень. Числа Фибоначчи.

recursion_examples.c

#include int factorial(int n)  if (0 == n) return 1; return factorial(n-1)*n; > int gcd(int a, int b)  if (0 == b) return a; return gcd(b, a%b); > double fast_power(double a, int n)  if (0 == n) return 1; if (n%2 == 1) return a*fast_power(a, n-1); else return fast_power(a*a, n/2); > int fib(int n)  if (n  1) return n; else return fib(n-1) + fib(n-2); > int main(int argc, char* argv[])  int n, m; scanf("%d%d", &n, &m); printf("factorial(%d) = %d\n", n, factorial(n)); printf("gcd(%d, %d) = %d\n", n, m, gcd(n, m)); printf("fast_power(%d, %d) = %lf\n", n, m, fast_power(n, m)); printf("fib(%d) = %d\n", n, fib(n)); return 0; > 

Ханойские башни

Постановка задачи. Рекуррентный алгоритм и его реализация.

hanoi.c

#include void hanoi(int n, int i, int k); int main(int argc, char* argv[])  hanoi(3, 1, 2); return 0; > void hanoi(int n, int i, int k)  if (n == 1) printf("Move disk 1 from pin %d to %d.\n", i, k); else  int tmp = 6 - i - k; hanoi(n-1, i, tmp); printf("Move disk %d from pin %d to %d.\n", n, i, k); hanoi(n-1, tmp, k); > > 

Динамическое программирование сверху и снизу

Скорость рекуррентного вычисления чисел Фибоначчи. Проблема повторных вычислений. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений Динамическое программирование сверху и снизу.

fibonacci_time.c

#include #include static int cache[100] = 0>; int fib(int n)  if (n  1) return n; if (cache[n] == 0) cache[n] = fib(n-1) + fib(n-2); return cache[n]; > int fib_dynamic(int n)  int Fib[n+1]; Fib[0] = 0; Fib[1] = 1; for (int i = 2; i  n; ++i) Fib[i] = Fib[i-1] + Fib[i-2]; return Fib[n]; > int main(int argc, char* argv[])  for (int n = 1; n  50; n += 1)  clock_t time1 = clock(); int result = fib_dynamic(n); clock_t time2 = clock(); int delta_ms = (time2 - time1)*1000/CLOCKS_PER_SEC; printf("fib(%d) = %d,\t time = %d ms\n", n, result, delta_ms); > return 0; > 

Динамическое программирование: траектории кузнечика

Задача из ЕГЭ про граф дорог. Количество различных траекторий кузнечика из 1 в N. Реализация динамическим программированием.

grasshopper.c

#include int number_of_trajectories(int n)  int K[n+1]; K[0] = 0; K[1] = 1; for (int i = 2; i  n; ++i) K[i] = K[i-1] + K[i-2]; return K[n]; > int main(int argc, char* argv[])  int finish; scanf("%d", &finish); printf("Grasshopper has %d trajectories from 1 to %d\n", number_of_trajectories(finish), finish); return 0; > 

Самостоятельная работа

К 4-му уроку есть домашняя работа в форме контеста: ссылка на ДЗ №4. Ссылка на неё также находится на главной странице сайта.

Если у вас нет логина и пароля, зарегистрируйтесь на 1-й контест, и доступ к остальным вы получите автоматически.

Сайт построен с использованием Pelican. За основу оформления взята тема от Smashing Magazine. Исходные тексты программ, приведённые на этом сайте, распространяются под лицензией GPLv3, все остальные материалы сайта распространяются под лицензией CC-BY.

Источник