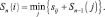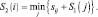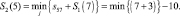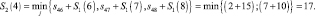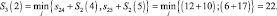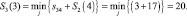Научная электронная библиотека
В предыдущих разделах были рассмотрены одношаговые или одноэтапные методы оптимизации. Теперь перейдем к многошаговым методам оптимизации. Одним из наиболее известных многошаговых методов оптимизации является динамическое программирование, предложенное в пятидесятые годы прошлого века американским ученым Ричардом Беллманом. Динамическое программирование можно определить, как набор математических процедур, используемых при анализе многошаговых процессов принятия решений [17]. В свою очередь многошаговый процесс принятия решений можно определить, как деятельность, при которой принимаются последовательные решения, направленные на достижение единой цели.
Суть динамического программирования заложено в принципе оптимальности, которая звучит так – оптимальная стратегия обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальную стратегию относительно состояния, возникающего после первого решения [3].
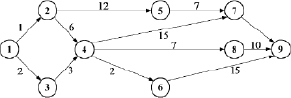
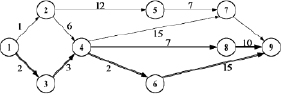
Многошаговые процессы принятия решений встречаются в самых различных ситуациях, например, в задачах управления запасами, при распределении ресурсов или управлении космическим аппаратом. Каждый многошаговый процесс принятия решений интуитивно можно считать, как развитием наиболее понятного многошагового процесса нахождения кратчайшего пути в направленной сети (рис. 6.1). На этом примере можно наиболее наглядно продемонстрировать и суть самого принципа оптимальности Р. Беллмана.
Пусть направленная сеть имеет N этапов принятия решений. Из визуального анализа сети, изображенной на рис. 6.1 можно принять N = 5. Введем следующие обозначения:
n – номер этапа (n = 1, 2, 3, 4,5 );
i – пункт, откуда осуществляется движение (i = 1, 2, …, 8);
j – пункт, в который направлено движение (j = 2, 3, …, 9);
sij – расстояние из пункта i в пункт j;
Sn(i) – минимальное расстояние на n-м этапе решения задачи из пункта i до конечного пункта.
Будем считать, что пункт принадлежит n-му этапу, если из него можно попасть в конечный пункт ровно за n этапов.
Очевидно, что минимальный путь из пункта n-го этапа до конечного пункта 9 будет зависеть от того, в каком пункте этого этапа мы окажемся. Номер i пункта, принадлежащего n-му этапу, будет являться переменной состояния системы на n-м этапе. Поскольку оптимизация обычно начинается с конца процесса, то, находясь в некотором пункте i n-го этапа, принимается решение о переходе в один из пунктов (n – 1)-го этапа, а направление дальнейшего движения известно из предыдущих этапов. Номер j пункта (n – 1)-го этапа будет переменной управления на n-м этапе.
Для первого этапа (n = 1) целевая функция (функция Беллмана) представляет собой минимальный путь из пунктов первого этапа (6, 7, 8) в конечный пункт 9, т.е. S1(i) = si9. Для последующих этапов длина пути складываются из двух слагаемых – пути sij из пункта i n-го этапа в пункт j (n – 1)-го этапа и минимально возможной длины пути из пункта j до конечного пункта, т.е. Sn–1(j). Таким образом, функциональное уравнение Беллмана будет иметь вид
Минимальная длина достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт.
На пятом этапе попадаем на исходный пункт и состояние системы становится определенным i = 1. Функция S5(1) представляет собой минимально возможный путь из 1-го пункта в 9-й пункт. Оптимальный маршрут определяется в результате анализа всех этапов в обратном порядке.
Проиллюстрируем этот пример по конкретным значениям длин дуг, показанных на рис. 6.1.
Пример 6.1. Алгоритм определения кратчайшего пути состоит из следующих шагов.
Шаг 1. n = 1, S1(i) = si9. На первом этапе в пункт 9 можно попасть из пунктов 6, 7, 8 второго этапа. Следовательно: S1(6) = 15; S1(7) = 3; S1(8) = 10.
Шаг 2. n = 2, здесь рассматриваем пути из пунктов (4 и 5) третьего этапа в пункты второго этапа. Функциональное уравнение Беллмана здесь имеет вид:
Условно оптимальный путь (5–7);
Условно оптимальные пути (4–6 и 4–8).
Шаг 3. n = 3, здесь рассматриваем пути из пунктов (2 и 3) четвертого этапа в пункты третьего этапа.
Условно оптимальный путь (2–5).
Условно оптимальный путь (3–4).
Шаг 4. n = 4, здесь рассматриваем пути из начального пункта 1 в пункты четвертого этапа.
Условно оптимальный путь (1–3).
Теперь найдем безусловный кратчайший путь от пункта 1 до пункта 9. На этапе условной оптимизации получено, что минимальный путь имеет длину S4(1) = 22. Этот результат достигается при движении из первого пункта в третий, затем необходимо двигаться в четвертый. Из этого пункта, как показано на шаге 2 возможно два равнозначных направления в пункты 6 и 7. Таким образом, оптимальное решение достигается двумя маршрутами, показанными на рис. 6.2, а именно (1–3–4–6–9) и (1–3–4–8–9).
Лекции_1 / Лекция 9. Введение в ДП. Принцип оптимальности Беллмана
Введение в динамическое программирование. Многошаговые процессы принятия решений. Принцип оптимальности Р. Беллмана.
Понятие о динамическом программировании.
ДП (планирование) представляет собой математический метод для нахождения оптимальных решений многошаговых (многоэтапных) задач. Некоторые из таких задач естественным образом распадаются на отдельные шаги (этапы), но имеются задачи, в которых разбиение приходится вводить искусственно, для того чтобы их можно было решить методом ДП.
Обычно методами ДП оптимизируют работу некоторых управляемых систем, эффект которой оценивается аддитивной, или мультипликативной, целевой функцией. Аддитивной называется такая функция нескольких переменных 
, значение которой вычисляется как сумма некоторых функций 
, зависящих только от одной переменной 
: 
. Слагаемые аддитивной целевой функции соответствуют эффекту решений, принимаемых на отдельных этапах управляемого процесса.
Принцип оптимальности Р. Беллмана.
Смысл подхода, реализуемого в динамическом программировании, заключен в замене решения исходной многомерной задачи последовательностью задач меньшей размерности. Основные требования к задачам:
1. объектом исследования должна служить управляемая система (объект) с заданными допустимыми состояниями и допустимыми управлениями;
2. задача должна позволять интерпретацию как многошаговый процесс, каждый шаг которого состоит из принятия решения о выборе одного из допустимых управлений, приводящих к изменению состояния системы;
3. задача не должна зависеть от количества шагов и быть определенной на каждом из них;
4. состояние системы на каждом шаге должно описываться одинаковым (по составу) набором параметров;
5. последующее состояние, в котором оказывается система после выбора решения на k-м шаге, зависит только от данного решения и исходного состояния к началу k—го шага. Данное свойство является основным с точки зрения идеологии динамического программирования и называется отсутствием последствия.
Рассмотрим вопросы применения модели динамического программирования в обобщенном виде. Пусть стоит задача управления некоторым абстрактным объектом, который может пребывать в различных состояниях. Текущее состояние объекта отождествится с некоторым набором параметров, который обозначается в дальнейшем 
и называется вектором состояния. Предполагается, что задано множество 
всех возможных состояний. Для объекта определено также множество допустимых управлений (управляющих воздействий) X, которое, не умаляя общности, можно считать числовым множеством. Управляющие воздействия могут осуществляться в дискретные моменты времени 
, причем управленческое решение заключается в выборе одного из управлений 
. Планом задачи или стратегией управления называется вектор 
, компонентами которого служат управления, выбранные на каждом шаге процесса. Ввиду предполагаемого отсутствия последействия между каждыми двумя последовательными состояниями объекта 
и 
, существует известная функциональная зависимость, включающая также выбранное управление: 
. Тем самым задание начального состояния объекта 
и выбор плана х однозначно определяют траекторию поведения объекта.
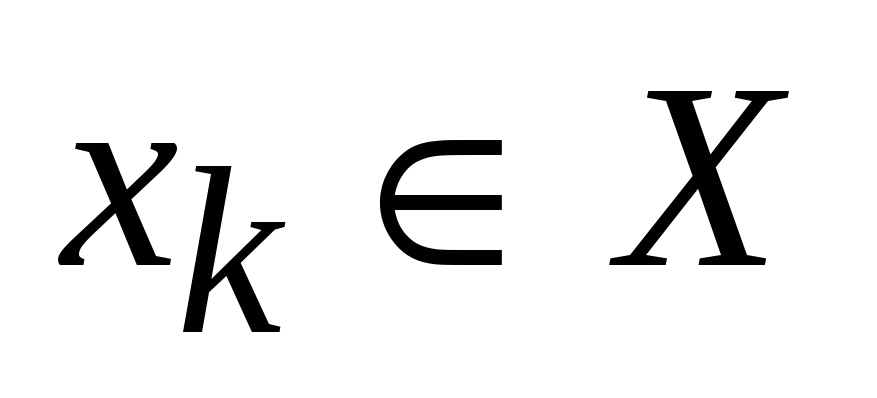
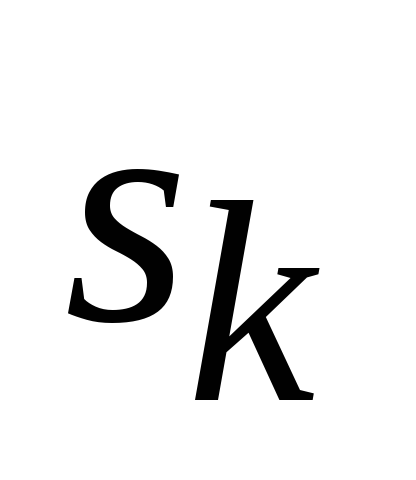
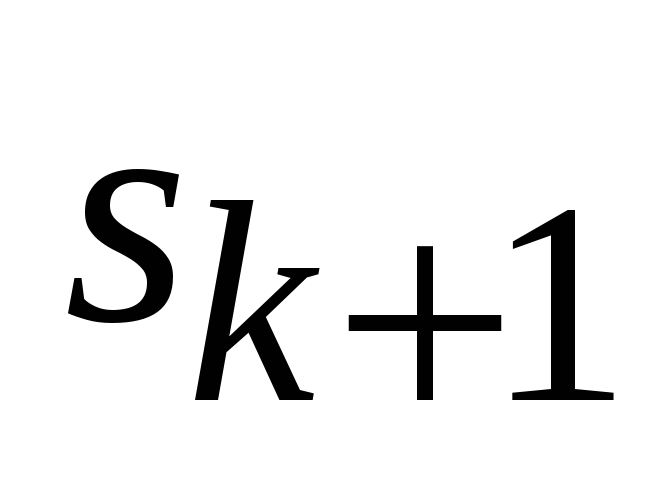
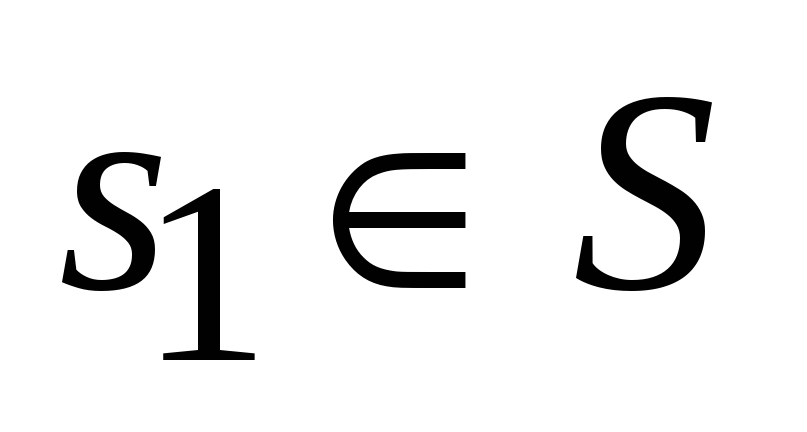
Эффективность управления на каждом шаге k зависит от текущего состояния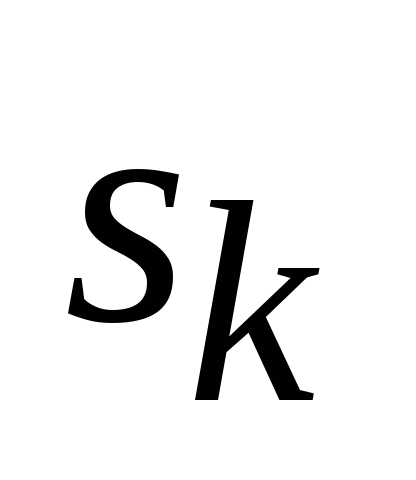 
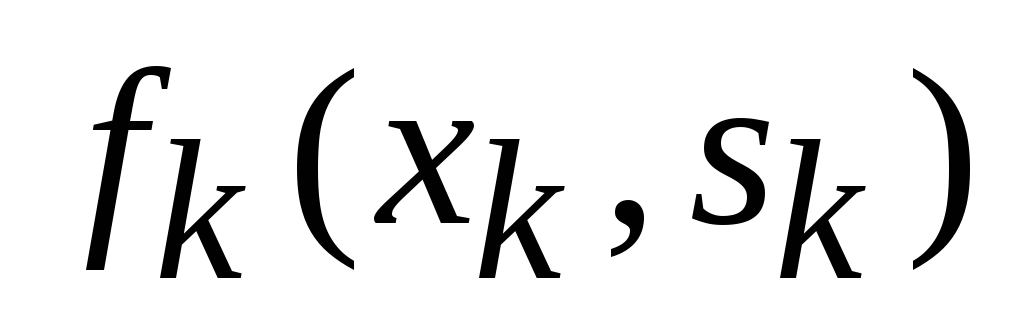
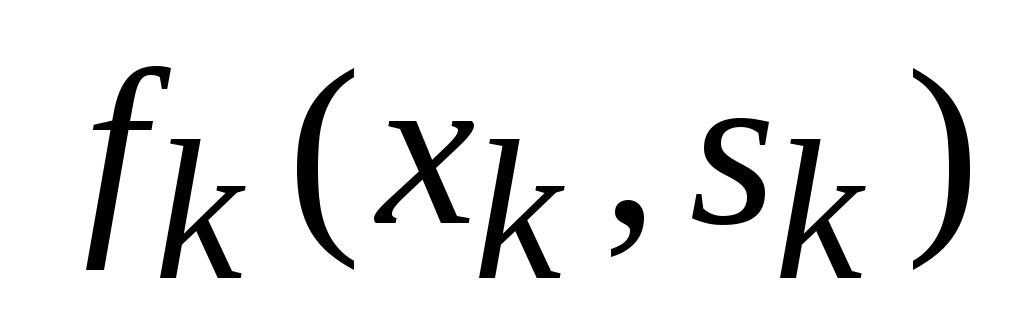
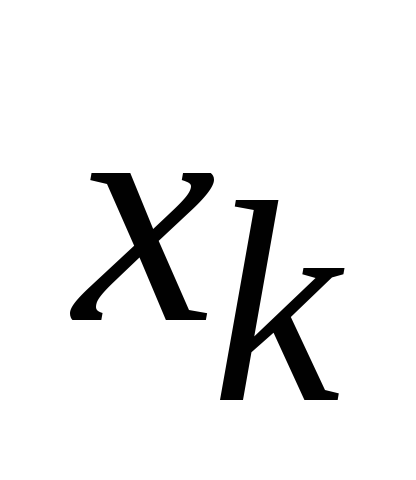
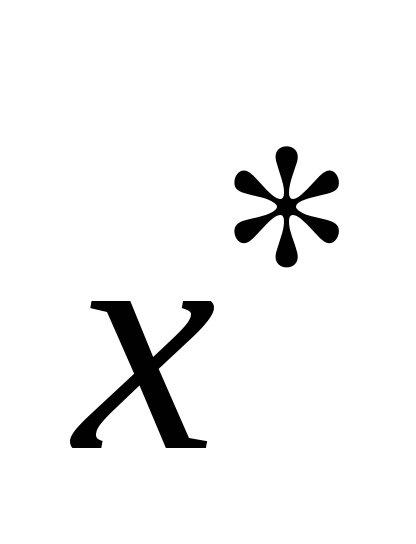
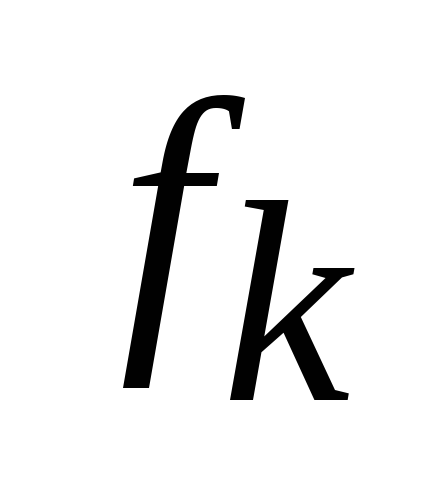
, выбранного управления 
и количественно оценивается с помощью функций 
, являющихся слагаемыми аддитивной целевой функции, характеризующей общую эффективность управления объектом. (Отметим, что в определение функции 
включается область допустимых значений 
, и эта область, как правило, зависит от текущего состояния 
). Оптимальное управление, при заданном начальном состоянии 
, сводится к выбору такого оптимального плана 
, при котором достигается максимум суммы значений 
на соответствующей траектории.
Основной принцип динамического программирования заключается в том, что на каждом шаге следует стремиться не к изолированной оптимизации функции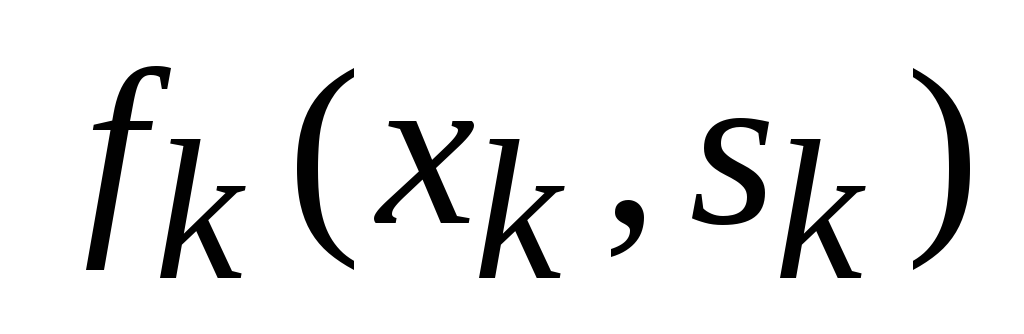 
, а выбирать оптимальное управление 
в предположении об оптимальности всех последующих шагов. Формально указанный принцип реализуется путем отыскания на каждом шаге k условных оптимальных управлений 
, обеспечивающих наибольшую суммарную эффективность начиная с этого шага, в предположении, что текущим является состояние 
.
Обозначим 
максимальное значение суммы функций 
на протяжении шагов от k до п (получаемое при оптимальном управлении на данном отрезке процесса), при условии, что объект в начале шага k находится в состоянии 
. Тогда функции 
должны удовлетворять рекуррентному соотношению:
(*), где 
.
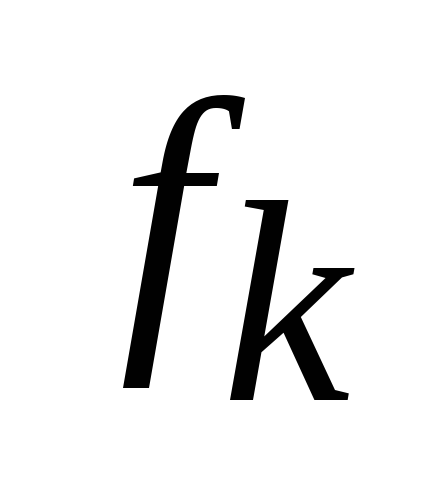
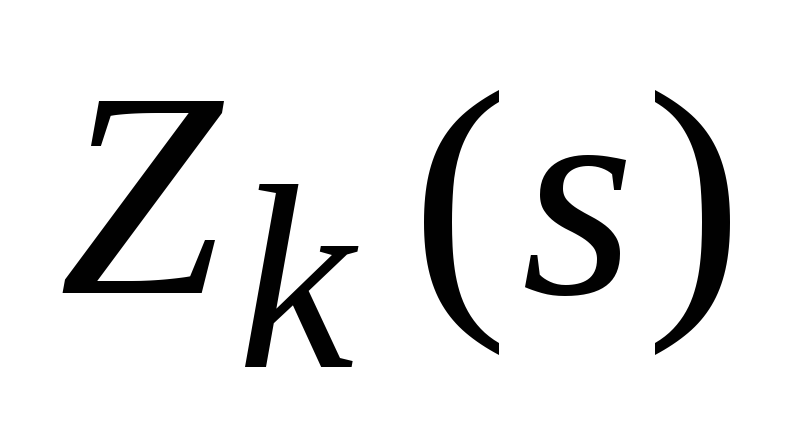
Это соотношение называют основным рекуррентным соотношением (основным функциональным уравнением) динамического программирования. Оно реализует базовый принцип динамического программирования, известный также как принцип оптимальности Беллмана:
Оптимальная стратегия управления должна удовлетворять следующему условию: каково бы ни было начальное состояние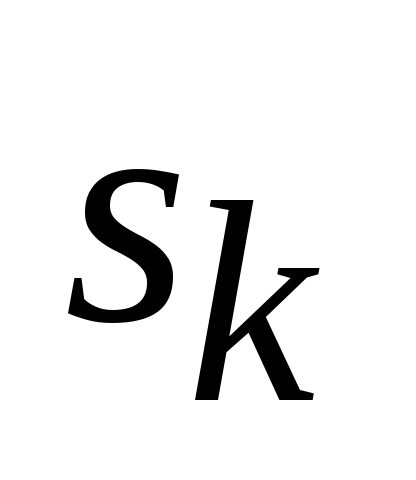 
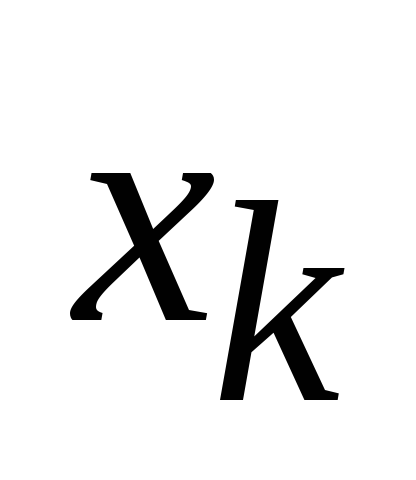
на k-м шаге и выбранное на этом шаге управление 
, последующие управления (управленческие решения) должны быть оптимальными по отношению к cocmoянию 
, получающемуся в результате решения, принятого на шаге k.
Основное соотношение позволяет найти функции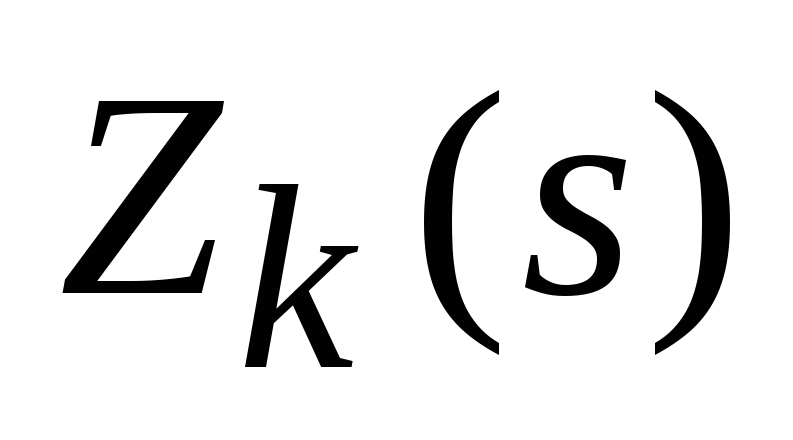 
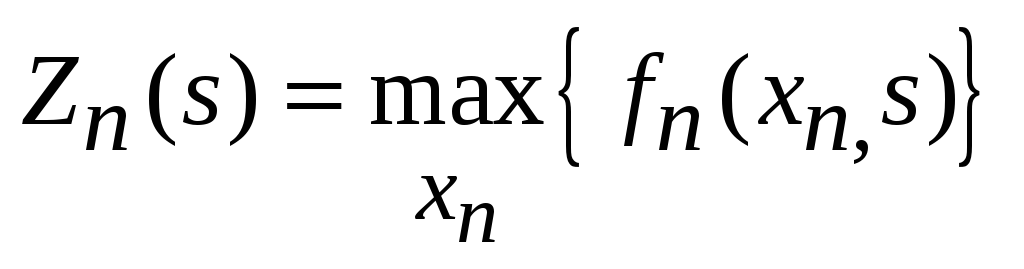
только в сочетании с начальным условием, каковым в нашем случае является равенство 
.
Сформулированный выше принцип оптимальности применим только для управления объектами, у которых выбор оптимального управления не зависит от предыстории управляемого процесса, т. е. от того, каким путем система пришла в текущее состояние. Именно это обстоятельство позволяет осуществить декомпозицию задачи и сделать возможным ее практическое решение.
Для каждой конкретной задачи функциональное уравнение имеет свой специфический вид, но в нем непременно должен сохраняться рекуррентный характер, заложенный в выражении (*) и воплощающий основную идею принципа оптимальности.