Динамическое программирование числа фибоначчи python

Практика: Динамическое программирование

Динамическое программирование — решение сложной задачи разбиением её на более простые подзадачи, при этом каждая подзадача решается только один раз.

Динамическое программирование очень похоже на рекурсию, при этом:

• динамическое программирование сверху — это по сути рекурсия с кешированием;
• динамическое программирование снизу — это переформулирование задачи в виде индуктивной последовательности подзадач, от крайнего случая к более сложным.

Одномерное динамическое программирование

Классическая задача — числа Фибоначчи

Последовательность Фибоначчи Fn задается формулами: F1 = 1, F2 = 1, Fn = Fn – 1 + Fn – 2 при n > 1. Необходимо найти Fn по номеру n.

Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:

def fib(n): if n  1: return n else: return fib(n-1) + fib(n-2) 

Используя такую функцию, мы будем решать задачу «с конца» — будем шаг за шагом уменьшать n, пока не дойдем до известных значений.

Но как можно заметить, такая, казалось бы, простая программа уже при n = 40 работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.

Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования (кеширование):

F = [-1]*MAX_POSSIBLE_N def fib(n): if n  1: return n if F[n] == -1: F[n] = fib(n-1) + fib(n-2) return F[n] 

Приведенное решение корректно и эффективно. Но можно поступить ещё проще:

def fib(n): F = [-1]*(n+1) F[0] = 0 F[1] = 1 for i in range(2, n+1): F[i] = F[i - 1] + F[i - 2] return F[n] 

Такое решение можно назвать решением «с начала» — мы первым делом заполняем известные значения, затем находим первое неизвестное значение, потом следующее и т.д., пока не дойдем до нужного.

Именно такое решение и является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все F[i] для i < n), затем, зная решения подзадач, нашли ответ.

Задача о кузнечике — количество способов

Рассмотрим следующую задачу. На числовой прямой сидит кузнечик, который может прыгать вправо на одну или на две единицы. Первоначально кузнечик находится в точке с координатой 1. Определите количество различных маршрутов кузнечика, приводящих его в точку с координатой n.

Обозначим количество маршрутов кузнечика, ведущих в точку с координатой n, как K[n]. Прежде всего заметим, что существует ровно один маршрут из точки 1 в точку 1 — он не содержит ни одного прыжка. В точку 2 можно прыгнуть единственным способом — из точки 1.

Как вычислить K[n]? В точку кузнечик может попасть двумя способами — из точки при помощи прыжка длиной 2 и из точки прыжком длины 1. То есть число способов попасть в точку n равно сумме числа способов попасть в точку (n-1) и (n-2), что позволяет выписать рекуррентное соотношение: K[n] = K[n-1] + K[n-2] .

Можно заметить, что данная задача по сути свелась к числам Фибоначчи, поэтому мы не будем выписывать её решение.

Упражнение №1

Решите задачу о количестве способов достичь точки n из точки 1, если кузнечик умеет прыгать +1, +2 и +3.

Упражнение №2

Решите задачу о количестве способов достичь точки n из точки 1, если кузнечик умеет прыгать +1, +2 и *3.

Задача о кузнечике со стоимостями посещения точек

Пусть кузнечик прыгает на одну или две точки вперед, а за прыжок в каждую точку необходимо заплатить определенную стоимость, различную для различных точек. Стоимость прыжка в точку i задается значением price[i] списка price. Необходимо найти минимальную стоимость маршрута кузнечика из точки 0 в точку n.

На этот раз нам необходимо модифицировать определение целевой функции. Пусть C[n] — минимальная стоимость пути из 1 в n.

Выведем рекуррентное соотношение для этой функции.Чтобы попасть в точку n мы должны попасть в неё последним прыжком из (n-1) или (n-2). Минимальные стоимости этих маршрутов будут равны С[n-1] и С[n-2] соответственно, к ним придется добавить значение price[n] за прыжок в клетку n. Но из двух клеток мы можем выбрать любую.

Нужно выбрать тот маршрут, который имеет наименьшую стоимость: C[n] = min(C[n-1], C[n-2]) + price[n]

Вычислить значение целевой функции также лучше при помощи динамического программирования, а не рекурсии.

Упражнение №3

Напишите функцию calculate_min_cost(n, price) вычисления наименьшей стоимость достижения клетки n из клетки 1

Восстановление наиболее выгодной траектории

Итак, мы нашли список С, где будет записана минимальная стоимость маршрута для всех точек от 1 до n.

Но помимо нахождения наименьшей стоимости маршрута, разумеется, хотелось бы найти и сам маршрут минимальной стоимости. Такая задача называется задачей «восстановления ответа».

Для восстановления ответа будем для каждой точки запоминать номер точки prev[i], из которой кузнечик попал в точку i, если он будет передвигаться по пути минимальной стоимости. То есть prev[i] — это точка, предшествующая точке с номером i на пути минимальной стоимости (также говорят, что Prev — это массив предшественников). Как определить prev[i]? Если C[i-1] < C[i-2] , то кузнечик попал в точку i из точки (i-1), поэтому prev[i] = i - 1, иначе prev[i] = i - 2.

Для восстановления пути необходимо начать с точки n и переходить от каждой точки к ее предшественнику, пока путь не дойдет до начальной точки с номером 0. Номера всех вершин будем добавлять в список path. В конце в список path добавляется начальная вершина номер 1, которая не была обработана в основном цикле, а затем весь список path разворачивается в обратном порядке (т. к. вершины добавляются в обратном порядке, от конечной к начальной).

Упражнение №4

Модифицируйте алгоритм вычисления значений целевой функции так, чтобы вычислить значения prev[i], и восстановите траекторию наименьшей стоимости из точки 1 в точку n.

Двумерное динамическое программирование

Игра с ферзём

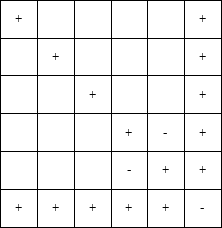
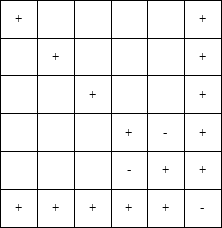
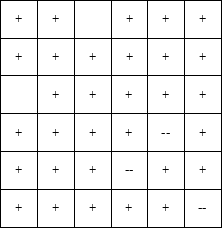
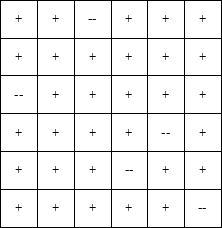
Рассмотрим игру «Ферзя в угол» для двух игроков. В левом верхнем углу доски размером N*M находится ферзь, который может двигаться только вправо-вниз. Игроки по очереди двигают ферзя, то есть за один ход игрок может переместить ферзя либо по вертикали вниз, либо по горизонтали вправо, либо во диагонали вправо-вниз. Выигрывает игрок, который поставит ферзя в правый нижний угол. Необходимо определить, какой из игроков может выиграть в этой игре независимо от ходов другого игрока (имеет выигрышную стратегию).

Будем заполнять доску знаками «+» и «-». Знак «+» будет означать, что данная клетка является выигрышной для ходящего с неё игрока (то есть если ферзь стоит в этой клетке, то игрок, который делает ход, может всегда выиграть), а знак «-» означает, что он проигрывает. Клетки последней строки, последнего столбца и диагонали, ведущей из правого нижнего угла необходимо отметить, как «+», так как если ферзь стоит в этой клетке, то ходящий игрок может выиграть одним ходом.

Но в правом нижнем углу необходимо поставить знак «-» — если ферзь стоит в углу, то тот игрок, которых должен делать ход, уже проиграл.

Теперь рассмотрим две клетки, из которых можно пойти только в те клетки, в которых записан знак «+». В этих клетках нужно записать знак «-» — если ферзь стоит в этих клетках, то какой бы ход не сделал ходящий игрок, ферзь окажется в клетке, в которой стоит знак «+», то есть выигрывает ходящий игрок. Значит, тот, кто сейчас ходит — всегда проигрывает.

Но теперь в те клетки, из которых можно попасть в клетку, в которой стоит знак «-» за один ход, необходимо записать знак «+» — если ферзь стоит в этой клетке, то игрок, который делает ход, может выиграть, если передвинет ферзя в клетку, в которой стоит знак «-»:

Дальше таблица заполняется аналогично. В клетке ставиться знак «+», если есть ход, который ведет в клетку, в которой стоит знак «--». В клетке ставится знак «-», если все ходы из этой клетки ведут в клетки, в которых записан знак «+».

Продолжая таким образом, можно определить выигрывающего игрока для любой начальной клетки.

Упражнение №5

Реализовать алгоритм поиска выигрышных и проигрышных позиций в игре с ферзём на прямоугольном поле M на N, где N — высота, а M — ширина поля.

Упражнение №6

Реализовать алгоритм поиска выигрышных и проигрышных позиций в аналогичной игре, но ходы делает король (только вправо, вниз и по диагонали).

Сайт построен с использованием Pelican. За основу оформления взята тема от Smashing Magazine. Исходные тексты программ, приведённые на этом сайте, распространяются под лицензией GPLv3, все остальные материалы сайта распространяются под лицензией CC-BY-SA.

Источник

Числа Фибоначчи: циклом и рекурсией

Числа Фибоначчи – это ряд чисел, в котором каждое следующее число равно сумме двух предыдущих.

Иногда ряд начинают с нуля.

В данном случае мы будем придерживаться первого варианта.

Вычисление n-го числа ряда Фибоначчи с помощью цикла while

Присвоим переменным fib1 и fib2 значения двух первых элементов ряда, то есть единицы.

Получим от пользователя номер элемента, значение которого требуется вычислить. Присвоим номер элемента переменной n .

Поскольку значения первых двух элементов ряда Фибоначчи нам уже известны и вычисления начинаем с третьего, количество проходов по телу цикла должно быть на 2 меньше значения n , то есть n - 2 .

Если пользователь вводит 1 или 2, тело цикла ни разу не выполняется, на экран выводится исходное значение fib2 .

1. Сложить fib1 и fib2 , присвоив результат переменной для временного хранения данных, например, fib_sum .
2. Переменной fib1 присвоить значение fib2 .
3. Переменной fib2 присвоить значение fib_sum .

После окончания работы цикла вывести значение fib2 на экран.

fib1 = 1 fib2 = 1 n = input("Номер элемента ряда Фибоначчи: ") n = int(n) i = 0 while i  n - 2: fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print("Значение этого элемента:", fib2)

Пример выполнения программы:

Номер элемента ряда Фибоначчи: 10 Значение этого элемента: 55

fib1 = fib2 = 1 n = input("Номер элемента ряда Фибоначчи: ") n = int(n) - 2 while n > 0: fib1, fib2 = fib2, fib1 + fib2 n -= 1 print("Значение этого элемента:", fib2)

Вывод ряда чисел Фибоначчи с помощью цикла for

В данном случае выводится не только значение искомого элемента ряда Фибоначчи, но и все числа до него включительно. Для этого вывод значения fib2 помещен в цикл.

fib1 = fib2 = 1 n = int(input()) print(fib1, fib2, end=' ') for i in range(2, n): fib1, fib2 = fib2, fib1 + fib2 print(fib2, end=' ') 

10 1 1 2 3 5 8 13 21 34 55

Рекурсивное вычисление n-го числа ряда Фибоначчи

1. Если n = 1 или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
2. Во всех остальных случаях вызвать эту же функцию с аргументами n - 1 и n - 2. Результат двух вызовов сложить и вернуть в вызывающую ветку программы.

def fibonacci(n): if n in (1, 2): return 1 return fibonacci(n - 1) + fibonacci(n - 2) print(fibonacci(10))

Допустим, n = 4. Тогда произойдет рекурсивный вызов fibonacci(3) и fibonacci(2). Второй вернет единицу, а первый приведет к еще двум вызовам функции: fibonacci(2) и fibonacci(1). Оба вызова вернут единицу, в сумме будет два. Таким образом, вызов fibonacci(3) возвращает число 2, которое суммируется с числом 1 от вызова fibonacci(2). Результат 3 возвращается в основную ветку программы. Четвертый элемент ряда Фибоначчи равен трем: 1 1 2 3.

Источник