Деление больших чисел python

Деление больших чисел в Python

Но это дает мне результат -1.481136900397802034028076389E+280 Я предполагаю, что я не говорю python, как правильно обрабатывать большие числа, но я в тупике от того, куда идти отсюда. Я также должен добавить, что конечной целью является вычисление

6 ответов

Развернув мой комментарий, если N и f2 long строго больше 0, то

точно ceil(N / float(f2)) (но еще точнее, чем использование float).

(Использование // вместо / для целочисленного деления для совместимости с Python 3.x не требует дополнительных усилий.)

Это потому, что N // f2 дает вам (в основном) floor(N / float(f2)) , и поэтому N // f2 + 1 почти всегда совпадает с ceil . Однако, когда N является кратным f2 , N // f2 + 1 слишком велико ( +1 не должно быть там), но с помощью N — 1 исправляет это и не нарушает другой случай.

(Это не работает ни для N , f2 меньше или равно 0, но может обрабатываться отдельно)

fmin является float после того, как вы разделите длинное целое число на float. Его значение 1.84952718165824e+305 . Добавление 1 к этому не меняет его вообще, точность просто не такая высокая.

Если вы выполняете целочисленное деление, fmin остается long :

>>> fmin = N / f2 >>> fmin 18495271816582402193321106509793602189617847415669131056768139225220221855498293 49983070478076000952025038039460539798061570960870927236986153971731443029057201 52035339202255934728764897424408896865977423536890485615063959262845076766281553 766072964756078264853041334880929452289298495368916583660903481130L >>> N - (fmin * f2) 111L 

Конечно, вы не получаете 0 из-за целочисленного деления, в котором десятичная часть результата отбрасывается. Но теперь добавление 1 будет иметь значение:

Использование модуля Decimal не изменяет проблему:

>>> from decimal import Decimal, getcontext >>> fmin = Decimal(N) / Decimal(f2) >>> fmin Decimal('1.849527181658240219332110651E+305') 

По-прежнему нет неограниченной точности, и даже если вы установите Decimal.getcontext().prec = 2000 , вы все равно не получите ровно 0.

Источник

Как в Python реализованы очень длинные числа типа integer?

Когда вы пишете на низкоуровневом языке, таком как С, вы беспокоитесь о выборе правильного типа данных и спецификаторах для ваших целых чисел, на каждом шаге анализируете достаточно ли будет использовать просто int или нужно добавить long или даже long double . Однако при написании кода на Python вам не нужно беспокоиться об этих «незначительных» вещах, потому что Python может работать с числами типа integer любого размера.

В С, если вы попытаетесь вычислить 2 20000 с помощью встроенной функции powl , то на выходе получите inf .

#include #include int main(void) < printf("%Lf\n", powl(2, 20000)); return 0; >$ ./a.out inf

Но в Python сделать это проще простого:

>>> 2 ** 20000 39802768403379665923543072061912024537047727804924259387134 . . . 6021 digits long . . 6309376

Должно быть под капотом Python делает что-то очень красивое и сегодня мы узнаем, что именно он делает, чтобы работать с целыми числами произвольного размера!

Представление и определение

Integer в Python это структура C, определенная следующим образом:

PyObject_VAR_HEAD – это макрос, он раскрывается в PyVarObject , который имеет следующую структуру:

typedef struct < PyObject ob_base; Py_ssize_t ob_size; /* Number of items in variable part */ >PyVarObject;

Другие типы, у которых есть PyObject_VAR_HEAD :

В структуре PyObject есть некоторые мета-поля, используемые для подсчета ссылок (сборки мусора), но для того, чтобы поговорить об этом нужна отдельная статья. Поле, на котором мы сосредоточимся это ob_digit и в немного ob_size .

Расшифровка ob_digit

ob_digit – это статически аллоцированый массив единичной длины типа digit (typedef для uint32_t) . Поскольку это массив, ob_digit в первую очередь является указателем на число, и, следовательно, при необходимости он может быть увеличен с помощью функции malloc до любой длины. Таким образом python может представлять и обрабатывать очень длинные числа.

Как правило в низкоуровневых языках, таких как С, точность целых чисел ограничена 64-битами, однако Python поддерживает целые числа произвольной точности. Начиная с версии Python 3, все числа представлены в виде bignum и ограничены только доступной памятью системы.

Расшифровка ob_size

ob_size хранит количество элементов в ob_digit . Python переопределяет и затем использует значение ob_size для определения фактического количества элементов, содержащихся в массиве, чтобы повысить эффективность выделения памяти массиву ob_digit .

Хранение

Самый наивный способ хранить числа типа integer – это хранить одну десятичную цифру в одном элементе массива, тогда операции, такие как сложение и вычитание, могут выполняться по правилам математики из начальной школы.

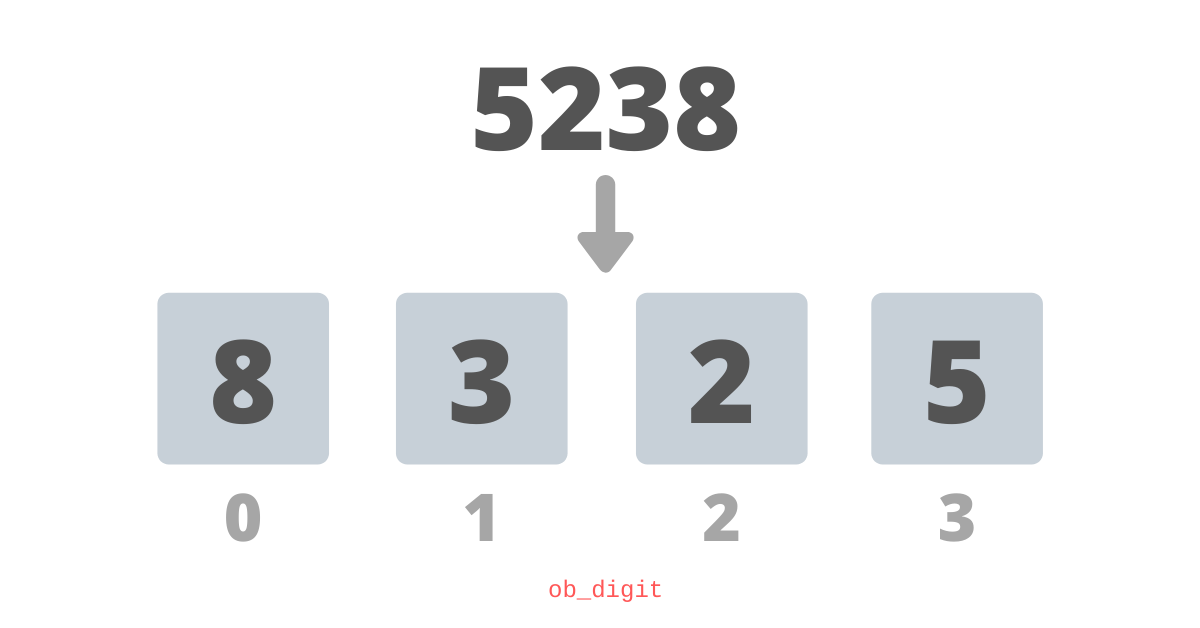
С таким подходом число 5238 будет сохранено так:

Такой подход неэффективен, поскольку мы будем использовать до 32-бит цифр (uint32_t) для хранения десятичной цифры, которая, по сути, колеблется от 0 до 9 и может быть легко представлена всего лишь 4 битами, ведь при написании чего-то столь же универсального как python, разработчик ядра должен быть еще изобретательнее.

Итак, можем ли мы сделать лучше? Конечно, иначе я бы не выложил эту статью. Давайте подробнее рассмотрим то, как Python хранит сверхдлинное целое число.

Путь Python

Вместо того, чтобы хранить только одну десятичную цифру в каждом элементе массива ob_digit , Python преобразует числа из системы счисления с основанием 10 в числа в системе с основанием 2 30 и вызывает каждый элемент, как цифру, значение которой колеблется от 0 до 2 30 — 1.

В шестнадцатеричной системе счисления, основание 16 ~ 2 4 означает, что каждая «цифра» шестнадцатеричного числа колеблется от 0 до 15 в десятичной системе счисления. В Python аналогично, «число» с основанием 2 30 , что означает, что число будет варьироваться от 0 до 2 30 – 1 = 1073741823 в десятичной системе счисления.

Таким образом, Python эффективно использует почти все выделенное пространство в 32 бита на одну цифру, экономит ресурсы и все еще выполняет простые операции, такие как сложение и вычитание на уровне математики начальной школы.

В зависимости от платформы Python использует либо 32-битные целочисленные беззнаковые массивы, либо 16-битные целочисленные беззнаковые массивы с 15-битными цифрами. Для выполнения операций, которые будут рассмотрены дальше, понадобится всего несколько битов.

Пример: 1152921504606846976

Как уже упоминалось, для Python числа представлены в системе с основанием 2 30 , то есть если вы конвертируете 1152921504606846976 в систему счисления с основанием 2 30 , вы получите 100.

1152921504606846976 = 1 * (2 30 ) 2 + 0 * (2 30 ) 1 + 0 * (2 30 ) 0

Поскольку ob_digit первым хранит наименее значащую цифру, оно сохраняется как 001 в виде трех цифр.

Структура _longobject для этого значения будет содержать:

• ob_size как 3
• ob_digit как [0, 0, 1]

Я создал демонстрационный REPL, который покажет, как внутри себя Python хранит integer, а также ссылается на члены структуры, такие как ob_size , ob_refcount и т. д.

Операции над длинными числами типа integer

Теперь, когда у нас есть четкое представление о том, как Python реализует целые числа произвольной точности, настало время понять, как с ними выполняются различные математические операции.

Сложение

Целые числа хранятся «в цифрах», это означает, что сложение выполняется также просто, как в начальной школе, и исходный код Python показывает нам, что именно так сложение и реализовано. Функция с именем x_add в файле longobject.c выполняет сложение двух чисел.

. for (i = 0; i < size_b; ++i) < carry += a->ob_digit[i] + b->ob_digit[i]; z->ob_digit[i] = carry & PyLong_MASK; carry >>= PyLong_SHIFT; > for (; i < size_a; ++i) < carry += a->ob_digit[i]; z->ob_digit[i] = carry & PyLong_MASK; carry >>= PyLong_SHIFT; > z->ob_digit[i] = carry; . 

Приведенный выше фрагмент кода взят из функции x_add . Как видите, она перебирает число по цифрам и выполняет сложение цифр, вычисляет результат и добавляет перенос.

Интереснее становится, когда результатом сложения является отрицательное число. Знак ob_size является знаком integer’а, то есть, если у вас есть отрицательное число, то ob_size будет минусом. Значение ob_size по модулю будет определять количество цифр в ob_digit .

Вычитание

Подобно тому, как происходит сложение, происходит и вычитание. Функция с именем x_sub в файле longobject.c выполняет вычитание одного числа из другого.

. for (i = 0; i < size_b; ++i) < borrow = a->ob_digit[i] - b->ob_digit[i] - borrow; z->ob_digit[i] = borrow & PyLong_MASK; borrow >>= PyLong_SHIFT; borrow &= 1; /* Keep only one sign bit */ > for (; i < size_a; ++i) < borrow = a->ob_digit[i] - borrow; z->ob_digit[i] = borrow & PyLong_MASK; borrow >>= PyLong_SHIFT; borrow &= 1; /* Keep only one sign bit */ > . 

Приведенный выше фрагмент кода взят из функции x_sub . В нем вы видите, как происходит перебор цифр и выполняется вычитание, вычисляется результат и распространяется перенос. Действительно, очень похоже на сложение.

Умножение

И снова умножение будет реализовано тем же наивным способом, который мы узнали из уроков математики в начальной школе, но он не отличается эффективностью. Чтобы поддерживать эффективность, Python реализует алгоритм Карацубы, который умножает два n-значных числа за O( n log ₂ 3 ) простых шагов.

Алгоритм непростой и его реализация выходит за рамки данной статьи, но вы можете найти его реализацию в функциях k_mul и k_lopsided_mul в файле longobject.c .

Деление и другие операции

Все операции над целыми числами определены в файле longobject.c , их очень просто найти и проследить работу каждой. Внимание: Детальное понимание работы каждой из них займет время, поэтому заранее запаситесь попкорном.

Оптимизация часто используемых целых чисел

Python заранее выделяет в памяти небольшое количество целых чисел в диапазоне от -5 до 256. Это выделение происходит во время инициализации, и поскольку мы не можем изменить целые числа (иммутабельность), эти предварительно выделенные числа являются синглтонами и на них ссылаются напрямую вместо реаллокации. Это значит, что каждый раз, когда мы используем/создаем маленькое число, Python вместо реаллокации просто возвращает ссылку на предварительно аллоцированное число.

Такую оптимизацию можно проследить в макросе IS_SMALL_INT и функции get_small_int в longobject.c . Так Python экономит много места и времени на вычисление часто используемых чисел типа integer.

Это вторая статья из серии Python Internals. Первая статья была о том, как я изменил свою версию Python, сделав его двусмысленным. Она поможет вам сделать первые шаги в понимании исходного кода Python и продолжить путь к становлению разработчиком ядра Python.

Если вы хотите увидеть больше похожих статей, подпишитесь на мою рассылку и получайте их прямо в свой почтовый ящик. Я пишу об инженерии, системном проектировании и немного о программировании каждую пятницу. Пишите мне на @arpit_bhayani. Мои предыдущие статьи вы найдете на @arpitbhayani.me/blogs.

На этом все. До встречи на курсе!

Источник

Деление больших чисел в Python

Я предполагаю, что я не говорю Python, как правильно обрабатывать большие числа, но я не знаю, куда идти дальше.

Я также должен добавить, что конечной целью является расчет

максимально длинный и точный

6 ответов

Расширяю свой комментарий, если N а также f2 являются long строго больше 0, то

это точно ceil(N / float(f2)) (но даже более точно, чем использование поплавков).

(Использование // скорее, чем / для целочисленного деления — для совместимости с Python 3.x без лишних усилий.)

Это потому что N // f2 дает вам (в основном) floor(N / float(f2)) так что N // f2 + 1 почти всегда так же, как ceil , Однако когда N это кратное f2 , N // f2 + 1 слишком большой ( +1 не должно быть там), но с помощью N — 1 исправляет это и не нарушает другой случай.

(Это не работает ни для N , f2 меньше или равно 0, но это может быть обработано отдельно)

fmin это float после того, как вы разделите длинное целое число на число с плавающей точкой. Его ценность 1.84952718165824e+305 , Добавление 1 к этому ничего не меняет, точность просто не так высока.

Если вы вместо этого сделаете целочисленное деление, fmin остается long :

>>> fmin = N / f2 >>> fmin 18495271816582402193321106509793602189617847415669131056768139225220221855498293 49983070478076000952025038039460539798061570960870927236986153971731443029057201 52035339202255934728764897424408896865977423536890485615063959262845076766281553 766072964756078264853041334880929452289298495368916583660903481130L >>> N - (fmin * f2) 111L 

Конечно, вы не получаете 0 из-за целочисленного деления, где отбрасывается десятичная часть результата. Но теперь добавление 1 будет иметь значение:

С использованием Decimal модуль не меняет проблему:

>>> from decimal import Decimal, getcontext >>> fmin = Decimal(N) / Decimal(f2) >>> fmin Decimal('1.849527181658240219332110651E+305') 

Там все еще нет безграничной точности, и даже если вы установите Decimal.getcontext().prec = 2000 , вы все равно не получите точно 0.

Источник