Cubic spline interpolation in python

scipy.interpolate.CubicSpline#

Interpolate data with a piecewise cubic polynomial which is twice continuously differentiable [1]. The result is represented as a PPoly instance with breakpoints matching the given data.

Parameters : x array_like, shape (n,)

1-D array containing values of the independent variable. Values must be real, finite and in strictly increasing order.

y array_like

Array containing values of the dependent variable. It can have arbitrary number of dimensions, but the length along axis (see below) must match the length of x . Values must be finite.

axis int, optional

Axis along which y is assumed to be varying. Meaning that for x[i] the corresponding values are np.take(y, i, axis=axis) . Default is 0.

bc_type string or 2-tuple, optional

Boundary condition type. Two additional equations, given by the boundary conditions, are required to determine all coefficients of polynomials on each segment [2].

If bc_type is a string, then the specified condition will be applied at both ends of a spline. Available conditions are:

• ‘not-a-knot’ (default): The first and second segment at a curve end are the same polynomial. It is a good default when there is no information on boundary conditions.
• ‘periodic’: The interpolated functions is assumed to be periodic of period x[-1] — x[0] . The first and last value of y must be identical: y[0] == y[-1] . This boundary condition will result in y'[0] == y'[-1] and y»[0] == y»[-1] .
• ‘clamped’: The first derivative at curves ends are zero. Assuming a 1D y, bc_type=((1, 0.0), (1, 0.0)) is the same condition.
• ‘natural’: The second derivative at curve ends are zero. Assuming a 1D y, bc_type=((2, 0.0), (2, 0.0)) is the same condition.

If bc_type is a 2-tuple, the first and the second value will be applied at the curve start and end respectively. The tuple values can be one of the previously mentioned strings (except ‘periodic’) or a tuple (order, deriv_values) allowing to specify arbitrary derivatives at curve ends:

• order: the derivative order, 1 or 2.
• deriv_value: array_like containing derivative values, shape must be the same as y, excluding axis dimension. For example, if y is 1-D, then deriv_value must be a scalar. If y is 3-D with the shape (n0, n1, n2) and axis=2, then deriv_value must be 2-D and have the shape (n0, n1).

If bool, determines whether to extrapolate to out-of-bounds points based on first and last intervals, or to return NaNs. If ‘periodic’, periodic extrapolation is used. If None (default), extrapolate is set to ‘periodic’ for bc_type=’periodic’ and to True otherwise.

PCHIP 1-D monotonic cubic interpolator.

Piecewise polynomial in terms of coefficients and breakpoints.

Parameters bc_type and extrapolate work independently, i.e. the former controls only construction of a spline, and the latter only evaluation.

When a boundary condition is ‘not-a-knot’ and n = 2, it is replaced by a condition that the first derivative is equal to the linear interpolant slope. When both boundary conditions are ‘not-a-knot’ and n = 3, the solution is sought as a parabola passing through given points.

When ‘not-a-knot’ boundary conditions is applied to both ends, the resulting spline will be the same as returned by splrep (with s=0 ) and InterpolatedUnivariateSpline , but these two methods use a representation in B-spline basis.

Carl de Boor, “A Practical Guide to Splines”, Springer-Verlag, 1978.

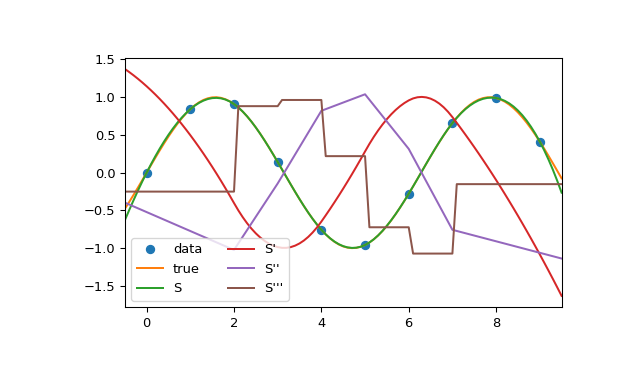
In this example the cubic spline is used to interpolate a sampled sinusoid. You can see that the spline continuity property holds for the first and second derivatives and violates only for the third derivative.

>>> import numpy as np >>> from scipy.interpolate import CubicSpline >>> import matplotlib.pyplot as plt >>> x = np.arange(10) >>> y = np.sin(x) >>> cs = CubicSpline(x, y) >>> xs = np.arange(-0.5, 9.6, 0.1) >>> fig, ax = plt.subplots(figsize=(6.5, 4)) >>> ax.plot(x, y, 'o', label='data') >>> ax.plot(xs, np.sin(xs), label='true') >>> ax.plot(xs, cs(xs), label="S") >>> ax.plot(xs, cs(xs, 1), label="S'") >>> ax.plot(xs, cs(xs, 2), label="S''") >>> ax.plot(xs, cs(xs, 3), label="S'''") >>> ax.set_xlim(-0.5, 9.5) >>> ax.legend(loc='lower left', ncol=2) >>> plt.show() 

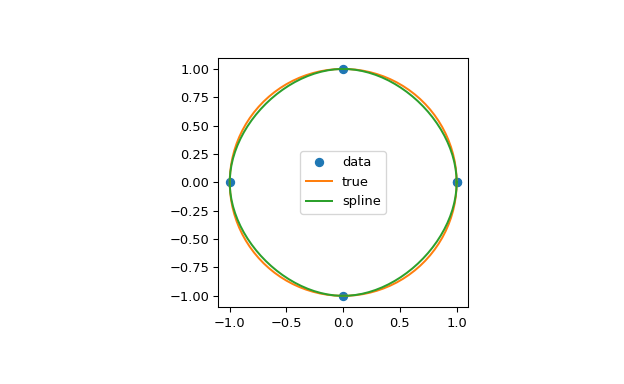
In the second example, the unit circle is interpolated with a spline. A periodic boundary condition is used. You can see that the first derivative values, ds/dx=0, ds/dy=1 at the periodic point (1, 0) are correctly computed. Note that a circle cannot be exactly represented by a cubic spline. To increase precision, more breakpoints would be required.

>>> theta = 2 * np.pi * np.linspace(0, 1, 5) >>> y = np.c_[np.cos(theta), np.sin(theta)] >>> cs = CubicSpline(theta, y, bc_type='periodic') >>> print("ds/dx=  ds/dy= ".format(cs(0, 1)[0], cs(0, 1)[1])) ds/dx=0.0 ds/dy=1.0 >>> xs = 2 * np.pi * np.linspace(0, 1, 100) >>> fig, ax = plt.subplots(figsize=(6.5, 4)) >>> ax.plot(y[:, 0], y[:, 1], 'o', label='data') >>> ax.plot(np.cos(xs), np.sin(xs), label='true') >>> ax.plot(cs(xs)[:, 0], cs(xs)[:, 1], label='spline') >>> ax.axes.set_aspect('equal') >>> ax.legend(loc='center') >>> plt.show() 

>>> cs = CubicSpline([0, 1], [0, 1], bc_type=((1, 0), (1, 3))) >>> x = np.linspace(0, 1) >>> np.allclose(x**3, cs(x)) True 

Breakpoints. The same x which was passed to the constructor.

c ndarray, shape (4, n-1, …)

Coefficients of the polynomials on each segment. The trailing dimensions match the dimensions of y, excluding axis . For example, if y is 1-d, then c[k, i] is a coefficient for (x-x[i])**(3-k) on the segment between x[i] and x[i+1] .

Interpolation axis. The same axis which was passed to the constructor.

Evaluate the piecewise polynomial or its derivative.

Construct a new piecewise polynomial representing the derivative.

Construct a new piecewise polynomial representing the antiderivative.

Compute a definite integral over a piecewise polynomial.

Find real roots of the piecewise polynomial.

Источник

How to perform cubic spline interpolation in python?

Interpolation is a technique used to estimate the value of a function at a point where the function is not defined. One commonly used method for interpolation is cubic spline interpolation, which involves constructing a piecewise cubic polynomial that passes through a set of data points. In this tutorial, we will discuss how to perform cubic spline interpolation in Python.

Method 1: Using the scipy.interpolate library

Cubic spline interpolation is a mathematical method that is used to construct new data points within the range of a discrete set of known data points. In Python, we can perform cubic spline interpolation using the scipy.interpolate library.

Step 1: Import the necessary libraries

import numpy as np from scipy.interpolate import CubicSpline import matplotlib.pyplot as plt

Step 2: Define the known data points

x = np.array([0, 1, 2, 3, 4, 5]) y = np.array([0, 2, 1, 4, 3, 5])

Step 3: Create a cubic spline object

Step 4: Evaluate the cubic spline at desired points

xs = np.arange(0, 5.1, 0.1) ys = cs(xs)

Step 5: Plot the results

plt.plot(x, y, 'o', label='data') plt.plot(xs, ys, label='cubic spline') plt.legend() plt.show()

The above code will create a cubic spline object, evaluate it at desired points, and plot the results. You can adjust the range of xs and the step size to change the number of points to evaluate the cubic spline at.

This is just one example of how to perform cubic spline interpolation in Python using the scipy.interpolate library. There are many other methods and options available in this library, so be sure to check the documentation for more information.

Method 2: Using the numpy.polyfit and numpy.poly1d functions

Cubic spline interpolation is a mathematical technique used to interpolate a set of data points using a cubic polynomial. In Python, we can use the numpy.polyfit and numpy.poly1d functions to perform cubic spline interpolation.

Step 1: Importing the Required Libraries

We will be using the numpy library for performing the cubic spline interpolation. So, we need to import the numpy library.

Step 2: Defining the Data Points

We need to define the data points that we want to interpolate. Let’s assume that we have the following data points:

x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 1, 3, 5, 4])

Step 3: Performing the Cubic Spline Interpolation

We can perform the cubic spline interpolation using the numpy.polyfit and numpy.poly1d functions as follows:

coefficients = np.polyfit(x, y, 3) polynomial = np.poly1d(coefficients) x_interpolated = np.linspace(x[0], x[-1], 100) y_interpolated = polynomial(x_interpolated)

In the above code, we first calculate the coefficients of the cubic polynomial that interpolates the data points using the numpy.polyfit function. We then create a polynomial function from the coefficients using the numpy.poly1d function. We define the range of values for which we want to interpolate the data points using the numpy.linspace function. Finally, we evaluate the polynomial function at the interpolated values using the polynomial function.

Step 4: Plotting the Interpolated Data Points

We can plot the interpolated data points using the matplotlib library as follows:

import matplotlib.pyplot as plt plt.scatter(x, y) plt.plot(x_interpolated, y_interpolated) plt.show()

In the above code, we first import the matplotlib library. We then plot the original data points using the matplotlib.pyplot.scatter function. We plot the interpolated data points using the matplotlib.pyplot.plot function. Finally, we show the plot using the matplotlib.pyplot.show function.

Full Code Example

import numpy as np import matplotlib.pyplot as plt x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 1, 3, 5, 4]) coefficients = np.polyfit(x, y, 3) polynomial = np.poly1d(coefficients) x_interpolated = np.linspace(x[0], x[-1], 100) y_interpolated = polynomial(x_interpolated) plt.scatter(x, y) plt.plot(x_interpolated, y_interpolated) plt.show()

This is how we can perform cubic spline interpolation in Python using the numpy.polyfit and numpy.poly1d functions.

Method 3: Using the scikit-learn library

To perform cubic spline interpolation in Python using the scikit-learn library, you can use the SplineTransformer class. Here are the steps to do it:

from sklearn.preprocessing import SplineTransformer import numpy as np

x = np.array([1, 2, 3, 4, 5]) y = np.array([2, 4, 1, 3, 5])

spline_transformer = SplineTransformer(degree=degree)

X_spline = spline_transformer.fit_transform(x.reshape(-1, 1))

new_x = np.array([1.5, 2.5, 3.5]) new_y = spline_transformer.transform(new_x.reshape(-1, 1))

This will output the transformed data and the predicted values for the new input:

[[ 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] [[2.16666667] [3. ] [3.33333333]]

This is how you can perform cubic spline interpolation in Python using the scikit-learn library.

Источник