Расширенная анимация CSS с использованием cubic-bezier()
От автора: имея дело со сложной анимацией CSS, есть тенденция создавать экспансивные @keyframes с большим количеством объявлений. Однако есть пара приемов, о которых я хочу поговорить, они могут помочь упростить задачу, оставаясь при этом ванильным CSS.
Первый более широко используется и знаком многим, а второй менее распространен. Для этого могут быть веские причины — объединять анимации с помощью запятых относительно проще, чем разбираться в различных доступных нам функциях синхронизации и том, что они делают. Есть одна особенно удобная функция синхронизации, которая дает нам полный контроль над созданием пользовательской функций времени. Это cubic-bezier() и в этом посте я покажу вам ее силу и то, как ее можно использовать для создания чудесной анимации без особой сложности.
Начнем с базового примера, показывающего, как мы можем перемещать мяч в определённых направлениях, например, в форме бесконечности (∞):
Онлайн курс по JavaScript
Научитесь создавать приложения со сложными интерфейсами
Это основной язык для современной веб-разработки — почти 100% сайтов работает на JavaScript. Освойте его с нуля всего за 4 месяца, и вы сможете зарабатывать от 70 000 рублей.
Как видите, здесь нет сложного кода — только два ключевых кадра и функция cubic-bezier(). И все же мы получаем довольно сложную финальную анимацию бесконечной формы. Круто, правда? Давайте вникнем в это!
Функция cubic-bezier()
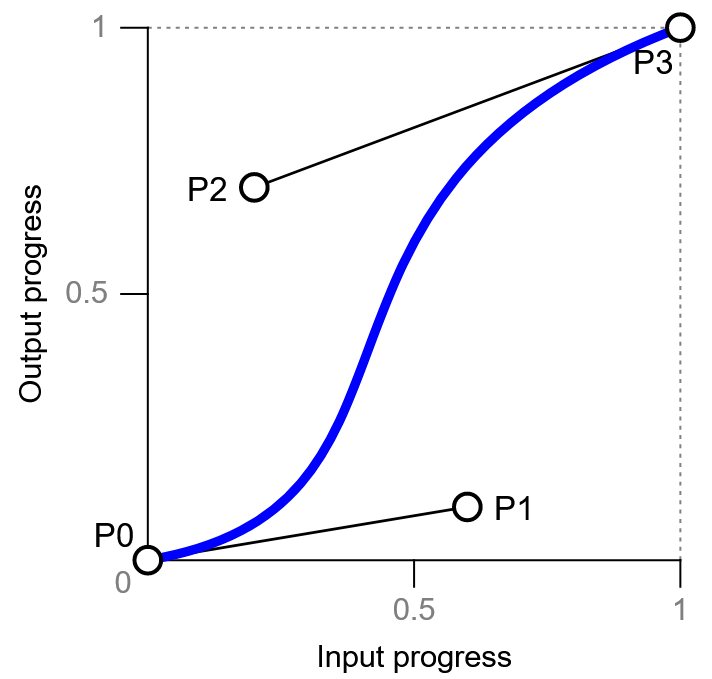
Начнем с официального определения: Кубическая функция ослабления Безье — это тип функции ослабления, определяемый четырьмя действительными числами, которые определяют две контрольные точки, P1 и P2, кубической кривой Безье, конечные точки P0 и P3 которой фиксированы в (0, 0) и (1, 1) соответственно. Координаты x P1 и P2 ограничены диапазоном [0, 1].
Вышеупомянутая кривая определяет, как выходные данные (ось y) будут вести себя в зависимости от времени (ось x). Каждая ось имеет диапазон [0, 1](или [0% 100%]). Если у нас есть анимация, которая длится две секунды (2s), то:
Если мы хотим анимировать left от 5px до 20px, то:
X, время, всегда ограничено [0 1]; однако Y может выходить за рамки [0 1]. Моя цель — отрегулировать P1 и P2, чтобы создать следующие кривые:
Вы можете подумать, что этого невозможно достичь, потому что, как указано в определении, P0 и P3 фиксированы (0,0) и (1,1) и это означает, что они не могут находиться на одной оси. Это правда, и мы воспользуемся некоторыми математическими приемами, чтобы «приблизительно» их «аппроксимировать».
Параболическая кривая
Давайте начнем со следующим определением: cubic-bezier(0,1.5,1,1.5). Это дает нам следующую кривую:
Наша цель — двигаться от (1,1) до (0,1) и делать то, что технически невозможно. Так что попробуем построить фейковою кривую.
Ранее мы говорили, что наш диапазон равен [0 1] (или [0% 100%]), поэтому давайте представим случай, когда 0% он очень близок к 100%. Если, например, мы хотим анимировать top от 20px (0%) до, 20.1px (100%) то мы можем сказать, что начальное и конечное состояния равны.
Хм, наш элемент вообще не двинется? Ну, он немного сдвинется, потому что значение Y превышает 20.1px( 100%). Но этого недостаточно, чтобы дать нам ощутимое движение:
Давайте обновим кривую и будем использовать cubic-bezier(0,4,1,4) вместо нее. Обратите внимание на то, что наша кривая стала намного выше, чем раньше:
Но все равно движения нет — даже если верхнее значение пересекает 3 (или 300%). Попробуем cubic-bezier(0,20,1,20):
Да! Он начал немного двигаться. Вы заметили изменение кривой каждый раз, когда мы увеличиваем значение? Это делает нашу точку (1,1) «визуально» ближе к тому моменту (0,1) когда мы уменьшаем масштаб, чтобы увидеть полную кривую, и это уловка.
Используя cubic-bezier(0,V,1,V) где V- какое-то очень большое значение, а начальное и конечное состояния очень близки (или почти равны), мы можем моделировать параболическую кривую. Пример стоит тысячи слов:
Я применил «волшебную» кубическую функцию Безье к анимации top, а также применил к ней линейную left. Это дает нам желаемую кривую.
Копаемся в математике
Для тех из вас, кто разбирается в математике, мы можем разбить это объяснение дальше. Кубический Безье можно определить по следующей формуле: