Clustering visualization example python

Реализация кластеризации методом k-средних на Python (с визуализацией)

Кластеризация — разбиение множества объектов на подмножества, называемые кластерами. Кластеризация, будучи математическим алгоритм имеет широкое применение во многих сферах: начиная с таких естественно научных областей как биология и физиология, и заканчивая маркетингом в социальных сетях и поисковой оптимизацией.

Существует множество алгоритмов кластеризации, однако ниже будет рассмотрен метод k-средних, так как он является наиболее лаконичным и простым для понимания.

Кластеризация методом k-средних:

Исходной задачей будет распределение произвольного количества n-мерных точек по k кластерам.

1. Случайным образом создаются k точек, в дальнейшем будем называть их центрами кластеров;
2. Для каждой точки ставится в соответствии ближайший к ней центр кластера;
3. Вычисляются средние арифметические точек, принадлежащих к определённому кластеру. Именно эти значения становятся новыми центрами кластеров;
4. Шаги 2 и 3 повторяются до тех пор, пока пересчёт центров кластеров будет приносить плоды. Как только высчитанные центры кластеров совпадут с предыдущими, алгоритм будет окончен.

Приступим к реализации алгоритма:

Исходные данные алгоритма:

• n — количество строк;
• k — количество кластеров;
• dim — размерность точек (пространства).

Выходные данные алгоритма:

• cluster — двумерный массив размерностью dim * k, содержащий k точек — центры кластеров;
• cluster_content — массив, содержащий в себе k массивов — массивов точек принадлежащих соответствующему кластеру.

def clusterization(array, k): n = len(array) dim = len(array[0]) cluster = [[0 for i in range(dim)] for q in range(k)] cluster_content = [[] for i in range(k)] for i in range(dim): for q in range(k): cluster[q][i] = random.randint(0, max_cluster_value) cluster_content = data_distribution(array, cluster)

Переменные заданы. Первичные центры кластеров созданы с помощью библиотеки random(стр. 9 — 11) max_claster_value — константа задающая примерные границы исходного множества;

При помощи функции data_ditribution() произведено первичное распределения точек по кластерам (стр. 13). Рассмотрим эту функцию подробнее:

def data_distribution(array, cluster): cluster_content = [[] for i in range(k)] for i in range(n): min_distance = float('inf') situable_cluster = -1 for j in range(k): distance = 0 for q in range(dim): distance += (array[i][q]-cluster[j][q])**2 distance = distance**(1/2) if distance < min_distance: min_distance = distance situable_cluster = j cluster_content[situable_cluster].append(array[i]) return cluster_content

Для каждой строчки (стр. 5) высчитывается расстояние до каждого центра кластеров. Здесь применяется стандартный алгоритм:

1. За начальное кратчайшее расстояние (min_distance) берётся несоизмеримо большое со значениями точек число;
2. Затем происходит вычисление расстояния до центра каждого кластера;
3. Если вычисленное расстояние меньше минимального, то минимальное расстояние приравнивается к вычисленному и точка привязывается к этому кластеру (situable_cluster);
4. После обработки точки, в массив cluster_content в выбранный кластер (situable_cluster) кластер вкладывается значение точки.

Функция возвращает массив cluster_content.

В дальнейшем, как и полагается, данная последовательность действий обращается в цикл:

privious_cluster = copy.deepcopy(cluster) while 1: cluster = cluster_update(cluster, cluster_content, dim) cluster_content = data_distribution(array, cluster) if cluster == privious_cluster: break privious_cluster = copy.deepcopy(cluster)

Данный цикл целостным образом описывает шаг 4 из описании алгоритм k-средних (см. выше).

После распределения точек по центрам кластеров происходит перераспределение уже центров кластеров по привязанным к ним точкам (стр. 2). Рассмотрим функцию cluster_content() подробнее:

def cluster_update(cluster, cluster_content, dim): k = len(cluster) for i in range(k): #по i кластерам for q in range(dim): #по q параметрам updated_parameter = 0 for j in range(len(cluster_content[i])): updated_parameter += cluster_content[i][j][q] if len(cluster_content[i]) != 0: updated_parameter = updated_parameter / len(cluster_content[i]) cluster[i][q] = updated_parameter return cluster

Для каждого кластера, для каждого из n измерений вычисляется новое значения с помощью незамысловатого среднего арифметического: стр. 8-9 — складываются все значения; стр. 11-12 — сумма делится на количество точек в кластере; стр. 13 — кластер принимает обновлённое значение.

На данном месте алгоритм заканчивает свою работу. Полный алгоритм выглядит следующим образом:

def clusterization(array, k): n = len(array) dim = len(array[0]) cluster = [[0 for i in range(dim)] for q in range(k)] cluster_content = [[] for i in range(k)] for i in range(dim): for q in range(k): cluster[q][i] = random.randint(0, max_cluster_value) cluster_content = data_distribution(array, cluster) privious_cluster = copy.deepcopy(cluster) while 1: cluster = cluster_update(cluster, cluster_content, dim) cluster_content = data_distribution(array, cluster) if cluster == privious_cluster: break privious_cluster = copy.deepcopy(cluster)

Перейдём к визуализации:

Визуализируем результат алгоритма для 3-х и 2-х мерного исходных пространств. Воспользуемся библиотекой mathplotlib:

import matplotlib.pyplot as plt from mpl_toolkits import mplot3d import numpy as np

Визуализация для 2-х мерного пространства происходит следующим образом:

def visualisation_2d(cluster_content): k = len(cluster_content) plt.grid() plt.xlabel("x") plt.ylabel("y") for i in range(k): x_coordinates = [] y_coordinates = [] for q in range(len(cluster_content[i])): x_coordinates.append(cluster_content[i][q][0]) y_coordinates.append(cluster_content[i][q][1]) plt.scatter(x_coordinates, y_coordinates) plt.show()

Grid() — создание сетки. xlabel(), ylabel() — названия осей. Затем в массивы, соответствующие осям вкладываются значения точек. После такой операции для каждого кластера вызывается функция scatter() — разброс точек по плоскости. В конце вызывается функция отображения — show().

Аналогичным образом визуализируется результат алгоритма для 3-х мерного пространства:

def visualisation_3d(cluster_content): ax = plt.axes(projection="3d") plt.xlabel("x") plt.ylabel("y") k = len(cluster_content) for i in range(k): x_coordinates = [] y_coordinates = [] z_coordinates = [] for q in range(len(cluster_content[i])): x_coordinates.append(cluster_content[i][q][0]) y_coordinates.append(cluster_content[i][q][1]) z_coordinates.append(cluster_content[i][q][2]) ax.scatter(x_coordinates, y_coordinates, z_coordinates) plt.show()

Таким образом, мы выполнили необходимые и достаточные условия для анализа и реализации кластеризации методом k-средних.

Источник

How to Plot K-Means Clusters with Python?

In this article we’ll see how we can plot K-means Clusters.

K-means Clustering is an iterative clustering method that segments data into k clusters in which each observation belongs to the cluster with the nearest mean (cluster centroid).

Steps for Plotting K-Means Clusters

This article demonstrates how to visualize the clusters. We’ll use the digits dataset for our cause.

1. Preparing Data for Plotting

First Let’s get our data ready.

#Importing required modules from sklearn.datasets import load_digits from sklearn.decomposition import PCA from sklearn.cluster import KMeans import numpy as np #Load Data data = load_digits().data pca = PCA(2) #Transform the data df = pca.fit_transform(data) df.shape

Digits dataset contains images of size 8×8 pixels, which is flattened to create a feature vector of length 64. We used PCA to reduce the number of dimensions so that we can visualize the results using a 2D Scatter plot.

2. Apply K-Means to the Data

Now, let’s apply K-mean to our data to create clusters.

Here in the digits dataset we already know that the labels range from 0 to 9, so we have 10 classes (or clusters).

But in real-life challenges when performing K-means the most challenging task is to determine the number of clusters.

There are various methods to determine the optimum number of clusters, i.e. Elbow method, Average Silhouette method. But determining the number of clusters will be the subject of another talk.

#Import required module from sklearn.cluster import KMeans #Initialize the class object kmeans = KMeans(n_clusters= 10) #predict the labels of clusters. label = kmeans.fit_predict(df) print(label)

kmeans.fit_predict method returns the array of cluster labels each data point belongs to.

3. Plotting Label 0 K-Means Clusters

Now, it’s time to understand and see how can we plot individual clusters.

The array of labels preserves the index or sequence of the data points, so we can utilize this characteristic to filter data points using Boolean indexing with numpy.

Let’s visualize cluster with label 0 using the matplotlib library.

import matplotlib.pyplot as plt #filter rows of original data filtered_label0 = df[label == 0] #plotting the results plt.scatter(filtered_label0[:,0] , filtered_label0[:,1]) plt.show()

The code above first filters and keeps the data points that belong to cluster label 0 and then creates a scatter plot.

See how we passed a Boolean series to filter [label == 0]. Indexed the filtered data and passed to plt.scatter as (x,y) to plot. x = filtered_label0[:, 0] , y = filtered_label0[:, 1].

4. Plotting Additional K-Means Clusters

Now, that we have some idea, let’s plot clusters with label 2 and 8.

#filter rows of original data filtered_label2 = df[label == 2] filtered_label8 = df[label == 8] #Plotting the results plt.scatter(filtered_label2[:,0] , filtered_label2[:,1] , color = 'red') plt.scatter(filtered_label8[:,0] , filtered_label8[:,1] , color = 'black') plt.show()

5. Plot All K-Means Clusters

Now, that we got the working mechanism let’s apply it to all the clusters.

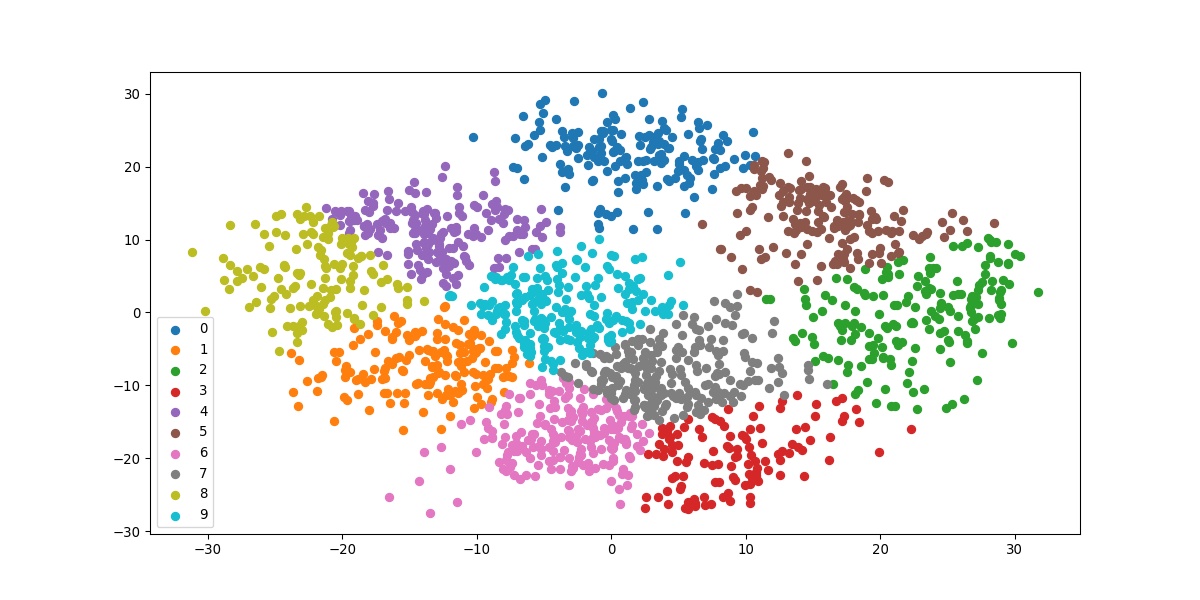
#Getting unique labels u_labels = np.unique(label) #plotting the results: for i in u_labels: plt.scatter(df[label == i , 0] , df[label == i , 1] , label = i) plt.legend() plt.show()

The above code iterates filtering the data according to each unique class one iteration at a time. The result we get is the final visualization of all the clusters.

6. Plotting the Cluster Centroids

#Getting the Centroids centroids = kmeans.cluster_centers_ u_labels = np.unique(label) #plotting the results: for i in u_labels: plt.scatter(df[label == i , 0] , df[label == i , 1] , label = i) plt.scatter(centroids[:,0] , centroids[:,1] , s = 80, color = 'k) plt.legend() plt.show()

kmeans.cluster_centers_ return an array of centroids locations.

Here’s the complete code of what we just saw above.

#Importing required modules from sklearn.datasets import load_digits from sklearn.decomposition import PCA from sklearn.cluster import KMeans import numpy as np #Load Data data = load_digits().data pca = PCA(2) #Transform the data df = pca.fit_transform(data) #Import KMeans module from sklearn.cluster import KMeans #Initialize the class object kmeans = KMeans(n_clusters= 10) #predict the labels of clusters. label = kmeans.fit_predict(df) #Getting unique labels u_labels = np.unique(label) #plotting the results: for i in u_labels: plt.scatter(df[label == i , 0] , df[label == i , 1] , label = i) plt.legend() plt.show()

Conclusion

In this article, we saw how we can visualize the clusters formed by the k-means algorithm. Till we meet next time, Happy Learning!

Источник