Число компонент связности
Задача:
Дан неориентированный невзвешенный граф. Необходимо посчитать количество его компонент связности и вывести их. Во входном файле записано два числа N и M (0 < N ≤ 100000, 0 ≤ M ≤ 100000). В следующих M строках записаны по два числа i и j (1 ≤ i, j ≤ N), которые означают, что вершины i и j соединены ребром.
В первой строчке выходного файла выведите количество компонент связности. Далее выведите сами компоненты связности в следующем формате: в первой строке количество вершин в компоненте, во второй — сами вершины в порядке возрастания.
Пример:
Входные данные:
6 4
3 1
1 2
5 4
2 3
Выходные данные:
3
3
1 2 3
2
4 5
1
6
Код написал, но на определенном этапе превышает ограничение по времени (на 0.069 сек)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43
inp =list(map(int,input().split())) n,m = inp[0],inp[1] def ToDict(n,m): ribs = list() while m > 0: ribs.append(list(map(int, input().split()))) m -= 1 ribsDict = dict() for i in range(n): currRibs = [] for j in range(len(ribs)): if ribs[j][0] == i + 1: currRibs.append(ribs[j][1]) elif ribs[j][1] == i + 1: currRibs.append(ribs[j][0]) ribsDict[i + 1] = currRibs return ribsDict ribsDict = ToDict(n,m) Visited = [False]*(n + 1) def DFS(start,verts): Visited[start] = True verts.append(start) for u in ribsDict[start]: if not Visited[u]: DFS(u,verts) return verts comps = list() for i in range(1,n+1): if not Visited[i]: comps.append(DFS(i,list())) print(len(comps)) for i in range(len(comps)): print(len(comps[i])) print(' '.join(list(map(str,sorted(comps[i])))))
Анализ связности направленного графа с библиотекой Networkx в Google Colab
В рамках продвижения нашего нового курса по графовой аналитике больших данных в бизнес-приложениях, сегодня рассмотрим, что такое связность в графе, зачем вычислять компоненты связности и как это сделать для ориентированных графов. Продемонстрируем все вычисления с помощью методов Python-библиотеки Networkx в Google Colab.
Основы теории графов и применения Networkx в Google Colab на практическом примере
Напомним, граф называется связным, если для любой пары его различных вершин существует цепь, соединяющая эти вершины. Практический смысл связности графа отлично иллюстрирует сеть автомобильных дорог или линий метрополитена, спроектированные и реализованные так, что из любой точки отправления можно попасть в нужный пункт назначения. Поэтому дороги рекомендуется строить так, чтобы, чтобы связность получающегося графа неуклонно росла. Аналогичный вывод справедлив и для сайта, основную ценность которого составляет контент, например, соцсеть, интернет-журнал, тематический блог и пр.
Рассмотрим этот пример более подробно. Предположим, есть данные за сутки по переходам пользователей сайта: со страниц корпоративного блога на страницы продаваемых продуктов – образовательных курсов, а также между страницами блога. Входной точкой чаще всего является страница блога, куда пользователь пришел по ключевым словам в поисковом запросе, а затем перешел на страницу курса. Фрагмент датасета представлен на рисунке, где столбец node1 – это исходная страница блога, node2 – последующая страница курса или блога, а edge — количество переходов.
Графовые алгоритмы. Бизнес-приложения
Код курса
GRAF
Ближайшая дата курса
Длительность обучения
24 ак.часов
Стоимость обучения
66 000 руб.
Построим направленный (ориентированный) взвешенный граф по этим переходам с помощью Python-библиотеки Networkx в Google Colab. Эта библиотека написана на Python и свободно распространяется под лицензией BSD. Она предназначена для создания, манипуляции и анализа структуры, динамики и функционирования графовых структур. Хотя NetworkX имеет базовые функции визуализации графов, основная цель этого инструмента – анализ графов, а не визуализация. Поэтому для наглядного отображения графов рекомендуется использовать специализированные библиотеки, например, Matplotlib. Для этого ее следует также, как и NetworkX, импортировать в свой Python-скрипт. Если исходные данные для построения графа содержатся в списке, его следует преобразовать в датафрейм pandas, чтобы создать взвешенный граф из этого датафрейма. Таким образом, также необходим импорт библиотеки Pandas. Код на Python в Google Colab будет выглядеть так:
import networkx as nx import matplotlib.pyplot as plt import pandas as pd data = [('Blog_Page_1','COURSE_1',90),('Blog_Page_1','COURSE_2',212),('Blog_Page_1','Blog_Page_2',99),('Blog_Page_6','COURSE_1',58), ('Blog_Page_3','COURSE_4',401),('Blog_Page_3','COURSE_2',2),('Blog_Page_6','Blog_Page_2',309),('Blog_Page_1','COURSE_3',306), ('Blog_Page_3','Blog_Page_2',41),('Blog_Page_11','COURSE_1',122),('Blog_Page_2','Blog_Page_6',39),('Blog_Page_2','COURSE_4',224), ('Blog_Page_11','COURSE_3',201),('Blog_Page_11','COURSE_4',89),('Blog_Page_6','Blog_Page_3',309),('Blog_Page_1','Blog_Page_3',76) ] df = pd.DataFrame(data=data,columns=['node1','node2','edge']) graph=nx.DiGraph() graph.add_weighted_edges_from(data) pos = nx.spring_layout(graph, k=1000) nx.draw(graph, pos, with_labels=True) plt.show() Как проанализировать этот граф и вычислить его связность, рассмотрим далее.
Анализ связности графа
Связным называется граф, который содержит ровно одну компоненту связности, т.е. между любой парой его вершин существует как минимум один путь. В контексте одного узла вычисляют степень связности – число связей, инцидентных узлу, т.е. количество его ребер. В направленном графе определяются две меры степени связности: полустепень захода (число связей, входящих в узел) и полустепень исхода (число связей, исходящих из узла). Например, если рассматривать связь как дружбу или сотрудничество, полустепень захода показывает популярность человека, а полустепень исхода – его общительность. Это полезно при анализе социальных связей, о чем мы писали здесь.
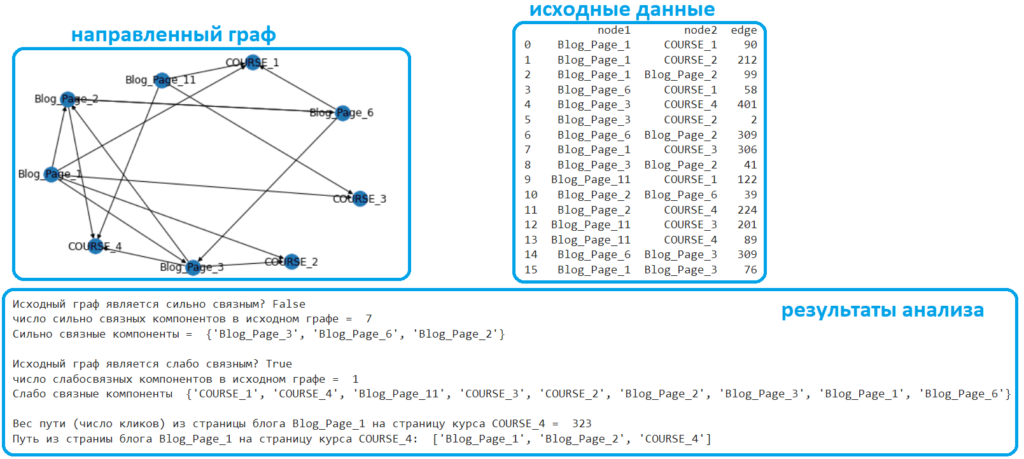
Возвращаясь к анализу всего графа переходов по страницам сайта, определим, является ли он сильно связным или слабо связным. Ориентированный граф считается слабо связным, если соответствующий ему неориентированный граф является связным. Иначе говоря, для ориентированного графа компонент слабой связности — это подграф исходного графа, где все вершины соединены друг с другом некоторым путем, игнорируя направление ребер.
Направленный граф считается сильно связным, если его каждая вершина достижима из любой другой вершины. Компонентой сильной связности ориентированного графа называется максимальный по включению сильно связный подграф. Другими словами, это подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин. Компонента сильной связности — это часть ориентированного графа, в которой существует путь из каждой вершины в другую вершину.
Ответить на вопрос, является ли рассматриваемый граф сильно связным или слабо связным, помогут соответствующие методы библиотеки NetworkX: is_strongly_connected(G) и is_weakly_connected(G), которые возвращают значения True или False. В качестве параметра G следует указать имя графа. Также рассчитаем количество сильно и слабо связных компонентов в графе с помощью методов nx.number_strongly_connected_components(G) и nx.number_ weakly _connected_components(G). Еще выведем самый большой сильный и самый большой слабый связные компоненты исходного графа.
print('\nИсходный граф является сильно связным?', nx.is_strongly_connected(graph)) print('число сильно связных компонентов в исходном графе = ', nx.number_strongly_connected_components(graph)) print('Сильно связные компоненты = ', max(nx.strongly_connected_components(graph), key=len)) print('\nИсходный граф является слабо связным?', nx.is_weakly_connected(graph)) print('число слабосвязных компонентов в исходном графе = ', nx.number_weakly_connected_components(graph)) print('Слабо связные компоненты ', max(nx.weakly_connected_components(graph), key=len)) Наконец, определим в рассматриваемом графе пользовательского движения по веб-сайту, кратчайший путь с отдельной страницы блога на конкретную страницу курса. А также определим общее количество этих переходов за сутки (сумма кликов) из этого взвешенного пути, используя алгоритм Дейкстры, о котором мы писали здесь.
length, path = nx.single_source_dijkstra(graph, source='Blog_Page_1', target='COURSE_4') print('Вес пути (число кликов) из страницы блога Blog_Page_1 на страницу курса COURSE_4 = ', length) print('Путь из страницы блога Blog_Page_1 на страницу курса COURSE_4: ', path) С практической точки зрения рассмотренные приемы анализа пользовательских переходов по страницам сайта пригодятся для увеличения вовлеченности клиента (рост длительности сессии), а также помогут оптимизировать путь клиента к конверсионным целям. В частности, поставить на некоторых информационных страницах сайта (страницы блога) баннеры с перелинковкой на страницы продукта (образовательного курса), формы обратной связи для отправки заявки и прочие мероприятия, направленные на рост конверсии.
Подобный пример использования библиотеки NetworkX в продуктовых исследованиях смотрите в наших новых статьях, здесь, здесь и здесь. А какой веб-сервис можно применять для легковесной визуализации данных без написания код, вы узнаете в этом материале.
Подсчитать количество компонент связности графа
В первой строчке выходного файла выведите количество компонент связности. Далее выведите сами компоненты связности в следующем формате: в первой строке количество вершин в компоненте, во второй — сами вершины в порядке возрастания.
Пример:
Входные данные:
6 4
3 1
1 2
5 4
2 3
Выходные данные:
3
3
1 2 3
2
4 5
1
6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
#include #include #include using namespace std; vectorvectorint>> connectedComponents(const vectorvectorint>>& a) { int n = a.size(); vectorbool> mark(n, false); vectorvectorint>> res; for (int i = 0; i n; ++i) { if (mark[i] == false) { mark[i] = true; vectorint> cur; cur.push_back(i); queueint> q; q.push(i); while (!q.empty()) { int x = q.front(); q.pop(); for (int i = 0; i a[x].size(); ++i) { int c = a[x][i]; if (mark[c]) { continue; } mark[c] = true; q.push(c); cur.push_back(c); } } res.push_back(cur); } } return res; } int main() { int n, m; cin >> n >> m; vectorvectorint>> a(n, vectorint>()); for (int i = 0; i m; ++i) { int x,y; cin >> x >> y; --x; --y; a[x].push_back(y); a[y].push_back(x); } auto r = connectedComponents(a); cout size () ; for (int i = 0; i r.size(); ++i) { cout [ i].size() ; for (int j = 0; j r[i].size(); ++j) { cout [ i][j] + 1 <" "; } cout ; } return 0; }