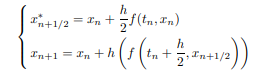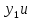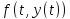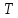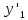Численное решение задачи коши методом эйлера python

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

Differential Equations Course Assignment

mdmxfry/DE-methods

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Variant 19 (Sukach Maxim, BS17-03)

В итоге, наше решение принимает вид:

Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.

Для вычисления используются следующие формулы:

def next_y(xi, yi): return yi + self.h * self.f(xi, yi) ys = [] xs = np.arange(x0 + h, xf + h, h) # вектор всех значений x for x in xs: ys.append(y) y = next_y(x, y) # В результате ys будет содержать все значения метода Эйлера 

Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Усовершенствованный метод Эйлера

Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.

Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:

# Заменяем next_y функцию на эту: def next_y(xi, yi): h2 = h / 2 delta_y = h * f(xi + h2, yi + h2 * f(xi, yi)) return yi + delta_y 

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1

Классический метод Рунге-Кутты

Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.

# Заменяем next_y функцию на эту: def next_y(xi, yi): h2 = h / 2 k1 = f(xi, yi) k2 = f(xi + h2, yi + h2 * k1) k3 = f(xi + h2, yi + h2 * k2) k4 = f(xi + h, yi + h * k3) return yi + (h / 6) * (k1 + 2 * k2 + 2 * k3 + k4) 

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Сравнение методов для заданной задачи

Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1

Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.

График глобальной средней ошибки

Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9

1. Установить Python3
2. Все пакеты необходимые для работы находятся в requirements.txt matplotlib
   numpy
3. Запустить run.py в корневой директории проекта.

Все настройки находятся в run.py в виде констант (строки 12-16). configparser очень не хотелось подключать. После запуска скрипт покажет 6 графиков (в диком разрешении, там ничего не видно толком) и сохранит их нормальные версии (dpi=300) в папке results.

Latex Редактор: https://www.codecogs.com/latex/eqneditor.php
Метод Эйлера: Wikipedia
Усовершенствованный метод Эйлера: Mathprofi (кык)
Метод Рунге — Кутты: Wikipedia

About

Differential Equations Course Assignment

Источник

Решить дифференциальное уравнение методом Эйлера и Эйлера-Коши

Решить дифференциальное уравнение методами Эйлера, Эйлера-Коши, Рунге-Кутта
Помогите решить дифференциальное уравнение Методами Эйлера, Эйлера-Коши, Рунге-Кутта. Y’ = e^2x.

Написать программу которая решает дифференциальное уравнение методом Эйлера и Эйлера-Коши
Написать программу которая решает дифференциальное уравнение методом Эйлера и Эйлера-Коши y’.

Решить дифференциальное уравнение методами эйлера-коши с итерациями и рунге-кутта
решить методами эйлера-коши с итерациями и рунге -куты четвертого порядка диф. уравнение .

Сообщение было отмечено mik-a-el как решение

Решение

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

import numpy as np def function(xy): x, y = map(float, xy.tolist()) return x + np.cos(y/3) y0 = 4.6 h = 0.1 t = [1.6 + i/10 for i in range(11)] print('Метод Эйлера') def euler(xy, h = 0.1, n = 10000): x = xy[0] xy[0] = 0. while x - xy[0] > 0: xy = xy + np.array([h, h * function(xy)]) return xy for x in t : fxy = np.array([x,y0]) print('x = y = '.format(*map(float, euler(fxy, h).tolist()))) print() print('Метод Хойна ') def Heun(xy, h = 0.1, n = 10000): x = xy[0] xy[0] = 0. while x - xy[0] > 0: s1 = function(xy) xy2 = xy + np.array([h, h * s1]) s2 = function(xy2) xy = xy + np.array([h, h * (s1 + s2) / 2]) return xy for x in t : fxy = np.array([x,y0]) print('x = y = '.format(*map(float, Heun(fxy, h).tolist()))) print() print('Метод Рунге — Кутты') def RK4(xy, h = 0.1, n = 10000): x = xy[0] xy[0] = 0. while x - xy[0] > 0: k1 = function(xy) xy2 = xy + np.array([h/2, h/2 * k1]) k2 = function(xy2) xy3 = xy + np.array([h/2, h/2 * k2]) k3 = function(xy3) xy4 = xy + np.array([h, h * k3]) k4 = function(xy4) xy = xy + np.array([h, h * (k1 + 2*(k2 + k3) + k4) / 6]) return xy for x in t : fxy = np.array([x,y0]) print('x = y = '.format(*map(float, RK4(fxy, h).tolist())))

Источник

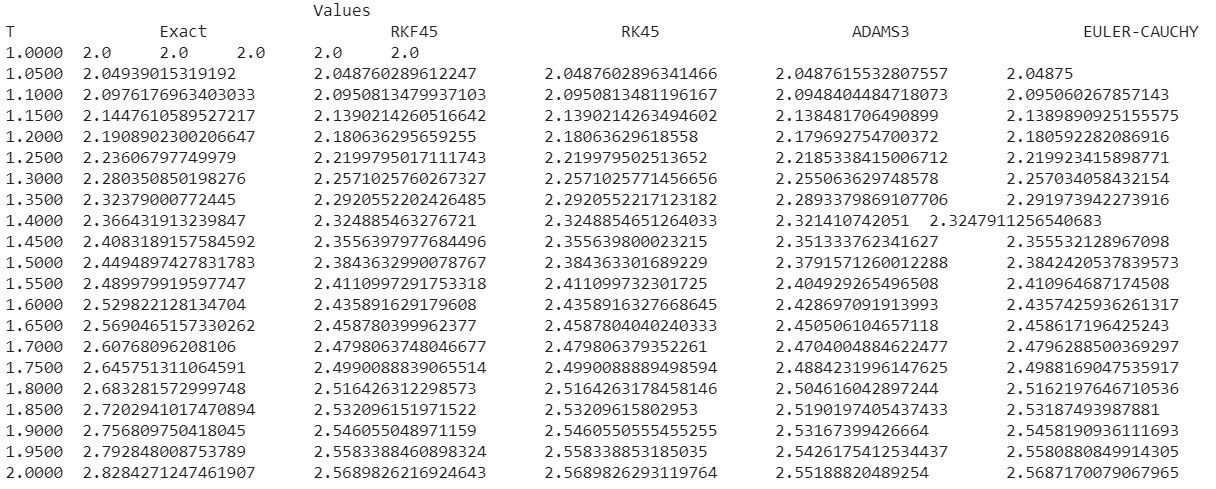
Задание

к системе двух дифференциальных уравнений первого порядка.

Точное решение: y(t)=

Диапазон для t: [1,2].

Решать с шагом h, используя:

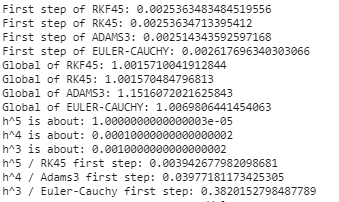
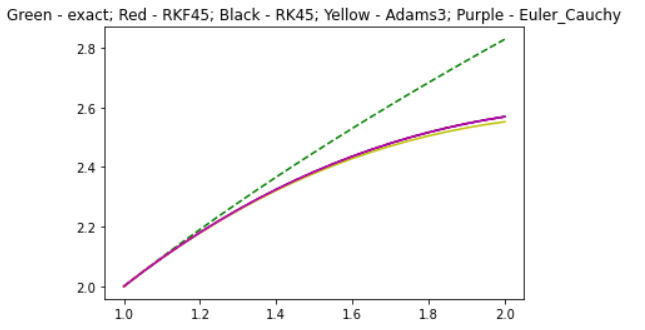
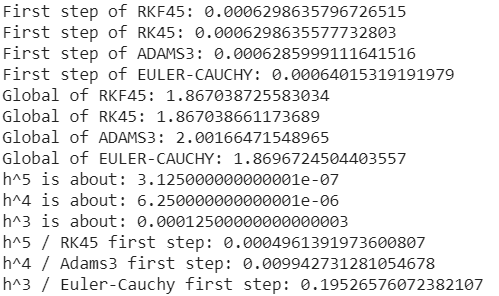
1. программу RKF45
2. метод Эйлера-Коши
3. метод Адамса 3й степени точности
4. метод Рунге-Кутты 4й степени точности

Метод решения

Код программы будем писать на языке Python. Для начала приведем уравнение к системе дифференциальных уравнений первого порядка. Затем проведем вычисления, используя программу RKF45, используя библиотеку SciPy. Далее посчитаем то же самое остальными методами, которые были написаны самостоятельно. Метод Адамса для старта использует метод RK4. Т.к. метод Адамса не самостартующий, для преодоления больших погрешностей, перед началом работы мы, с помощью функции RK4 просчитываем значения 2 точек левее точки старта и саму точку старта. Затем уже, на основании этих данных, вычисляются с большей точностью дальнейшие точки. Расчетные соотношения для метода Эйлера-Коши: Для метода Адамса 3й степени точности: Для метода Рунге-Кутты 4го порядка: Произведя расчеты, получим систему дифференциальных уравнений первого порядка: Для выполнения задания был использован язык Python и следующие библиотеки: Функция pick_step возвращает массив точек t и точных значений в этих точках y(t): Функция f (t, y(t)). В массиве Y хранятся начальные условия и , в массиве dY — значения на нулевой и первой позиции соответственно. Функция, вычисляющая точное решение системы: Первый способ решения. Программа rkf45 с шагом печати h_print = 0.1 и погрешностью atol = 0.0001. Интегрирование осуществляется при помощи функции , которая возвращает настраиваемый объект, при помощи которого можно решать произвольные системы . Этот объект нужно настроить на использование методов Рунге-Кутта при помощи параметра . Соответственно, можно вызвать в некоторой точке для того, чтобы вычислить значение исследуемой функции в ней. Функция rkf45 принимает в качестве параметров , набор точек , в которых нужно вычислить значения и начальные условия . Результатом является массив значений в точках . Второй способ. Метод Рунге-Кутты 4 степени. В двумерном массиве Y содержатся попарно значения в соответствующих точках. В массиве Y0 хранятся начальные условия. Третий способ. Метод Адамса 3 степени точности Суть методов Адамса в пошаговом вычислении значений решения y = y(t) дифференциального уравнения вида y’ = f (t, y). Использование трёх точек и полинома 2-й степени приведёт к формуле, представленной в расчетных соотношениях в начале отчета. Данный метод имеет 3-ю степень точности и является явным. Методы Адамса не являются самостартующими, т. е. они требуют для начала интегрирования специальных стартовых алгоритмов для расчета дополнительных начальных условий. В двумерном массиве Y хранятся значения функции и производные . Чтобы вычислить начальные условия для «старта» метода Адамса, был использован метод Рунге-Кутты 4 степени. С его помощью были получены значения функции f в точках 0.8 и 0.9. Они были сохранены на нулевую и первую позицию массива Y, на второй позиции — начальное условие для точки 1.0. Затем была применена сама формула для вычисления интеграла. Значения в точках 0.8 и 0.9 не относятся к нужному промежутку решений [1;2], поэтому значения из Y были перезаписаны в Y2, начиная с 3 элемента. Четвертый способ. Метод Эйлера-Коши. Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой (y) и независимой (x) переменных между узлами равномерной сетки. Главная функция, запускающая все методы и строящая графики: Результаты Для шага 0.1: Для шага 0.05: Для шага 0.025 Для шага 0.0125 Список конкретных значений слишком велик, я его опущу. Вывод В ходе данной работы были получены решения исходного дифф.уравнения в различных точках с помощью 4-х методов на интервале [1;2]. Решения, полученные с помощью программы rkf45, метода Рунге-Кутты 4 степени и метода Эйлера-Коши оказались самыми точными, однако при уменьшении шага итерирования метод Адамса приблизился к ним по точности.

Источник