Casual impact in python

Measure Causal Impact from GSC Data Using Python

Causal Impact is a Bayesian-like statistical algorithm pioneered by Kay Brodersen working at Google that aims to predict the counterfactual after an event. Take for example you make a large SEO change to a website. Sometimes it’s not obvious whether or not the change was beneficial. You can compare against the past, but the past is the past. What if you could train a model to predict the metric outcome alongside what actually happened. You could then measure the difference! Bingo! The difference is the causal impact.

An obvious observation might be, why wouldn’t you just run an experiment. You could and maybe should, but there are many instances where an experiment may not be possible or perhaps you just forgot or don’t have the time. This method may allow you to give statistical weight to your changes or perhaps the counter.

Causual Impact has deep roots in Causal inference, machine learning, and other statistical topics that are well beyond my grasp so I won’t even try to explain the methods used by the algorithm. Quite frankly it’s a bit of magic to me. The 10k foot view is that you train a model based on a set of time-series data that has one or more control groups. A control group will be a set of relevant data that wouldn’t have been affected by the change (in this script’s case, we’re using historical data as the control). You could even use weather or stock market data if relevant. You set the pre-period range and the post-period range and then using some statistical magic the algorithm predicts the outcome if the change hadn’t occurred.

I strongly suggest reading some of the support material below first to grasp a better understanding of how this all works so you can be more confident looking at the result data. The script is dead simple. The challenge is understanding the results and setting up the data for confidence in those results. Let’s start!

Intro Resources

Two possible modules, the first is what we use in this tutorial and app, but the second is a bit newer and uses TensorFlow Probability on top of the Causal Impact algorithm. Try it out and let me know how it goes!

Requirements and Assumptions

• Python 3 is installed and basic Python syntax understood
• Access to a Linux installation (I recommend Ubuntu) or Google Colab.
• Google Search Console ‘Date’ CSV of your site

Import and Install Modules

• pandas: for importing the GSC CSV file
• causalimpact : handles all the model work and output

First, we need to install causalimpact, from your terminal or Google Colab (include an exclamation mark)

pip3 install pycausalimpact

Now let’s import the two required modules into our script.

import pandas as pd from causalimpact import CausalImpact

Time to import that Date CSV file from Google Search Console. When you export GSC performance data, you’ll download a zip file. Dates CSV file is in it.

• usecols: select the first two columns which happen to be date and clicks.
• header: CSV does not contain a header row
• encoding: BOM(Byte order mark)
• index_col: date column to be used as the index

data = pd.read_csv('Dates.csv', usecols=[0,1], header=0, encoding="utf-8-sig", index_col='Date')

Next, we specify our pre-period and post-period ranges. The time before and after changes have been made. You’ll want both ranges to be equidistant. Note that the success of the prediction sometimes rests on the length of the ranges. Sometimes a shorter range works better, sometimes a longer range. You’ll have to do a little trial and error. The ranges obviously have to exist within the data you upload.

pre_period = ["2020-07-07", "2020-07-13"] # dates prior to change post_period = ["2020-07-14", "2020-07-21"] # dates after change

Now we feed the main CausalImpact() function with our click data and the two ranges. This does all the heavy lifting. Easy!

If you want to add an element of seasonality to the model you can add the attribute nseasons=[] after post_period where X is a number of days. If you have week-day seasonality you could choose the number 7.

ci = CausalImpact(data['Clicks'], pre_period, post_period)

Depending on your data size it can take several seconds to a few minutes to process. Once done all is left is to print out the results.

• summary(): Returns the numerical results in a table form
• plot(): Returns the 3 graphs
  • Predicted: Shows the actual data alongside the predicted outcome from the model
  • PointWise: This shows the difference
  • Cumulative: This shows the summation of difference over time

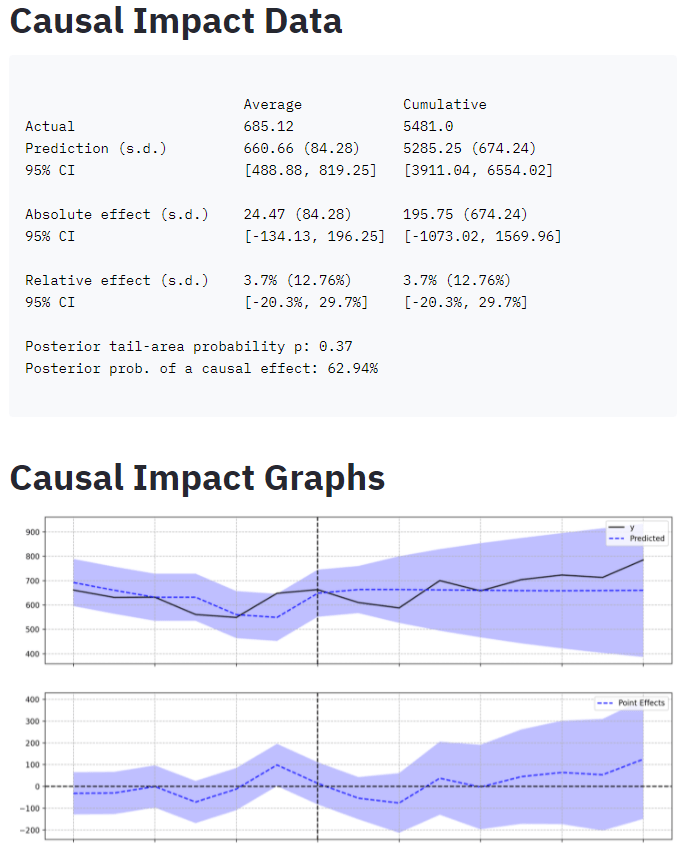
  print(ci.summary()) ci.plot() print(ci.summary(output='report'))

  Translating the Results

  It’s important to understand the algorithm creates many models and stores the results as a distribution. The following data is the analysis of that distribution result.

  Average: The average metric calculated from all the created models
  Cumulative: The summation of all data points for the models

  Actual: The average after-event data (per day) that was provided showing the actual result
  Prediction (s.d.): The mean result data generated by the models. Data if change never happened.
  95% CI (confidence interval): 95% of the models returned a result within this range. The lowest data result from all models and the highest. The prediction will end up being the mean.

  Absolute effect (s.d.): The difference between the actual and the prediction.
  95% CI: 95% of the models returned a difference within this range.

  Relative effect (s.d.): This will be the percent difference
  95% CI: 95% of the models returned a percent difference within this range.

  Posterior tail-area probability p: Likelihood of the result being the result of random fluctuations. Lower the better.
  Posterior prob. of a causal effect: The probability the result is due to a causal effect. Higher the better.

  Conclusion

  Now get out there and try it out! Follow me on Twitter and let me know your applications and ideas!

  

  Acknowledgments

  “CausalImpact 1.2.7, Brodersen et al., Annals of Applied Statistics (2015). https://google.github.io/CausalImpact/”

  Andrea Volpini – WordLift CEO, for his code insight and concept guidance!

  Источник

  Saved searches

  Use saved searches to filter your results more quickly

  You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

  Python Causal Impact Implementation Based on Google’s R Package. Built using TensorFlow Probability.

  License

  WillianFuks/tfcausalimpact

  This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

  Name already in use

  A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

  Sign In Required

  Please sign in to use Codespaces.

  Launching GitHub Desktop

  If nothing happens, download GitHub Desktop and try again.

  Launching GitHub Desktop

  If nothing happens, download GitHub Desktop and try again.

  Launching Xcode

  If nothing happens, download Xcode and try again.

  Launching Visual Studio Code

  Your codespace will open once ready.

  There was a problem preparing your codespace, please try again.

  Latest commit

  Git stats

  Files

  Failed to load latest commit information.

  README.md

  Google’s Causal Impact Algorithm Implemented on Top of TensorFlow Probability.

  The algorithm basically fits a Bayesian structural model on past observed data to make predictions on what future data would look like. Past data comprises everything that happened before an intervention (which usually is the changing of a variable as being present or not, such as a marketing campaign that starts to run at a given point). It then compares the counter-factual (predicted) series against what was really observed in order to extract statistical conclusions.

  Running the model is quite straightforward, it requires the observed data y , covariates X that helps the model through a linear regression, a pre-period interval that selects everything that happened before the intervention and a post-period with data after the «impact» happened.

  Please refer to this medium post for more on this subject.

  pip install tfcausalimpact 

  • python
  • matplotlib
  • jinja2
  • tensorflow>=2.10.0
  • tensorflow_probability>=0.18.0
  • pandas >= 1.3.5

  We recommend this presentation by Kay Brodersen (one of the creators of the Causal Impact in R).

  We also created this introductory ipython notebook with examples of how to use this package.

  This medium article also offers some ideas and concepts behind the library.

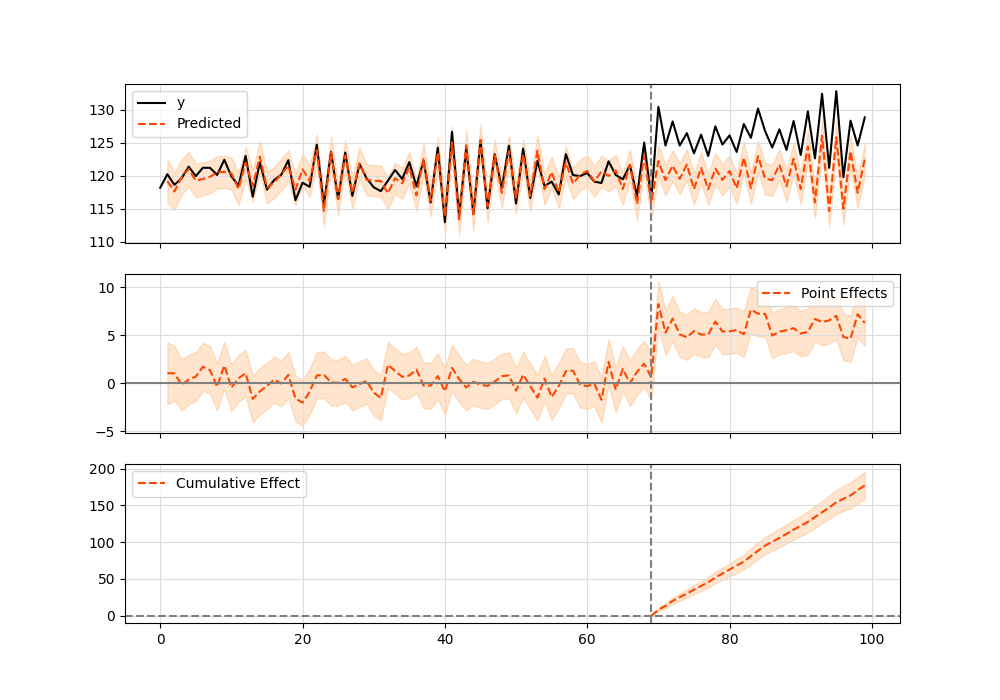
  Here’s a simple example (which can also be found in the original Google’s R implementation) running in Python:

  import pandas as pd from causalimpact import CausalImpact data = pd.read_csv('https://raw.githubusercontent.com/WillianFuks/tfcausalimpact/master/tests/fixtures/arma_data.csv')[['y', 'X']] data.iloc[70:, 0] += 5 pre_period = [0, 69] post_period = [70, 99] ci = CausalImpact(data, pre_period, post_period) print(ci.summary()) print(ci.summary(output='report')) ci.plot()

  Summary should look like this:

  Posterior Inference Average Cumulative Actual 125.23 3756.86 Prediction (s.d.) 120.34 (0.31) 3610.28 (9.28) 95% CI [119.76, 120.97] [3592.67, 3629.06] Absolute effect (s.d.) 4.89 (0.31) 146.58 (9.28) 95% CI [4.26, 5.47] [127.8, 164.19] Relative effect (s.d.) 4.06% (0.26%) 4.06% (0.26%) 95% CI [3.54%, 4.55%] [3.54%, 4.55%] Posterior tail-area probability p: 0.0 Posterior prob. of a causal effect: 100.0% For more details run the command: print(impact.summary('report')) 

  And here’s the plot graphic:

  

  Google R Package vs TensorFlow Python

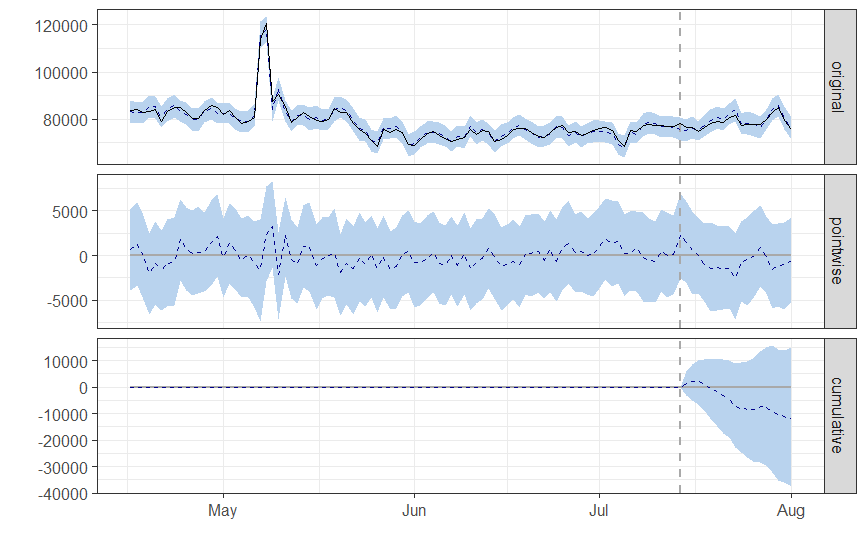
  Both packages should give equivalent results. Here’s an example using the comparison_data.csv dataset available in the fixtures folder. When running CausalImpact in the original R package, this is the result:

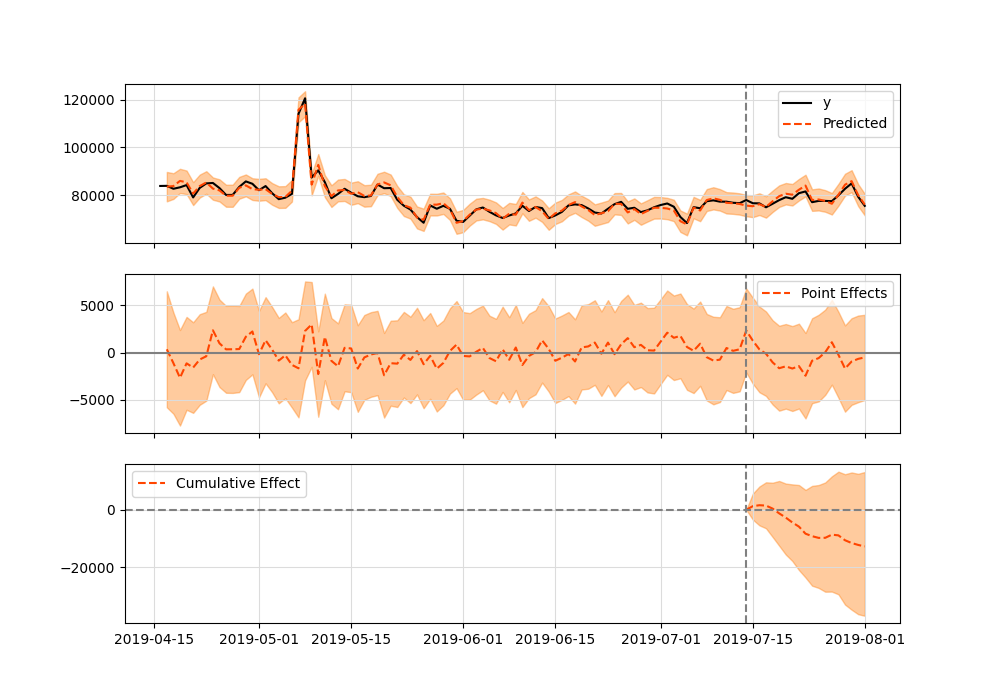
  data = read.csv.zoo('comparison_data.csv', header=TRUE) pre.period  

  Posterior inference Average Cumulative Actual 78574 1414340 Prediction (s.d.) 79232 (736) 1426171 (13253) 95% CI [77743, 80651] [1399368, 1451711] Absolute effect (s.d.) -657 (736) -11831 (13253) 95% CI [-2076, 832] [-37371, 14971] Relative effect (s.d.) -0.83% (0.93%) -0.83% (0.93%) 95% CI [-2.6%, 1%] [-2.6%, 1%] Posterior tail-area probability p: 0.20061 Posterior prob. of a causal effect: 80% For more details, type: summary(impact, "report") 

  

  import pandas as pd from causalimpact import CausalImpact data = pd.read_csv('https://raw.githubusercontent.com/WillianFuks/tfcausalimpact/master/tests/fixtures/comparison_data.csv', index_col=['DATE']) pre_period = ['2019-04-16', '2019-07-14'] post_period = ['2019-7-15', '2019-08-01'] ci = CausalImpact(data, pre_period, post_period, model_args='fit_method': 'hmc'>)

  Posterior Inference Average Cumulative Actual 78574.42 1414339.5 Prediction (s.d.) 79282.92 (727.48) 1427092.62 (13094.72) 95% CI [77849.5, 80701.18][1401290.94, 1452621.31] Absolute effect (s.d.) -708.51 (727.48) -12753.12 (13094.72) 95% CI [-2126.77, 724.92] [-38281.81, 13048.56] Relative effect (s.d.) -0.89% (0.92%) -0.89% (0.92%) 95% CI [-2.68%, 0.91%] [-2.68%, 0.91%] Posterior tail-area probability p: 0.16 Posterior prob. of a causal effect: 84.12% For more details run the command: print(impact.summary('report')) 

  

  Both results are equivalent.

  This package uses as default the Variational Inference method from TensorFlow Probability which is faster and should work for the most part. Convergence can take somewhere between 2~3 minutes on more complex time series. You could also try running the package on top of GPUs to see if results improve.

  If, on the other hand, precision is the top requirement when running causal impact analyzes, it's possible to switch algorithms by manipulating the input arguments like so:

  ci = CausalImpact(data, pre_period, post_period, model_args='fit_method': 'hmc'>)

  This will make usage of the algorithm Hamiltonian Monte Carlo which is State-of-the-Art for finding the Bayesian posterior of distributions. Still, keep in mind that on complex time series with thousands of data points and complex modeling involving various seasonal components this optimization can take 1 hour or even more to complete (on a GPU). Performance is sacrificed in exchange for better precision.

  If you find bugs or have any issues while running this library please consider opening an Issue with a complete description and reproductible environment so we can better help you solving the problem.

  About

  Python Causal Impact Implementation Based on Google's R Package. Built using TensorFlow Probability.

  Источник