Binary value in java

Decimal to Binary in Java

In this tutorial, we will learn how to convert a decimal number to binary in Java. We will see 5 different ways to convert decimal to binary in Java.

Decimal and Binary Numbers

Decimal Numbers

A decimal number is a number that is based on the number 10. In our daily use of numbers, we use decimal numbers. For example, 1234 is a decimal number.

A decimal number includes digits from 0 to 9. The decimal number system is also called the base-10 number system.

Binary Numbers

A binary number is a number that is based on the number 2. In the binary number system, we use only 0 and 1. For example, 1010 is a binary number.

A binary number system is also called the base-2 number system. The binary number system is used in computers and other electronic devices.

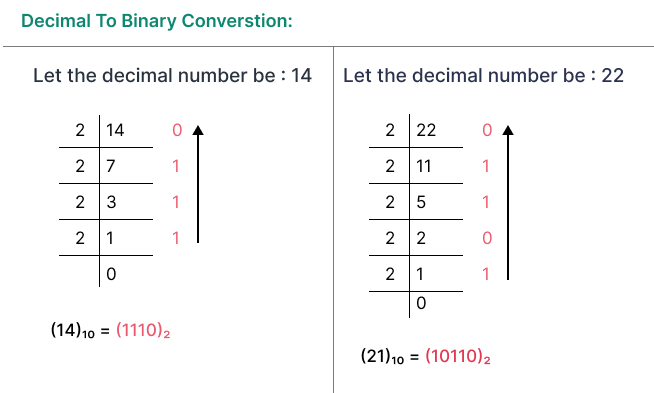
Decimal to Binary Conversion

We can represent a decimal number in a binary number system. For example:

(0)10 = (0)2 (1)10 = (1)2 (2)10 = (10)2 (5)10 = (111)2 (10)10 = (1010)2 (15)10 = (1111)2 (50)10 = (110010)2 (100)10 = (1100100)2

To convert a decimal number to binary, we need to divide the decimal number by 2. The remainder of the division is the binary digit. We continue dividing the quotient by 2 until the quotient is 0 and write the remainder in reverse order.

# Method 1: Print Binary Number Using Array

Here is the first method to convert decimal to binary in Java. In this method, we will use an array to store the remainders.

Algorithm

1. Take the decimal number as input.
2. Divide the decimal number by 2 and store the remainder in an array.
3. Repeat step 2 until the quotient is 0.
4. Print the array in reverse order.

import java.util.Scanner; public class DecimalToBinary < public static void main(String[] args) < // User input Scanner sc = new Scanner(System.in); System.out.print("Enter a decimal number: "); int num = sc.nextInt(); sc.close(); // Solution // initialize an array to store binary number int[] binaryNum = new int[100]; // counter for binary array int i = 0; while (num >0) < // storing remainder in binary array binaryNum[i] = num % 2; num = num / 2; i++; >// printing binary array in reverse order System.out.print("Binary number: "); for (int j = i - 1; j >= 0; j--) < System.out.print(binaryNum[j]); >> >

Enter a decimal number: 10 Binary number: 1010

# Method 2: Return Binary Number as String

In this method, we will create a function that will take a decimal number as input and return the binary number as output.

We will return the binary number as a string.

Algorithm

1. The method takes a decimal number as input.
2. Initialize an empty string to store the binary number.
3. Divide the decimal number by 2 and store the remainder in the string. Make sure to add the remainder to the beginning of the string.
4. Repeat step 3 until the quotient is 0.
5. Return the binary number as a string.

import java.util.Scanner; public class DtoB < public static String decimalToBinary(int decimal) < String binary = ""; while (decimal >0) < binary = (decimal % 2) + binary; decimal = decimal / 2; >return binary; > public static void main(String[] args) < // User input Scanner sc = new Scanner(System.in); System.out.print("Enter a decimal number: "); int num = sc.nextInt(); sc.close(); // call the method String bin = decimalToBinary(num); System.out.println("Binary number: " + bin); >>

Enter a decimal number: 25 Binary number: 11001

# Method 3: Return Binary Number as Integer Using Array

In this method, we will use an array to store the binary digits. We will reverse the array to get the correct binary number.

import java.util.Scanner; public class DtoB < public static int decimalToBinary(int decimal) < int[] binary = new int[100]; int i = 0; while (decimal >0) < binary[i] = decimal % 2; decimal = decimal / 2; i++; >int bin = 0; for (int j = i - 1; j >= 0; j--) < bin = bin * 10 + binary[j]; >return bin; > public static void main(String[] args) < // User input Scanner sc = new Scanner(System.in); System.out.print("Enter a decimal number: "); int num = sc.nextInt(); sc.close(); // call the method int bin = decimalToBinary(num); System.out.println("Binary number: " + bin); >>

Enter a decimal number: 50 Binary number: 110010

Note : Maximum value of an integer in Java is 2,147,483,647. If the binary number is greater than this value, it will give an incorrect output. To increase the maximum value of an integer, we can use the long data type.

# Method 4: Return Binary Number as Integer Without Using Array

In this method, we will create a function that will convert a decimal number to a binary number and return the binary number as an integer.

Binary digits need to reverse to get the correct binary number. So we store each bit in an array and reverse it later.

But in this method, we will not use an array.

import java.util.Scanner; public class DtoB < public static int decimalToBinary(int decimal) < int binary = 0; int i = 0; while (decimal >0) < binary = binary + (decimal % 2) * (int) Math.pow(10, i); decimal = decimal / 2; i++; >return binary; > public static void main(String[] args) < // User input Scanner sc = new Scanner(System.in); System.out.print("Enter a decimal number: "); int num = sc.nextInt(); sc.close(); // call the method int bin = decimalToBinary(num); System.out.println("Binary number: " + bin); >>

Enter a decimal number: 100 Binary number: 1100100

# Method 5: Using Recursive Function

In this method, we will use recursion to convert decimal numbers to binary.

A recursive function is a function that calls itself.

import java.util.Scanner; public class DtoB < public static int decimalToBinary(int decimal) < if (decimal == 0) < return 0; >else < return (decimal % 2) + 10 * decimalToBinary(decimal / 2); >> public static void main(String[] args) < // User input Scanner sc = new Scanner(System.in); System.out.print("Enter a decimal number: "); int num = sc.nextInt(); sc.close(); // call the method int bin = decimalToBinary(num); System.out.println("Binary number: " + bin); >>

Enter a decimal number: 30 Binary number: 11110

Источник

Binary Literals

In Java SE 7, the integral types ( byte , short , int , and long ) can also be expressed using the binary number system. To specify a binary literal, add the prefix 0b or 0B to the number. The following examples show binary literals:

// An 8-bit 'byte' value: byte aByte = (byte)0b00100001; // A 16-bit 'short' value: short aShort = (short)0b1010000101000101; // Some 32-bit 'int' values: int anInt1 = 0b10100001010001011010000101000101; int anInt2 = 0b101; int anInt3 = 0B101; // The B can be upper or lower case. // A 64-bit 'long' value. Note the "L" suffix: long aLong = 0b1010000101000101101000010100010110100001010001011010000101000101L;

Binary literals can make relationships among data more apparent than they would be in hexadecimal or octal. For example, each successive number in the following array is rotated by one bit:

public static final int[] phases =

In hexadecimal, the relationship among the numbers is not readily apparent:

public static final int[] phases =

You can use binary integral constants in code that you can verify against a specifications document, such as a simulator for a hypothetical 8-bit microprocessor:

public State decodeInstruction(int instruction, State state) < if ((instruction & 0b11100000) == 0b00000000) < final int register = instruction & 0b00001111; switch (instruction & 0b11110000) < case 0b00000000: return state.nop(); case 0b00010000: return state.copyAccumTo(register); case 0b00100000: return state.addToAccum(register); case 0b00110000: return state.subFromAccum(register); case 0b01000000: return state.multiplyAccumBy(register); case 0b01010000: return state.divideAccumBy(register); case 0b01100000: return state.setAccumFrom(register); case 0b01110000: return state.returnFromCall(); default: throw new IllegalArgumentException(); >> else < final int address = instruction & 0b00011111; switch (instruction & 0b11100000) < case 0b00100000: return state.jumpTo(address); case 0b01000000: return state.jumpIfAccumZeroTo(address); case 0b01000000: return state.jumpIfAccumNonzeroTo(address); case 0b01100000: return state.setAccumFromMemory(address); case 0b10100000: return state.writeAccumToMemory(address); case 0b11000000: return state.callTo(address); default: throw new IllegalArgumentException(); >> >

You can use binary literals to make a bitmap more readable:

public static final short[] HAPPY_FACE =

Источник

Двоичные числа в Java

Двоичная система счисления использует 0 и 1 для представления чисел. Компьютеры используют двоичные числа для хранения и выполнения операций над любыми данными.

В этом уроке мы узнаем, как преобразовать двоичное число в десятичное и наоборот. Кроме того, мы будем выполнять сложение и вычитание на них.

2. Двоичный литерал​

Java 7 представила двоичный литерал. Это упростило использование двоичных чисел.

Чтобы использовать его, нам нужно добавить к номеру префикс 0B или 0b:

 @Test   public void given_binaryLiteral_thenReturnDecimalValue()     byte five = 0b101;   assertEquals((byte) 5, five);    short three = 0b11;   assertEquals((short) 3, three);    int nine = 0B1001;   assertEquals(9, nine);    long twentyNine = 0B11101;   assertEquals(29, twentyNine);    int minusThirtySeven = -0B100101;   assertEquals(-37, minusThirtySeven);    > 

3. Преобразование двоичных чисел​

В этом разделе мы узнаем, как преобразовать двоичное число в его десятичный формат и наоборот. Здесь мы сначала воспользуемся встроенной функцией Java для преобразования, а затем напишем для нее собственные методы.

3.1. Десятичное число в двоичное​

Integer имеет функцию toBinaryString для преобразования десятичного числа в двоичную строку:

 @Test   public void given_decimalNumber_then_convertToBinaryNumber()    assertEquals("1000", Integer.toBinaryString(8));   assertEquals("10100", Integer.toBinaryString(20));   > 

Теперь мы можем попробовать написать собственную логику для этого преобразования. Прежде чем писать код, давайте сначала разберемся, как преобразовать десятичное число в двоичное.

Чтобы преобразовать десятичное число n в его двоичный формат, нам нужно:

1. Разделите n на 2, учитывая частное q и остаток r
2. Разделите q на 2, заметив частное и остаток.
3. Повторяем шаг 2, пока не получим 0 в качестве частного
4. Объединить в обратном порядке все остатки

Давайте посмотрим на пример преобразования 6 в эквивалент двоичного формата:

1. Сначала разделите 6 на 2: частное 3, остаток 0
2. Затем разделите 3 на 2: частное 1, остаток 1.
3. И, наконец, разделите 1 на 2: частное 0, остаток 1
4. 110

Давайте теперь реализуем приведенный выше алгоритм:

 public Integer convertDecimalToBinary(Integer decimalNumber)     if (decimalNumber == 0)    return decimalNumber;   >    StringBuilder binaryNumber = new StringBuilder();   Integer quotient = decimalNumber;    while (quotient > 0)    int remainder = quotient % 2;   binaryNumber.append(remainder);   quotient /= 2;   >    binaryNumber = binaryNumber.reverse();   return Integer.valueOf(binaryNumber.toString());   > 

3.2. Двоичный в десятичное число​

Для разбора двоичной строки класс Integer предоставляет функцию parseInt :

 @Test   public void given_binaryNumber_then_ConvertToDecimalNumber()    assertEquals(8, Integer.parseInt("1000", 2));   assertEquals(20, Integer.parseInt("10100", 2));   > 

Здесь функция parseInt принимает на вход два параметра:

1. Двоичная строка для преобразования
2. Основание или основание системы счисления, в которую необходимо преобразовать входную строку

Теперь давайте попробуем написать нашу собственную логику для преобразования двоичного числа в десятичное:

1. Начать с самой правой цифры
2. Умножьте каждую цифру на 2 ^ этой цифры — здесь позиция самой правой цифры равна нулю, и она увеличивается по мере продвижения влево.
3. Сложите результат всех умножений, чтобы получить окончательное десятичное число

Снова давайте посмотрим на наш метод в действии:

1. Во-первых, 101011 = (12^5) + (02^4) + (12^3) + (02^2) + (12^1) + (12^0) )
2. Далее, 101011 = (132) + (016) + (18) + (04) + (12) + (11)
3. Тогда 101011 = 32 + 0 + 8 + 0 + 2 + 1
4. И, наконец, 101011 = 43.

Давайте, наконец, закодируем вышеуказанные шаги:

 public Integer convertBinaryToDecimal(Integer binaryNumber)     Integer decimalNumber = 0;   Integer base = 1;    while (binaryNumber > 0)    int lastDigit = binaryNumber % 10;   binaryNumber = binaryNumber / 10;   decimalNumber += lastDigit * base;   base = base * 2;   >   return decimalNumber;   > 

4. Арифметические операции​

В этом разделе мы сосредоточимся на выполнении арифметических операций над двоичными числами.

4.1. Добавление​

Как и при сложении десятичных чисел, мы начинаем складывать числа с самой правой цифры.

При сложении двух двоичных цифр нам нужно помнить следующие правила:

Эти правила могут быть реализованы как:

 public Integer addBinaryNumber(Integer firstNum, Integer secondNum)    StringBuilder output = new StringBuilder();   int carry = 0;   int temp;   while (firstNum != 0 || secondNum != 0)    temp = (firstNum % 10 + secondNum % 10 + carry) % 2;   output.append(temp);    carry = (firstNum % 10 + secondNum % 10 + carry) / 2;   firstNum = firstNum / 10;   secondNum = secondNum / 10;   >   if (carry != 0)    output.append(carry);   >   return Integer.valueOf(output.reverse().toString());   > 

4.2. вычитание​

Существует много способов вычитания двоичных чисел. В этом разделе мы изучим метод дополнения до единицы для выполнения вычитания.

Давайте сначала разберемся, что такое дополнение числа.

Дополнением до единицы является число, полученное путем инвертирования каждой цифры двоичного числа. Это означает, что просто замените 1 на 0 и 0 на 1 :

 public Integer getOnesComplement(Integer num)    StringBuilder onesComplement = new StringBuilder();   while (num > 0)    int lastDigit = num % 10;   if (lastDigit == 0)    onesComplement.append(1);   > else    onesComplement.append(0);   >   num = num / 10;   >   return Integer.valueOf(onesComplement.reverse().toString());   > 

Чтобы выполнить вычитание двух двоичных чисел с использованием дополнения до единицы, нам необходимо:

1. Вычислить дополнение вычитаемого s до единицы
2. Добавьте s и минус
3. Если на шаге 2 генерируется перенос, добавьте его к результату шага 2, чтобы получить окончательный ответ.
4. Если перенос не генерируется на шаге 2, то окончательным ответом является дополнение к единице результата шага 2. Но в данном случае ответ отрицательный

Давайте реализуем вышеуказанные шаги:

 public Integer substractBinaryNumber(Integer firstNum, Integer secondNum)    int onesComplement = Integer.valueOf(getOnesComplement(secondNum));   StringBuilder output = new StringBuilder();   int carry = 0;   int temp;   while (firstNum != 0 || onesComplement != 0)    temp = (firstNum % 10 + onesComplement % 10 + carry) % 2;   output.append(temp);   carry = (firstNum % 10 + onesComplement % 10 + carry) / 2;    firstNum = firstNum / 10;   onesComplement = onesComplement / 10;   >   String additionOfFirstNumAndOnesComplement = output.reverse().toString();   if (carry == 1)    return addBinaryNumber(Integer.valueOf(additionOfFirstNumAndOnesComplement), carry);   > else    return getOnesComplement(Integer.valueOf(additionOfFirstNumAndOnesComplement));   >   > 

5. Вывод​

В этой статье мы научились преобразовывать двоичные числа в десятичные и наоборот. Затем мы выполнили арифметические операции, такие как сложение и вычитание над двоичными числами.

Полный код, использованный в этой статье, доступен на GitHub .

Источник