3.7. Dictionaries¶
The second major Python data structure is the dictionary. As you probably recall, dictionaries differ from lists in that you can access items in a dictionary by a key rather than a position. Later in this book you will see that there are many ways to implement a dictionary. The thing that is most important to notice right now is that the get item and set item operations on a dictionary are \(O(1)\) . Another important dictionary operation is the contains operation. Checking to see whether a key is in the dictionary or not is also \(O(1)\) . The efficiency of all dictionary operations is summarized in Table 3 . One important side note on dictionary performance is that the efficiencies we provide in the table are for average performance. In some rare cases the contains, get item, and set item operations can degenerate into \(O(n)\) performance but we will get into that in a later chapter when we talk about the different ways that a dictionary could be implemented.
Table 3: Big-O Efficiency of Python Dictionary Operations ¶
For our last performance experiment we will compare the performance of the contains operation between lists and dictionaries. In the process we will confirm that the contains operator for lists is \(O(n)\) and the contains operator for dictionaries is \(O(1)\) . The experiment we will use to compare the two is simple. We’ll make a list with a range of numbers in it. Then we will pick numbers at random and check to see if the numbers are in the list. If our performance tables are correct the bigger the list the longer it should take to determine if any one number is contained in the list.
We will repeat the same experiment for a dictionary that contains numbers as the keys. In this experiment we should see that determining whether or not a number is in the dictionary is not only much faster, but the time it takes to check should remain constant even as the dictionary grows larger.
Listing 6 implements this comparison. Notice that we are performing exactly the same operation, number in container . The difference is that on line 7 x is a list, and on line 9 x is a dictionary.
1import timeit 2import random 3 4for i in range(10000,1000001,20000): 5 t = timeit.Timer("random.randrange(%d) in x"%i, 6 "from __main__ import random,x") 7 x = list(range(i)) 8 lst_time = t.timeit(number=1000) 9 x = j:None for j in range(i)> 10 d_time = t.timeit(number=1000) 11 print("%d,%10.3f,%10.3f" % (i, lst_time, d_time))
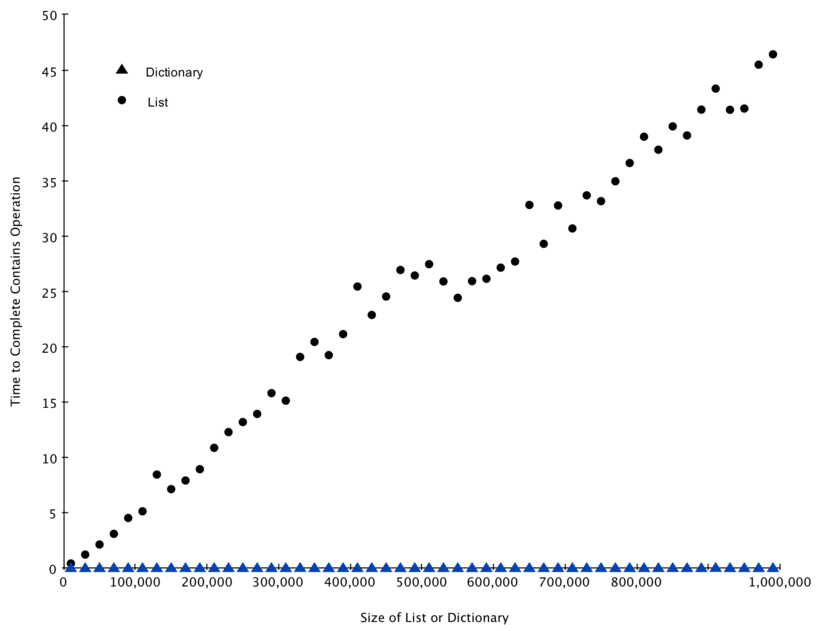
Figure 4 summarizes the results of running Listing 6 . You can see that the dictionary is consistently faster. For the smallest list size of 10,000 elements a dictionary is 89.4 times faster than a list. For the largest list size of 990,000 elements the dictionary is 11,603 times faster! You can also see that the time it takes for the contains operator on the list grows linearly with the size of the list. This verifies the assertion that the contains operator on a list is \(O(n)\) . It can also be seen that the time for the contains operator on a dictionary is constant even as the dictionary size grows. In fact for a dictionary size of 10,000 the contains operation took 0.004 milliseconds and for the dictionary size of 990,000 it also took 0.004 milliseconds.
Since Python is an evolving language, there are always changes going on behind the scenes. The latest information on the performance of Python data structures can be found on the Python website. As of this writing the Python wiki has a nice time complexity page that can be found at the Time Complexity Wiki.
Q-1: Which of the list operations shown below is not O(1)?
Q-2: Which of the dictionary operations shown below is O(1)?
User
This page documents the time-complexity (aka «Big O» or «Big Oh») of various operations in current CPython. Other Python implementations (or older or still-under development versions of CPython) may have slightly different performance characteristics. However, it is generally safe to assume that they are not slower by more than a factor of O(log n).
Generally, ‘n’ is the number of elements currently in the container. ‘k’ is either the value of a parameter or the number of elements in the parameter.
list
The Average Case assumes parameters generated uniformly at random.
Internally, a list is represented as an array; the largest costs come from growing beyond the current allocation size (because everything must move), or from inserting or deleting somewhere near the beginning (because everything after that must move). If you need to add/remove at both ends, consider using a collections.deque instead.
collections.deque
A deque (double-ended queue) is represented internally as a doubly linked list. (Well, a list of arrays rather than objects, for greater efficiency.) Both ends are accessible, but even looking at the middle is slow, and adding to or removing from the middle is slower still.
See dict — the implementation is intentionally very similar.
- As seen in the source code the complexities for set difference s-t or s.difference(t) (set_difference()) and in-place set difference s.difference_update(t) (set_difference_update_internal()) are different! The first one is O(len(s)) (for every element in s add it to the new set, if not in t). The second one is O(len(t)) (for every element in t remove it from s). So care must be taken as to which is preferred, depending on which one is the longest set and whether a new set is needed.
- To perform set operations like s-t, both s and t need to be sets. However you can do the method equivalents even if t is any iterable, for example s.difference(l), where l is a list.
dict
The Average Case times listed for dict objects assume that the hash function for the objects is sufficiently robust to make collisions uncommon. The Average Case assumes the keys used in parameters are selected uniformly at random from the set of all keys.
Note that there is a fast-path for dicts that (in practice) only deal with str keys; this doesn’t affect the algorithmic complexity, but it can significantly affect the constant factors: how quickly a typical program finishes.
Notes
[1] = These operations rely on the «Amortized» part of «Amortized Worst Case». Individual actions may take surprisingly long, depending on the history of the container. [2] = Popping the intermediate element at index k from a list of size n shifts all elements after k by one slot to the left using memmove. n — k elements have to be moved, so the operation is O(n — k). The best case is popping the second to last element, which necessitates one move, the worst case is popping the first element, which involves n — 1 moves. The average case for an average value of k is popping the element the middle of the list, which takes O(n/2) = O(n) operations. [3] = For these operations, the worst case n is the maximum size the container ever achieved, rather than just the current size. For example, if N objects are added to a dictionary, then N-1 are deleted, the dictionary will still be sized for N objects (at least) until another insertion is made.TimeComplexity (last edited 2023-01-19 22:35:03 by AndrewBadr )