Спектральный анализ сигналов нелинейных звеньев АСУ на Python
В моей статье [1] рассмотрен метод гармонической линеаризации для исследования систем управления, содержащих нелинейные элементы.
Этот метод может быть использован в том случае, когда линейная часть системы является низкочастотным фильтром, т.е. отфильтровывает все возникающие на выходе нелинейного элемента гармонические составляющие, кроме первой гармоники [2]. Поэтому логическим продолжением моей первой статьи будет гармонический анализ рассмотренных нелинейных элементов. Кроме этого нужно рассмотреть аппаратную альтернативу методу гармонической линеаризации.
Метод анализа и программный код
Пусть на нелинейные элементы поступает чистый синусоидальный сигнал. Методом разложения в дискретный ряд Фурье получим его спектр.
#!/usr/bin/env python #coding=utf8 from numpy import array, arange, abs as np_abs from numpy.fft import rfft, rfftfreq from math import sin, pi import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.family'] = 'fantasy' mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial' FD = 250000#частота дискретизации, отсчётов в секунду N = 2500#длина входного массива, N/FD секунд F=250.0#циклическая частота входного сигнала w=(2.*pi*F/FD)#отсчёт круговой частоты A=3.0#амплитуда сигнала B=0.5#порог ограничения #сгенерируем чистый синусоидальный сигнал с частотой F длиной N sin_sig = array([A*sin(w*t) for t in range(N)])#график сигнала plt.plot(arange(N)/float(FD), sin_sig, 'r') plt.xlabel('Время, сек.') plt.ylabel('Амплитуда сигнала') plt.title('Входной синусоидальный сигнала') plt.grid(True) plt.show() spectr_sin = rfft(sin_sig )#вычисляем дискретное действительное rfft преобразование Фурье plt.plot(rfftfreq(N, 1./FD), np_abs(spectr_sin)/N) #график спектра plt.xlabel('Частота, Гц') plt.ylabel('Амплитуда сигнала') plt.title('Спектр синусоидального сигнала') plt.grid(True) plt.show() Получим сигнал и спектр сигнала с выхода нелинейного элемента с «насыщением».
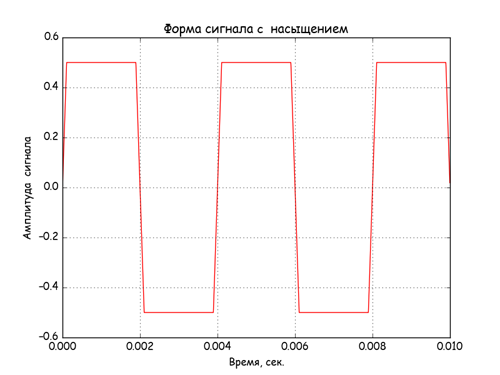
# сгенерируем сигнал нелинейности c «насыщением» из A*sin(w*t) при abs(А)>abs(B) sinp_sig =array([A*sin(w*t) if abs(A*sin(w*t)) Для учёта знака ограничения B использован следующий код — A*sin(w*t)*B/abs(A*sin(w*t).
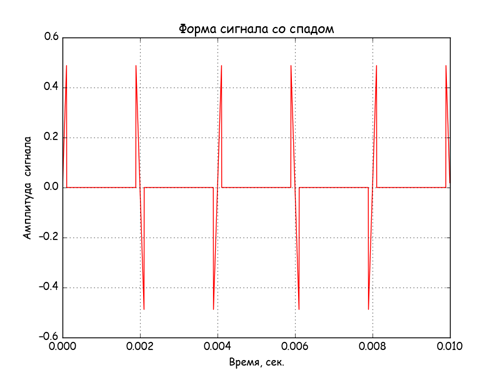
Получим вид сигнала и спектр нелинейного элемента с переходом амплитуды в ноль.
# сгенерируем сигнал нелинейности «cо спадом до нуля» из A*sin(w*t) при abs(А)=abs(B) sinn_sig = array([A*sin(w*t) if abs(A*sin(w*t)) Результаты
Сигнала на входе и на выходе нелинейных элементов.
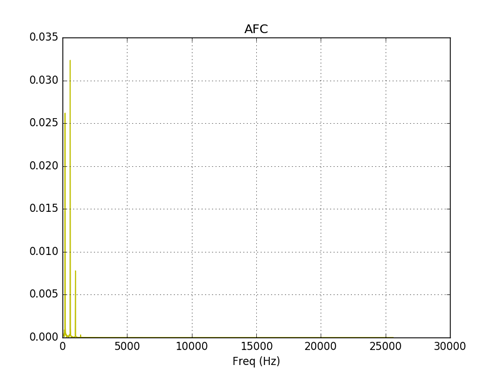
Спектры сигналов на выходе нелинейных элементов.
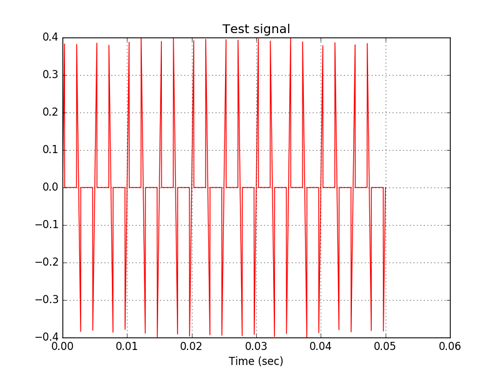
Нелинейный элемент со спадом сигнала генерирует большое число высокочастотных гармоник. Для фильтрации сигнала на выходе нелинейных элементов можно применить цифровой НЧ фильтр, детально описанный в работе [3]. Для исследования возможностей цифровой фильтрации сигналов нелинейных элементов в код программы [3], были внесены следующие изменения.
A=1.0 B=0.4 test_n = 2560 # Кол-во отсчётов тестового сигнала test_f = 200 # Наименьшая отличная от нуля частота тестового сигнала test_period_count = 10.0 # Кол-во периодов тестового сигнала test_t = numpy.linspace(0.0, test_period_count/test_f, test_n) # Базовый сигнал sin(wt), подлежащий восстановлению фильтром test_base_signal = array([A*sin(2*pi*test_f* i) for i in test_t ]) test_signal =array([A*sin(2*pi*test_f* i) if abs(sin(2*pi*test_f* i)) Спектр сигнала на выходе фильтра.
Вывод
Решить задачу использования нелинейных элементов можно аппаратно используя микропроцессор, но при этом необходимо согласование уровней сигналов, а так же ЦАП и АЦП.
О классификации методов преобразования Фурье на примерах их программной реализации средствами Python
Публикации по методу Фурье условно можно разделить на две группы. Первая группа так называемых познавательных публикаций, например, [1,2].
Вторая группа публикаций касается применения преобразований Фурье в технике, например, при спектральном анализе [3,4].
Ни в коем случае не умоляя достоинства этих групп публикации стоит признать, что без классификации, или хотя бы попытки осуществить такую классификацию, получить системное представление о методе Фурье, по моему мнению, затруднительно.
Задачи публикации
Провести классификацию методов преобразования Фурье на примерах их программной реализации средствами Python. При этом для облегчения чтения использовать формулы только в программном коде с соответствующими пояснениями.
Гармонический анализ и синтез
Гармоническим анализом называют разложение функции f(t), заданной на отрезке [0, Т] в ряд Фурье или в вычислении коэффициентов Фурье по формулам.
Гармоническим синтезом называют получение колебаний сложной формы путем суммирования их гармонических составляющих (гармоник).
#!/usr/bin/python # -*- coding: utf-8 -* from scipy.integrate import quad # модуль для интегрирования import matplotlib.pyplot as plt # модуль для графиков import numpy as np # модуль для операций со списками и массивами T=np.pi; w=2*np.pi/T# период и круговая частота def func(t):# анализируемая функция if t=pi f(t)=-cos(t)") plt.plot(q, F1, label='1 гармоника') plt.plot(q, F2 , label='2 гармоника') plt.plot(q, F3, label='3 гармоника') plt.xlabel("Время t") plt.ylabel("Амплитуда А") plt.legend(loc='best') plt.grid(True) F=np.array(a[0]/2)+np.array([0*t for t in q-1])# подготовка массива для анализа с a[0]/2 for k in np.arange(1,c,1): F=F+np.array([a[k]*np.cos(w*k*t)+b[k]*np.sin(w*k*t) for t in q])# вычисление членов ряда Фурье plt.figure() P=[func(t) for t in q] plt.title("Классический гармонический синтез") plt.plot(q, P, label='f(t)') plt.plot(q, F, label='F(t)') plt.xlabel("Время t") plt.ylabel("f(t),F(t)") plt.legend(loc='best') plt.grid(True) plt.show() Результат
Спектральный анализ периодических функций заключается в нахождении амплитуды Аk и фазы j k гармоник (косинусоид) ряда Фурье. Задача, обратная спектральному анализу, называется спектральным синтезом.
Программная реализация для спектрального анализа и синтеза без специальных функций NumPy для Фурье преобразования
#!/usr/bin/python # -*- coding: utf-8 -* from scipy.integrate import quad # модуль для интегрирования import matplotlib.pyplot as plt # модуль для графиков import numpy as np # модуль для операций со списками и массивами T=np.pi; w=2*np.pi/T# период и круговая частота def func(t):# анализируемая функция if t Результат
Программная реализация спектрального анализа и синтеза с использованием функций NumPy прямого быстрого преобразования Фурье – rfft и обратного преобразования – irfft
#!/usr/bin/python # -*- coding: utf-8 -* import matplotlib.pyplot as plt import numpy as np import numpy.fft T=np.pi;z=T/16; m=[k*z for k in np.arange(0,16,1)];arg=[];q=[]# 16 отсчётов на период в пи def f(t):# анализируемая функция if t Фильтрация аналоговых сигналов
Под фильтрацией подразумевается выделение полезного сигнала из его смеси с мешающим сигналом — шумом. Наиболее распространенный тип фильтрации — частотная фильтрация. Если известна область частот, занимаемых полезным сигналом, достаточно выделить эту область и подавить те области, которые заняты шумом.
Программная реализация иллюстрирует технику фильтрации с применением БПФ. Сначала синтезируется исходный сигнал, представленный 128 отсчетами вектора v. Затем к этому сигналу присоединяется шум с помощью генератора случайных чисел (функция np. random.uniform(0,0.5)) и формируется вектор из 128 отсчетов зашумленного сигнала.
#!/usr/bin/python # -*- coding: utf-8 -* import matplotlib.pyplot as plt import numpy as np from numpy.fft import rfft, irfft from numpy.random import uniform k=np.arange(0,128,1) T=np.pi;z=T/128; m=[t*z for t in k]#задание для дискретизации функции на 128 отсчётов def f(t):#анализируемая функция if t=0: q=1 else: q=0 return q v=[f(t) for t in m]#дискретизация исходной функции vs= [f(t)+np.random.uniform(0,0.5) for t in m]# добавление шума plt.figure() plt.title("Фильтрация аналоговых сигналов \n Окно исходной и зашумленной функций") plt.plot(k,v, label='Окно исходной функции шириной pi') plt.plot(k,vs,label='Окно зашумленной функции шириной pi') plt.xlabel("Отсчёты -k") plt.ylabel("Амплитуда А") plt.legend(loc='best') plt.grid(True) al=2# степень фильтрации высших гармоник fs=np. fft.rfft(v)# переход из временной области в частотную с помощью БПФ g=[fs[j]*FH(abs(fs[j])-2) for j in np.arange(0,65,1)]# фильтрация высших гармоник h=np.fft.irfft(g) # возврат во временную область plt.figure() plt.title("Фильтрация аналоговых сигналов \n Результат фильтрации") plt.plot(k,v,label='Окно исходной функции шириной pi') plt.plot(k,h, label='Окно результата фильтрации шириной pi') plt.xlabel("Отсчёты -k") plt.ylabel("Амплитуда А") plt.legend(loc='best') plt.grid(True) plt.show() Результат
Решение дифференциальных уравнений в частных производных
Алгоритм решения дифференциальных уравнений математической физики с использованием прямого и обратного БПФ приведен в [5]. Воспользуемся приведенными данными для программной реализации на Python решения дифференциального уравнения распространения тепла в стержне с применением преобразования Фурье.
#!/usr/bin/env python #coding=utf8 import numpy as np from numpy.fft import fft, ifft # функции быстрого прямого и обратного преобразования Фурье import pylab# модуль построения поверхности from mpl_toolkits.mplot3d import Axes3D# модуль построения поверхности n=50# стержень длиной 2 пи разбивается на 50 точек times=10# количества итераций во времени h=0.01# шаг по времени x=[r*2*np.pi/n for r in np.arange(0,n)]# дискретизация х w= np.fft.fftfreq(n,0.02)# сдвиг нулевой частотной составляющей к центру спектра k2=[ r**2 for r in w]# коэффициенты разложения u0 =[2 +np.sin(i) + np.sin(2*i) for i in x]# дискретизация начального распределения температуры вдоль стержня u = np.zeros([times,n])# матрица нулей размерностью 10*50 u[0,:] = u0 # нудевые начальные условия uf =np.fft. fft(u0) # коэффициенты Фурье начальной функции for i in np.arange(1,times,1): uf=uf*[(1-h*k) for k in k2] #следующий временной шаг в пространстве Фурье u[i,:]=np.fft.ifft(uf).real #до конца физического пространства X = np.zeros([times,n])# подготовка данных координаты х для поверхности for i in np.arange(0,times,1): X[i:]=x T = np.zeros([times,n])# подготовка данных координаты t для поверхности for i in np.arange(0,times,1): T[i:]=[h*i for r in np.arange(0,n)] fig = pylab.figure() axes = Axes3D(fig) axes.plot_surface(X, T, u) pylab.show() Результат
Вывод
В статье приведена попытка классификации по областям применения методов преобразования Фурье.