Алгоритм вычисления суммы чисел программирование

1.2. Алгоритмы вычисления сумм и произведений в цикле

Эффективным средством реализации указанных вычислений является использование циклических вычислительных процессов, но при этом сле­дует соблюдать два правила:

Правило накопления суммы: переменной, с помощью которой будет накапливаться сумма в цикле, необходимо при­своить начальное значение 0 (ноль) до входа в цикл.

Правило накопления произведений: переменной, с помощью которой будет накапливаться произведение в цикле, необходимо присвоить начальное значение 1 (единица) до входа в цикл.

Рассмотрим, чем обусловлены эти два правила.

При вычислении сумм вида (8.5) используется принцип накапливания сумм, реализуемый при помощи рекуррентной формулы вида

где – значение суммы, содержащей k-1 слагаемое; – зна­чение суммы, содержащей k слагаемых; – значение k-го слагаемого.

Использование формулы (8.7) заключается в следующем. Примем на­чальное значение суммы равным нулю: S₀ (при k = 1). Зададим ин­дексу k начальное значение к = 1. Тогда получим сумму с первым сла­гаемым: S₁ = S₀ + Y₁ = 0 + Y₁ = Y₁ . Увеличим значение индекса k на единицу: k = k + 1 = 2 и вновь просуммируем со вторым слагаемым по выражению (8.7): S₂ = S₁ + Y₂ = (S₀ + Y₁ ) + Y₂ = (0 + Y₁ ) + Y₂ = Y₁ + Y₂. Вновь увеличим значение индекса k на единицу и просуммируем с третьим членом: S₃ = S₂ + Y₃ = (S₁ + Y₂ ) + Y₃ = (S₀ + Y₁ + Y₂ ) + Y₃ = (0 + Y₁ + Y₂ ) + Y₃ = Y₁ + Y₂ + Y₃ .

Повторяя эти операции до k = n, мы получим искомую сумму

Поскольку при вычислениях надобности в запоминании значений всех слагаемых и промежуточных сумм нет, в качестве S_k и Y_k нужно ис­пользовать простые без индексов переменные и накапливание вести в цикле по формуле

где знак = означает присваивание значения.

Если начальное значение S предварительно приравнять нулю, то после первого выполнения цикла значение S будет равно первому зна­чению функции, находящейся под знаком суммы.

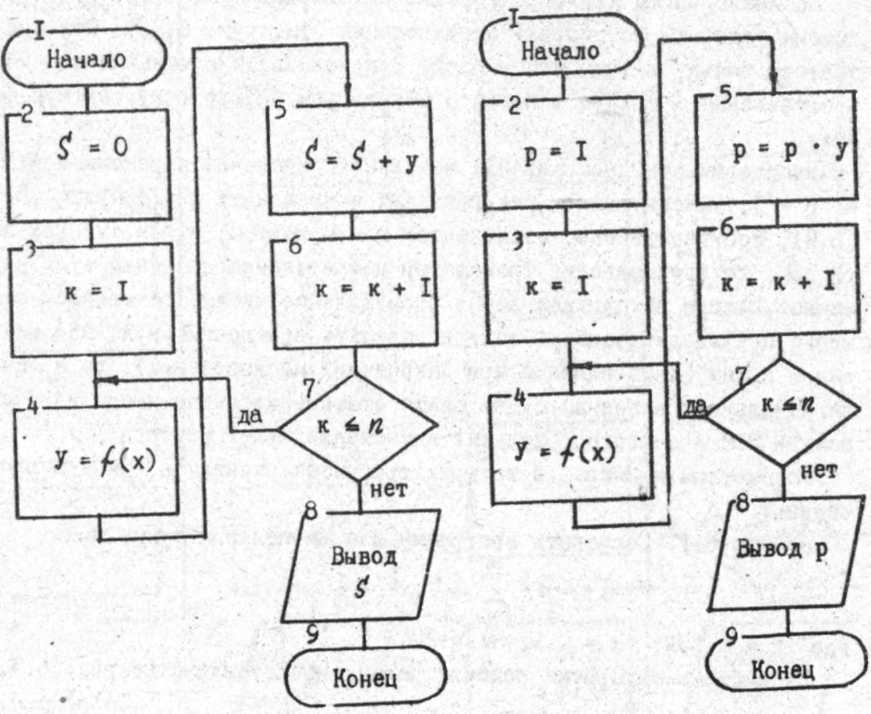
Таким образом, получаем схему, реализующую принцип накапливания суммы. Алгоритм такого принципа включает следующие операции (рис. 8.2,а):

1) присвоение сумме S начального значения: S = 0 (блок 2);

2) присвоение индексу k начального значения: k = 1 (блок 3);

3) вычисление очередного (k-го) слагаемого накапливаемой суммы: (блок 4);

4) накапливание суммы по выражению: S = S + Y_k (блок 5);

5) увеличение значения индекса k на единицу: k = k + 1 (блок 6);

6) проверку текущего значения индекса k с его конечным значением n (блок 7). Если k ≤ n, то возвратимся к п. 3 (блок 4). Если нет (k > n), переходим на следующую операцию (п. 7);

7) выводим на печать полученное значение суммы S (блок 8);

8) останавливаем вычисления (блок 9).

По аналогии с накапливанием суммы принцип вычисления произведений вида (8.6), реализуется при помощи рекуррентной формулы вида

где – произведение, содержащее k-1 сомножитель; – произ­ведение, содержащее k сомножителей; – значение k-го со­множителя.

Использование формулы (8.9) заключается в следующем. Примем на­чальное значение произведения равным единице: р₀ = 1 (при k =1 ). За­дадим индексу k начальное значение k = 1.

Тогда получим произведение с первым сомножителем: P₁ = P₀ * Y₁ = 1 * Y₁ = Y₁ .

Увеличим значение индекса k на единицу: k = k + 1 = 2 и вновь произ­ведем умножение со вторым слагаемым по выражению (8.9): P₂ = P₁ * Y₂ = (P₀ * Y₁ ) * Y₂ = (1 * Y₁ ) * Y₂ = Y₁ *Y₂. Вновь увеличим значение индекса k на единицу и произведем умножение с третьим членом: P₃ = P₂ * Y₃ = (P₁ * Y₂ ) * Y₃ = (P₀ *Y₁ * Y₂ ) * Y₃ = (1 * Y₁ * Y₂ ) * Y₃ = Y₁ * Y₂ * Y₃ .

Рис. 8.2. Блок-схемы алгоритмов вычисления в цикле:

Источник

Программа на Паскале «Вычисление суммы цифр»

Σ Сумма случайных чисел. 🔁 Циклы for, while. Три задачи на нахождение суммы случайно сгенерированных элементов. Для каждой задачи приведено два варианта — классический синтаксис (Turbo/Borland Pascal) и PascalABC.NET

Задачи по информатике и основам программирования на языке Паскаль. В двух решениях используется оператор целочисленного деления, в двух других — используется преобразование числа к строке и цикл for, последнее решение учитывает рекомендации PascalABC.NET.

Программа «Сумма цифр трёхзначного числа»

Program SummaTsifr1;
Var X, Y1, Y2, Y3, Summa : Integer;
begin
writeln(‘Программа вычисления суммы цифр’);
write(‘Введите трёхзначное число X ‘);
readln(X);
Y1 := X div 100;
Y2 := (X — Y1 * 100) div 10;
Y3 := X — Y1 * 100 — Y2 * 10;
Summa := Y1 + Y2 + Y3;
writeln(‘Сумма цифр ‘, Y1:3, Y2:3, Y3:3, ‘ = ‘, Summa: 3)
end.

Замечание:
В процедуре вывода writeln используется форматированный вывод переменной. Например, Y1:3 обозначает, что для вывода значения переменной Y1 будут использоваться три позиции, т.е. в случае однозначного числа, перед ним будет добавлено два пробела, в случае двухзначного числа — добавлен один пробел. При этом если число будет содержать 4 или больше цифр, то оно будет выведено полностью.

Программа «Сумма цифр пятизначного числа»

Program SummaTsifr2;
Var X, Y1, Y2, Y3, Y4, Y5, Summa : Integer;
begin
writeln(‘Программа вычисления суммы цифр ‘);
write(‘Введите пятизначное число X ‘);
readln(X);
Y1 := X div 10000;
Y2 := (X — Y1 * 10000) div 1000;
Y3 := (X — Y1 * 10000 — Y2 * 1000) div 100;
Y4 := (X — Y1 * 10000 — Y2 * 1000 — Y3 * 100) div 10;
Y5 := X — Y1 * 10000 — Y2 * 1000 — Y3 * 100 — Y4 * 10;
Summa := Y1 + Y2 + Y3 + Y4 + Y5;
writeln(‘Сумма цифр ‘, Summa)
end.

Замечание:
В процедуре вывода writeln используется форматированный вывод переменной. Например, Y1:3 обозначает, что для вывода значения переменной Y1 будут использоваться три позиции, т.е. в случае однозначного числа, перед ним будет добавлено два пробела, в случае двухзначного числа — добавлен один пробел. При этом если число будет содержать 4 или больше цифр, то оно будет выведено полностью.

Тема «Использование цикла for». Программа «Сумма цифр числа»

Задание:
Введите число. Найдите сумму цифр. Для решения задачи используйте цикл for и функции работы со строками. Выведите результат на экран.

Program SumNumbers1;
Var
Y : Array[1..20] of Byte; < Массив для сохранения цифр исходного числа >
Xs : String;
Xr, Summa : Real;
J, N, Err : Integer;
begin
writeln(‘Программа вычисления суммы цифр ‘);
write(‘Введите число X (не более 20 цифр)’);
readln(Xr);
Str(Xr, Xs); < Преобразовать число в строку >
N := Length(Xs); < Вычислить длину строки >
for J := 1 to N do Val(Xs[J], Y[J], Err); < Преобразовать каждый символ строки к числу и записать в массив >
Summa := 0;
for J := 1 to N do Summa := Summa + Y[J];
writeln(‘Сумма цифр ‘, Summa)
end.

Замечание:
procedure Str(i: integer; var s: string); Преобразует целое значение i к строковому представлению и записывает результат в s
procedure Val(s: string; var value: byte; var err: integer); Преобразует строковое представление s целого числа к числовому значению и записывает его в переменную value. Если преобразование успешно, то err=0, иначе err>0
function Length(s: string): integer; Возвращает длину строки

Тема «Использование цикла for». Вариант программы «Сумма цифр числа» без использования массива

Задание:
Введите число. Найдите сумму цифр. Для решения задачи используйте цикл for и функции работы со строками. Выведите результат на экран.

Program SumNumbers2;
Var
Y : Byte;
Xs : String;
Xr, Summa : Real;
J, N, Err : Integer;
begin
writeln(‘Программа вычисления суммы цифр ‘);
write(‘Введите число X ‘);
readln(Xr);
Str(Xr, Xs); < Преобразовать число в строку >
N := Length(Xs); < Вычислить длину строки >
Summa := 0;
for J := 1 to N do begin
Val(Xs[J], Y, Err); < Преобразовать каждый символ строки к числу >
Summa := Summa + Y;
end;
writeln(‘Сумма цифр ‘, Summa)
end.

Программа вычисления суммы цифр. Вариант решения на PascalABC.NET

• В программе отсутствуют устаревшие в PascalABC.NET конструкции. В программе используются следующие рекомендованные конструкции PascalABC.NET:
• Используются внутриблочные описания переменных: 6 раз
• Используется инициализация при описании: 3 раза
• Для ввода используется функция вида ReadInteger,ReadReal: 1 раз
• Используется расширенное присваивание: 1 раз
• Для вывода использована Print: 2 раза

(*
Вариант для PascalABC.NET
*)
begin
var Y, Err : Integer;
Var Xs : String;
Println(‘Программа вычисления суммы цифр’);
var Xr := ReadInteger(‘Введите целое число X ‘);
Str(Xr, Xs); < Преобразовать число в строку >
var N := Length(Xs); < Вычислить длину строки >
var Summa : Integer := 0;
for var J := 1 to N do begin
Val(Xs[J], Y, Err); < Преобразовать каждый символ строки к числу >
Summa += Y;
end;
Println(‘Сумма цифр ‘, Summa)
end.

🔁 Использование циклов. Сумма положительных элементов массива. Циклы for, while, repeat. Шесть примеров решения задачи на языке Паскаль. Варианты для Turbo/Borland/FreePascal и PascalABC.NET

Σ Сумма элементов массива. 🔁 Циклы for, while, repeat. Пять примеров решения задачи на языке Паскаль. В некоторых вариантах используется синтаксис для PascalABC.NET

Σ Сумма случайных чисел. 🔁 Циклы for, while. Три задачи на нахождение суммы случайно сгенерированных элементов. Для каждой задачи приведено два варианта — классический синтаксис (Turbo/Borland Pascal) и PascalABC.NET

Источник

9.3.1.4. Алгоритмы вычисления суммы и произведения

При вычислении суммы или произведения ряда чисел пользуются соответствующими формулами.

Сумма равна предыдущей сумме плюс аргумент. Начальная сумма равна нулю. При нахождении количества аргумент равен одному.

Произведение равно предыдущему произведению, умноженному на аргумент. Начальное произведение всегда равно единице.

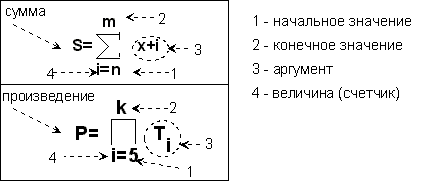
Математически данные формулы записываются так (рис. 9.14).

Если в аргументе около имени какой-нибудь величины стоит индекс счетчика, то внутри цикла необходимо поставить блок ввода этой величины.

Рис. 9. 14. Формулы для вычисления суммы и произведения

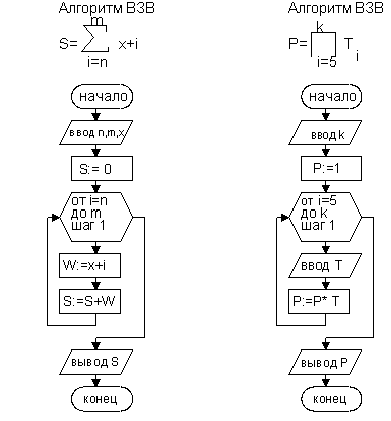
В качестве примера рассмотрим блок-схемы алгоритмов для приведенных на рис. 9.14 примеров.

9.3.1.4. Вложенные циклы

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.

Рис. 9. 15. Блок-схемы алгоритмов вычисления суммы и произведения

При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.

Рассмотрим два примера вычисления вложенных циклов.

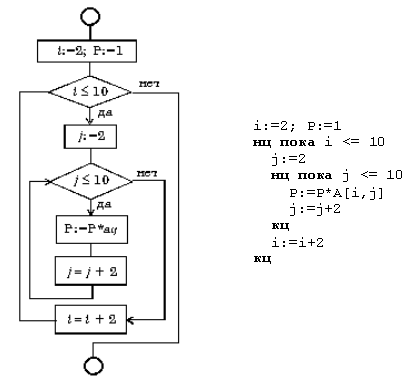
Рис. 9. 16. Вложенный цикл «до»

Вычислите произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов (рис. 9.16).

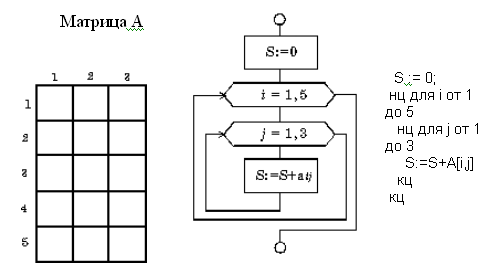
Рис. 9. 17. Вложенный цикл «пока»

Вычислите сумму элементов заданной матрицы А(5,3) – рис. 9.17.

9.4. Языки программирования

9.4.1. Программный способ записи алгоритмов. Уровни языка программирования

При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается некоторый произвол при изображении команд. Вместе с тем такая запись точна настолько, что позволяет человеку понять суть дела и исполнить алгоритм.

Однако на практике в качестве исполнителей алгоритмов используются специальные автоматы — компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на понятном ему языке. И здесь на первый план выдвигается необходимость точной записи команд, не оставляющей места для произвольного толкования их исполнителем.

Следовательно, язык для записи алгоритмов должен быть формализован. Такой язык принято называть языком программирования, а запись алгоритма на этом языке — программой для компьютера.

В настоящее время в мире существует несколько сотен реально используемых языков программирования. Для каждого есть своя область применения.

Любой алгоритм есть последовательность предписаний, выполнив которые можно за конечное число шагов перейти от исходных данных к результату. В зависимости от степени детализации предписаний обычно определяется уровень языка программирования — чем меньше детализация, тем выше уровень языка.

По этому критерию можно выделить следующие уровни языков программирования:

• машинные;
• машинно-оpиентиpованные (ассемблеpы);
• машинно-независимые (языки высокого уровня).

• Процедурные (алгоритмические) (Basic, Pascal, C и др.), которые предназначены для однозначного описания алгоритмов; для решения задачи процедурные языки требуют в той или иной форме явно записать процедуру ее решения.
• Логические (Prolog, Lisp и др.), которые ориентированы не на разработку алгоритма решения задачи, а на систематическое и формализованное описание задачи с тем, чтобы решение следовало из составленного описания.
• Объектно-ориентированные (Object Pascal, C++, Java и др.), в основе которых лежит понятие объекта, сочетающего в себе данные и действия над нами. Программа на объектно-ориентированном языке, решая некоторую задачу, по сути, описывает часть мира, относящуюся к этой задаче. Описание действительности в форме системы взаимодействующих объектов естественнее, чем в форме взаимодействующих процедур.

Источник