Алгоритм флойда уоршелла питон

Saved searches

Use saved searches to filter your results more quickly

You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session. You switched accounts on another tab or window. Reload to refresh your session.

The Floyd-Warshall algorithm for the shortest path problem

Xavier-MaYiMing/Floyd-Warshall-Algorithm

This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.

Name already in use

A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch?

Sign In Required

Please sign in to use Codespaces.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching GitHub Desktop

If nothing happens, download GitHub Desktop and try again.

Launching Xcode

If nothing happens, download Xcode and try again.

Launching Visual Studio Code

Your codespace will open once ready.

There was a problem preparing your codespace, please try again.

Latest commit

Git stats

Files

Failed to load latest commit information.

README.md

Reference: Floyd R W. Algorithm 97: shortest path[J]. Communications of the ACM, 1962, 5(6): 345.

The Floyd-Warshall Algorithm for the shortest path problem

Variables	Meaning
network	Dictionary, , . >
nn	The number of nodes
dis_mat	List, dis_mat[i][j] denotes the length of the shortest path from node i to node j
path_mat	List, path_mat[i][j] denotes the shortest path from node i to node j

if __name__ == '__main__': test_network = < 0: 1: 62, 2: 44, 3: 67>, 1: 0: 62, 2: 32, 4: 52>, 2: 0: 44, 1: 33, 3: 32, 4: 52>, 3: 0: 67, 2: 32, 4: 54>, 4: 1: 52, 2: 52, 3: 54> > print(main(test_network))

< 'path': [ [[0], [0, 1], [0, 2], [0, 3], [0, 2, 4]], [[1, 0], [1], [1, 2], [1, 2, 3], [1, 4]], [[2, 0], [2, 1], [2], [2, 3], [2, 4]], [[3, 0], [3, 2, 1], [3, 2], [3], [3, 4]], [[4, 2, 0], [4, 1], [4, 2], [4, 3], [4]] ], 'length': [ [0, 62, 44, 67, 88], [62, 0, 32, 65, 52], [44, 33, 0, 32, 52], [67, 64, 32, 0, 54], [104, 52, 52, 54, 0] ] >

About

The Floyd-Warshall algorithm for the shortest path problem

Источник

Floyd-Warshall algorithm

Floyd-Warshall algorithm is an algorithm for finding the shortest path between all the pairs of vertices in a weighted graph. The result of the algorithm is a list of lengths of shortest paths between all pairs of vertices.

The algorithm was first designed as an example for dynamic programming by Robert Floyd in 1962. The same year, Stephen Warshall published essentially the same algorithm, but as a graph example. As the algorithms were essentially the same, the algorithm got named after both authors.

How does it work?​

Floyd-Warshall algorithm creates a series of matrices with dimension n x n, where n is the number of nodes in the graph. Elements of the matrices are filled with distances from node i to node j. If there is no path between the two nodes, the element is put as infinity.

Each next matrix takes into account the node that is intermediate between the source node and the target node. Element of the matrix is filled if the sum of distance from source node to intermediate node and distance from intermediate node to target node is lower than the current distance. The algorithm is repeated as many times as there’s nodes in the graph.

The resulting matrix contains the length of the shortest path between each pair of nodes.

The difference from other shortest path algorithms​

Floyd-Warshall algorithm can find lengths of the shortest paths between all pairs of vertices in a graph. The algorithm works with both directed and undirected graphs. It accepts both positive and negative values as weights.

Floyd-Warshall algorithm is used in solving many different problems such as finding the shortest path in a directed graph, finding the transitive closure of directed graphs, finding the inversion of real matrices, testing whether an undirected graph is a bipartite and fast computation of pathfinder networks.

Pseudocode​

dist = |V| x |V| FOR EACH edge (u,v)  dist[u][v] = weight(u,v) ENDFOR FOR EACH vertex v  dist[u][v] = 0 ENDFOR FOR k = 1 to |V|  FOR i = 1 to |V|  FOR j from 1 to |V|  IF dist[i][j] > dist[i][k] + dist[k][j] THEN  Dist[i][j] = dist[i][k] + dist[k][j]  ENDIF  ENDFOR  ENDFOR ENDFOR 

Usage in NetworkX​

Not fast enough? Find 100x faster algorithms here.

Method input​

The first input parameter of the method, G, is a NetworkX graph. The fifth parameter, weight, represents the edge attribute that should be used as the edge weight. If it’s not specified, the default value is ‘weight’.

Method output​

The output of the method is a dictionary keyed by source and target, of shortest paths distances between nodes..

Example​

import networkx as nx import pprint as pp edges = [(1,2, 'weight':4>), (1,3,'weight':2>), (2,3,'weight':1>), (2,4, 'weight':5>), (3,4, 'weight':8>), (3,5, 'weight':10>), (4,5,'weight':2>), (4,6,'weight':8>), (5,6,'weight':5>)] edge_labels = (1,2):4, (1,3):2, (2,3):1, (2,4):5, (3,4):8, (3,5):10, (4,5):2, (4,6):8, (5,6):5>  G = nx.Graph() for i in range(1,7):  G.add_node(i) G.add_edges_from(edges) pos = nx.planar_layout(G) nx.draw(G, pos, with_labels = True) nx.draw_networkx_edge_labels(G, pos,edge_labels=edge_labels) fw = nx.floyd_warshall(G, weight='weight') results = a:dict(b) for a,b in fw.items()> pp.pprint(results) 

Источник

Floyd Warshall Algorithm (Python) | Dynamic Programming

In this article, we will study what is Floyd Warshall Algorithm in the field of Dynamic Programming. We will also study the example and the python code with its corresponding output to learn and understand the algorithm. At last, we will go through the practical real-world application of the Floyd Warshall Algorithm.

What is Floyd Warshall Algorithm?

Just like Dijkstra’s algorithm, the Floyd Warshall algorithm is used to find the shortest path between all vertices in the weighted graph. This algorithm works with both directed and undirected graphs but it does not work along with the graph with negative cycles. Therefore, if the distance from the vertex v from itself is negative then we can assume that the graph has the presence of a negative cycle. This algorithm follows the dynamic programming approach as its working pattern. Here the algorithm doesn’t construct the path itself but it can reconstruct the path with a simple modification. Floyd Warshall algorithm is also known as Roy Warshall algorithm or Roy-Floyd algorithm. Let us study the working of the Floyd Warshall algorithm.

Algorithm

We construct a matrix D that gives the length of the shortest path between each pair of nodes.

The algorithm initializes D to L, that is, to the direct distances between nodes. It then does n iterations, after iteration k, D gives the length of the shortest paths that only use nodes in as intermediate nodes.

After n iterations, D, therefore, gives the length of shortest paths using any of the nodes in N as an intermediate node. If D_k represents the matrix D after k th iteration it can be implemented by

We use the principle of optimality to compute length from i to j passing through k.

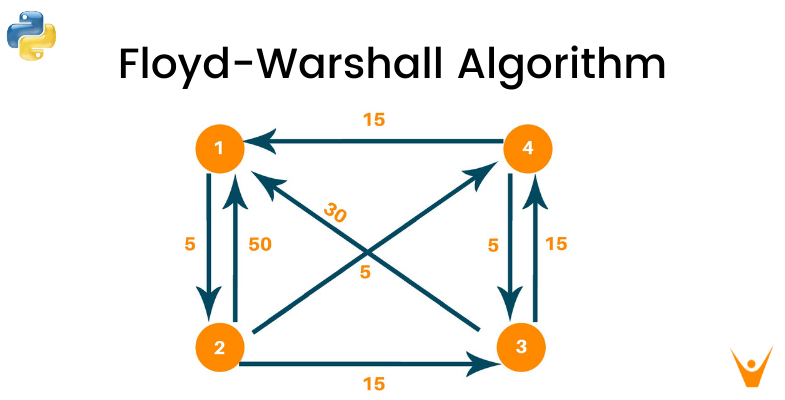
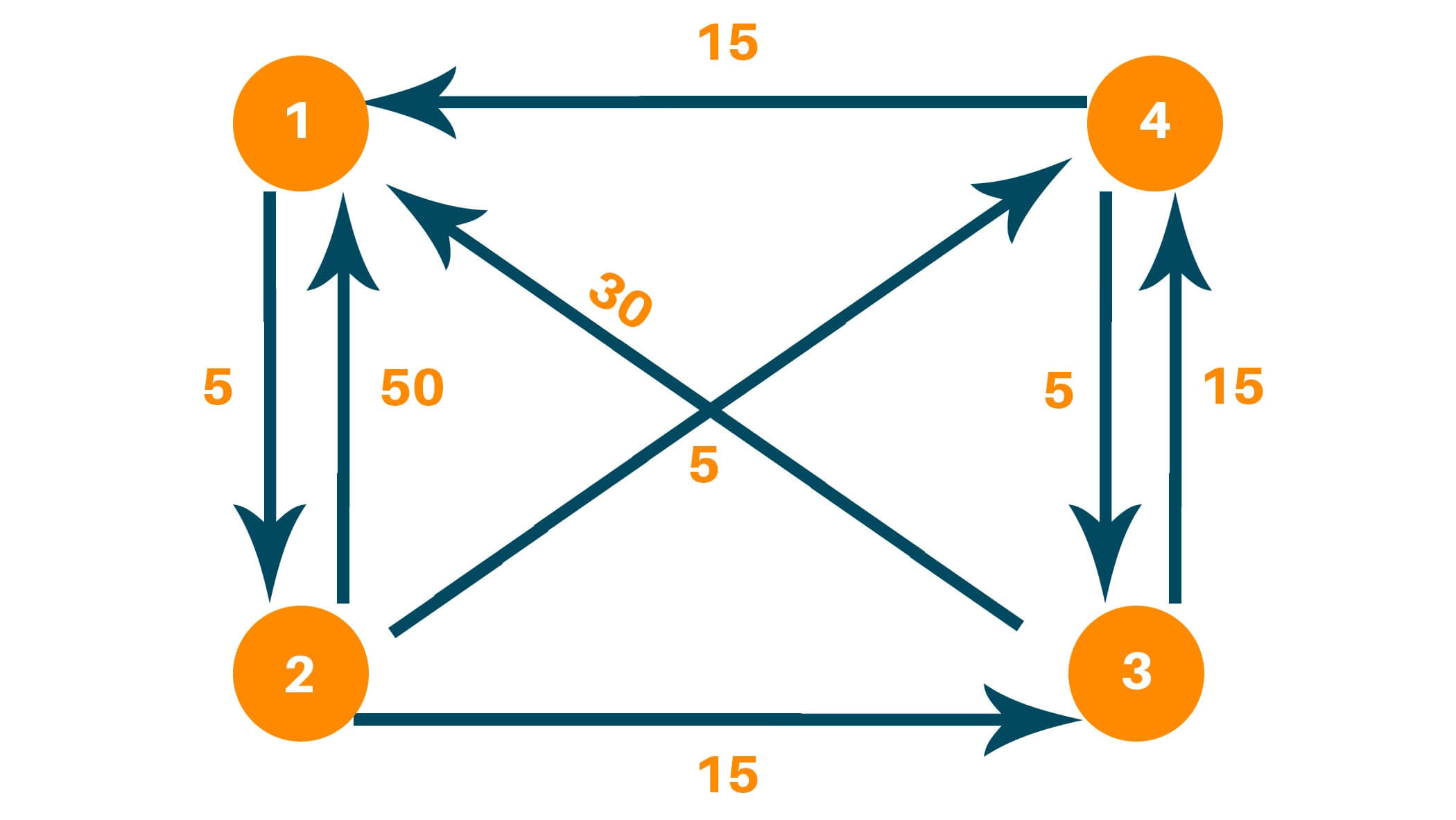
How Floyd Warshall Algorithm Works (Example)

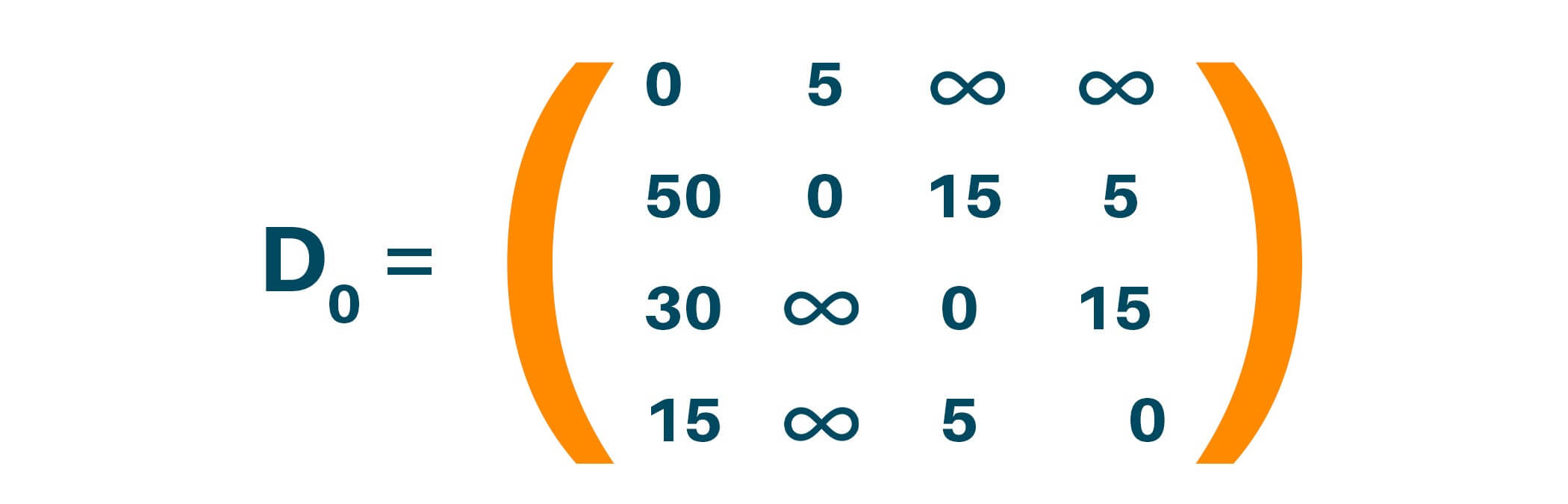
Creating matrix D₀ contains the distance between each node with ‘0’ as an intermediate node.

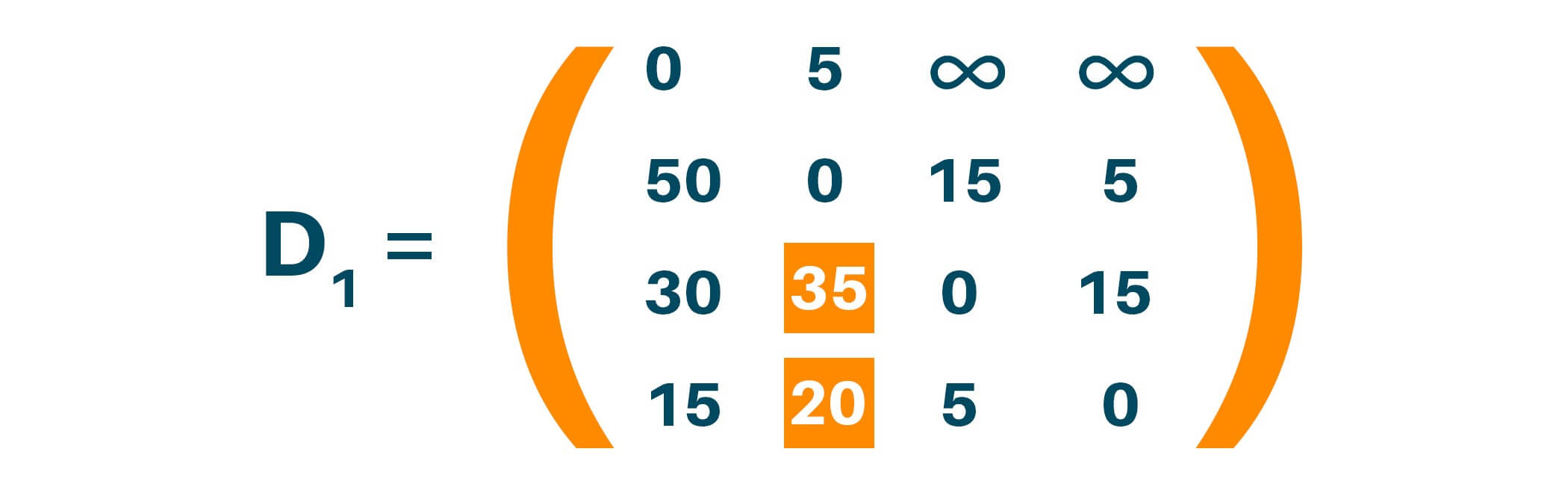
Updating matrix D₁ which contains the distance between each node with ‘1’ as an intermediate node. Update distance if minimum distance value smaller than existing distance value found.

Here distance (3, 2) is updated from infinity to 35, and distance (4, 2) is updated from infinity to 20 as shown below.

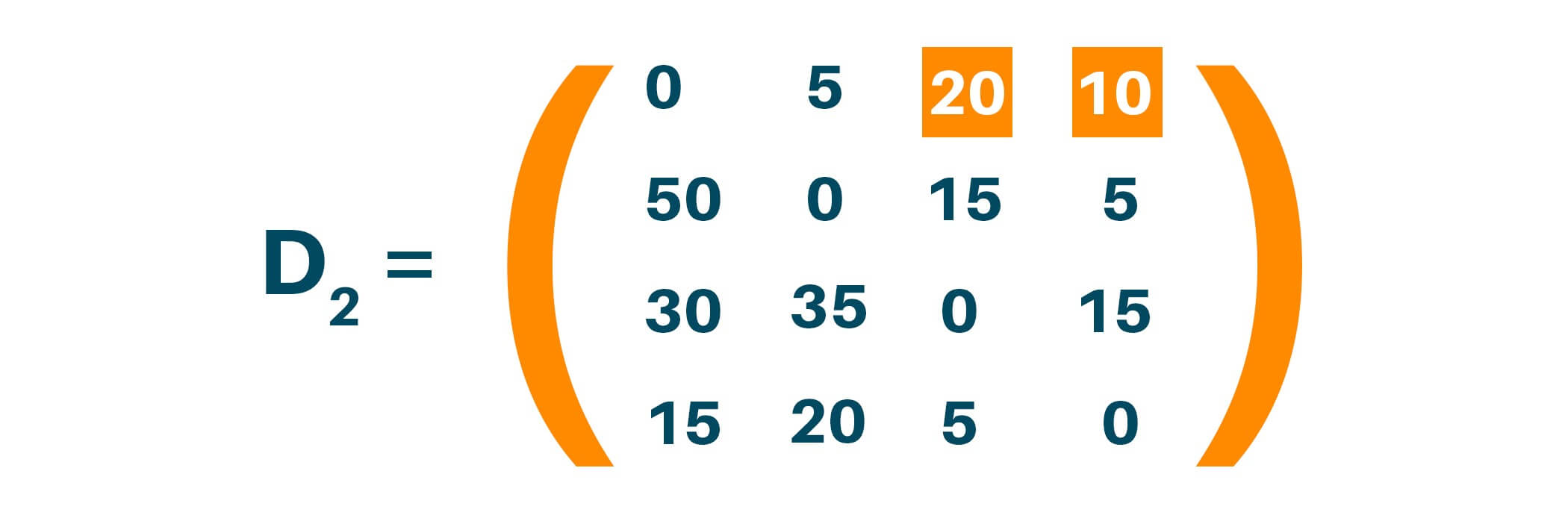
Updating matrix D₂ contains the distance between two nodes with ‘2’ as an intermediate node.

Update distance if minimum distance value smaller than existing distance value found. Here distance (1, 3) is updated from infinity to 20, and distance (1, 4) is updated from infinity to 10.

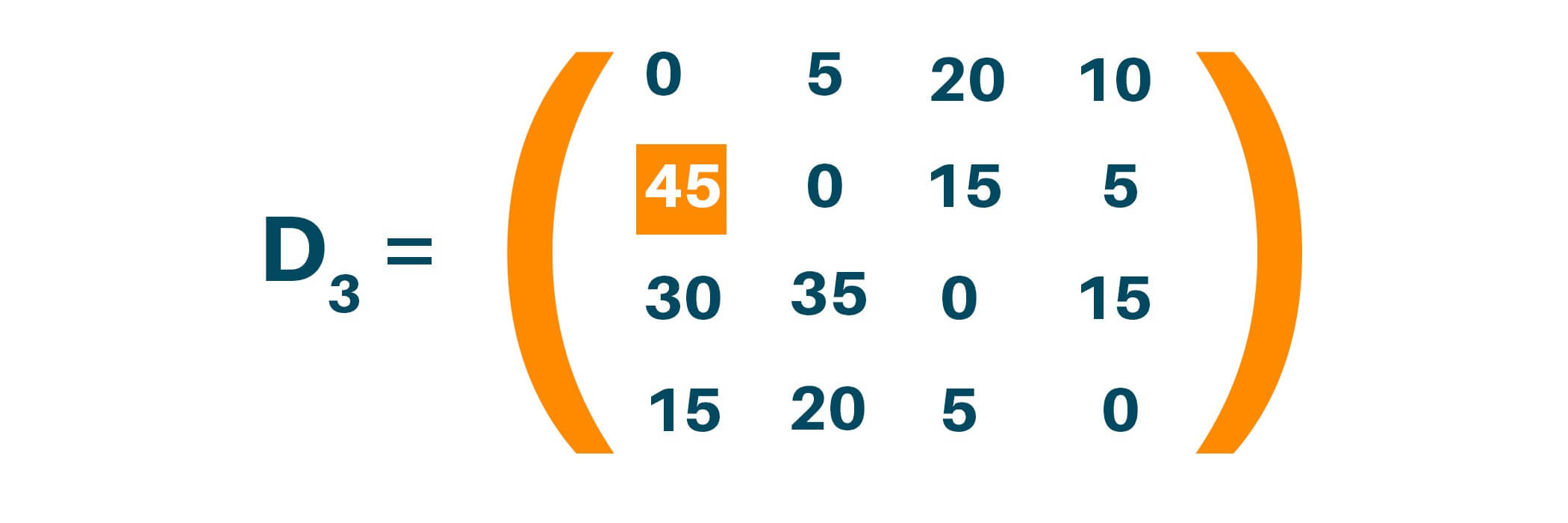
Updating matrix D₃ contains the distance between two nodes with ‘3’ as an intermediate node.

Update distance if minimum distance value smaller than existing distance value found. Here distance (2, 1) is updated from 50 to 45

Updating matrix D₄ contains the distance between two nodes with ‘4’ as an intermediate node. Update distance if minimum distance value smaller than existing distance value found.

Here distance (1, 3) is updated from 20 to 15; distance (2, 1) is updated from 45 to 20, and distance (2, 3) is updated from 15 to 10

Python Code for Floyd Warshall Algorithm

# Number of vertices nV = 4 INF = 999 # Algorithm def floyd(G): dist = list(map(lambda p: list(map(lambda q: q, p)), G)) # Adding vertices individually for r in range(nV): for p in range(nV): for q in range(nV): dist[p][q] = min(dist[p][q], dist[p][r] + dist[r][q]) sol(dist) # Printing the output def sol(dist): for p in range(nV): for q in range(nV): if(dist[p][q] == INF): print("INF", end=" ") else: print(dist[p][q], end=" ") print(" ") G = [[0, 5, INF, INF], [50, 0, 15, 5], [30, INF, 0, 15], [15, INF, 5, 0]] floyd(G)

Time Complexity

There are three loops for computing the shortest path in the graph and each of these loops has constant complexities. Therefore, due to this, the time complexity of the Floyd Warshall algorithm is O(n 3 ). Also, the space complexity of the Floyd Warshall algorithm is O(n 2 ).

Application of Floyd Warshall Algorithm

• Floyd Warshall Algorithm helps to find the inversion of real matrices
• It helps in testing whether the undirected graph is bipartite
• It helps to find the shortest path in a directed graph
• Different versions of the Floyd Warshall algorithm help to find the transitive closure of a directed graph
• This algorithm helps to find the regular expression the are accepted by finite automata.
• It helps in finding the similarity between the graphs
• Floyd Warshall algorithm helps in finding the optimal routing i.e the maximum flow between two vertices

Conclusion

Therefore, in the above article, we studied what is Floyd Warshall algorithm and how it is different from Dijkstra’s algorithm for finding the shortest path between all vertices in a weighted graph. We studied the algorithm for Floyd Warshall along with the example explaining the algorithm in detail. We learned the python code with its corresponding output and the time complexity to run the algorithm on any weighted graph. Lastly, we understood the application of the Floyd Warshall algorithm which can help us to apply it in real life.

Источник