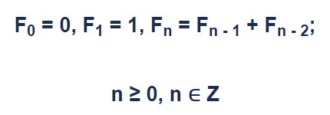Алгоритм числа фибоначчи java

Fibonacci Series in Java

Repeatedly, code that works in dev breaks down in production. Java performance issues are difficult to track down or predict.

Simply put, Digma provides immediate code feedback. As an IDE plugin, it identifies issues with your code as it is currently running in test and prod.

The feedback is available from the minute you are writing it.

Imagine being alerted to any regression or code smell as you’re running and debugging locally. Also, identifying weak spots that need attending to, based on integration testing results.

Of course, Digma is free for developers.

As always, the writeup is super practical and based on a simple application that can work with documents with a mix of encrypted and unencrypted fields.

We rely on other people’s code in our own work. Every day.

It might be the language you’re writing in, the framework you’re building on, or some esoteric piece of software that does one thing so well you never found the need to implement it yourself.

The problem is, of course, when things fall apart in production — debugging the implementation of a 3rd party library you have no intimate knowledge of is, to say the least, tricky.

Lightrun is a new kind of debugger.

It’s one geared specifically towards real-life production environments. Using Lightrun, you can drill down into running applications, including 3rd party dependencies, with real-time logs, snapshots, and metrics.

Learn more in this quick, 5-minute Lightrun tutorial:

Slow MySQL query performance is all too common. Of course it is. A good way to go is, naturally, a dedicated profiler that actually understands the ins and outs of MySQL.

The Jet Profiler was built for MySQL only, so it can do things like real-time query performance, focus on most used tables or most frequent queries, quickly identify performance issues and basically help you optimize your queries.

Critically, it has very minimal impact on your server’s performance, with most of the profiling work done separately — so it needs no server changes, agents or separate services.

Basically, you install the desktop application, connect to your MySQL server, hit the record button, and you’ll have results within minutes:

DbSchema is a super-flexible database designer, which can take you from designing the DB with your team all the way to safely deploying the schema.

The way it does all of that is by using a design model, a database-independent image of the schema, which can be shared in a team using GIT and compared or deployed on to any database.

And, of course, it can be heavily visual, allowing you to interact with the database using diagrams, visually compose queries, explore the data, generate random data, import data or build HTML5 database reports.

Get started with Spring 5 and Spring Boot 2, through the Learn Spring course:

1. Overview

In this tutorial, we’ll look at the Fibonacci series.

Specifically, we’ll implement three ways to calculate the n th term of the Fibonacci series, the last one being a constant-time solution.

2. Fibonacci Series

The Fibonacci series is a series of numbers in which each term is the sum of the two preceding terms. It’s first two terms are 0 and 1.

For example, the first 11 terms of the series are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and 55.

In mathematical terms, the sequence S_n of the Fibonacci numbers is defined by the recurrence relation:

S(n) = S(n-1) + S(n-2), with S(0) = 0 and S(1) = 1

Now, let’s look at how to calculate the n th term of the Fibonacci series. The three methods we’ll be focusing on are recursive, iterative, and using Binet’s formula.

2.1. Recursive Method

For our first solution, let’s simply express the recurrence relation directly in Java:

public static int nthFibonacciTerm(int n) < if (n == 1 || n == 0) < return n; >return nthFibonacciTerm(n-1) + nthFibonacciTerm(n-2); >

As we can see, we check whether n is equal to 0 or 1. If it true, then we return that value. In any other case, we recursively call the function to calculate the (n-1) th term and (n-2) th term and return their sum.

Although the recursive method is simple to implement, we see that this method does a lot of repeated calculations. For instance, in order to calculate the 6th term, we make calls to calculate the 5th and the 4th term. Moreover, the call to calculate the 5th term makes a call to calculate the 4th term again. Because of this fact, the recursive method does a lot of redundant work.

As it turns out, this makes its time complexity exponential; O(Φ n ) to be exact.

2.2. Iterative Method

In the iterative method, we can avoid the repeated calculations done in the recursive method. Instead, we calculate the terms of the series and store the previous two terms to calculate the next.

Let’s take a look at its implementation:

public static int nthFibonacciTerm(int n) < if(n == 0 || n == 1) < return n; >int n0 = 0, n1 = 1; int tempNthTerm; for (int i = 2; i return n1; >

Firstly, we check whether the term to be calculated is the 0 th term or 1 st term. If that is the case, we return the initial values. Otherwise, we compute the 2 nd term using n0 and n1. Then, we modify the values of n0 and n1 variables to store the 1 st term and 2 nd term respectively. We keep on iterating until we have calculated the required term.

The iterative method avoids repetitive work by storing the last two Fibonacci terms in variables. The time complexity and space complexity of the iterative method is O(n) and O(1) respectively.

2.3. Binet’s Formula

We have only defined the n th Fibonacci number in terms of the two before it. Now, we will look at Binet’s formula to calculate the n th Fibonacci number in constant time.

The Fibonacci terms maintain a ratio called golden ratio denoted by Φ, the Greek character pronounced ‘phi’.

First, let’s look at how the golden ratio is calculated:

Now, let’s look at Binet’s formula:

Actually, this means that we should be able to get the n th Fibonacci number with just some arithmetic.

Let’s express this in Java:

public static int nthFibonacciTerm(int n) < double squareRootOf5 = Math.sqrt(5); double phi = (1 + squareRootOf5)/2; int nthTerm = (int) ((Math.pow(phi, n) - Math.pow(-phi, -n))/squareRootOf5); return nthTerm; >

We first calculate the squareRootof5 and phi and store them in variables. Later, we apply Binet’s formula to get the required term.

Since we’re dealing with irrational numbers here, we’ll only get an approximation. Consequently, we’ll need to hold onto more decimal places for higher Fibonacci numbers to account for round-off error.

We see that the above method calculates the n th Fibonacci term in constant time, or O(1).

3. Conclusion

In this brief article, we looked at the Fibonacci series. We looked at a recursive and an iterative solution. Then, we applied Binet’s formula to create a constant-time solution.

As always, the full source code of the working examples is available over on GitHub.

Slow MySQL query performance is all too common. Of course it is. A good way to go is, naturally, a dedicated profiler that actually understands the ins and outs of MySQL.

The Jet Profiler was built for MySQL only, so it can do things like real-time query performance, focus on most used tables or most frequent queries, quickly identify performance issues and basically help you optimize your queries.

Critically, it has very minimal impact on your server’s performance, with most of the profiling work done separately — so it needs no server changes, agents or separate services.

Basically, you install the desktop application, connect to your MySQL server, hit the record button, and you’ll have results within minutes:

Источник

Вычисление чисел Фибоначчи

Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.

Формула записывается следующим образом:

Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.

Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.

Вычислить ряд Фибоначчи циклом

Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:

Тогда наша последовательность будет иметь такой вид:

Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:

Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.

Найти число Фибоначчи через рекурсию

Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.

Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.

Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:

public int fibonacciValue(num) < if (num else if (num == 2) < return 1; >else < return fibonacciValue(num - 1) + fibonacciValue(num - 2); >>

Если в качестве num задать большое значение, программа зависнет.

Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.

Использовать для вычисления Stream

Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.

И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:

Stream.iterate(new int[], arr -> new int[]) //Задаём лимит значений: .limit(num) //Отбираем по первому элементу каждого массива: .map(y -> y[0]) //Выводим в консоль: .forEach(x -> System.out.println(x));

В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr . В консоль будет выведено следующее:

А так мы получим сумму чисел последовательности по элемент num включительно:

int fibonacciValuesSum = Stream.iterate(new int[], arr -> new int[]) .limit(num) .map(y -> y[0]) .mapToInt(Integer::intValue) .sum(); System.out.println(fibonacciValuesSum);

Математический тест

Любите математику? Попробуйте решить наш математический тест:

Источник