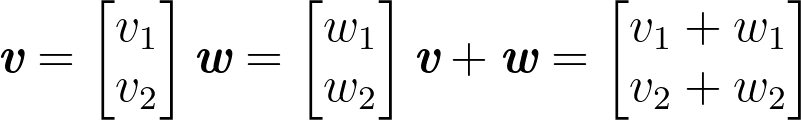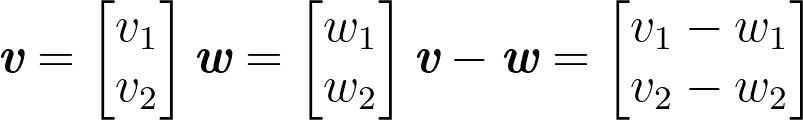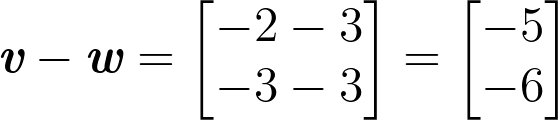Adding vectors in python

Работа с векторами в Python с помощью NumPy

В этом уроке мы узнаем, как создать вектор с помощью библиотеки Numpy в Python. Мы также рассмотрим основные операции с векторами, такие как сложение, вычитание, деление и умножение двух векторов, векторное точечное произведение и векторное скалярное произведение.

Что такое вектор в Python?

Вектор известен как одномерный массив. Вектор в Python – это единственный одномерный массив списков, который ведет себя так же, как список Python. Согласно Google, вектор представляет направление, а также величину; особенно он определяет положение одной точки в пространстве относительно другой.

Векторы очень важны в машинном обучении, потому что у них есть величина, а также особенности направления. Давайте разберемся, как мы можем создать вектор на Python.

Создание вектора в Python

Модуль Python Numpy предоставляет метод numpy.array(), который создает одномерный массив, то есть вектор. Вектор может быть горизонтальным или вертикальным.

Вышеупомянутый метод принимает список в качестве аргумента и возвращает numpy.ndarray.

Давайте разберемся в следующих примерах.

Пример – 1: горизонтальный вектор

# Importing numpy import numpy as np # creating list list1 = [10, 20, 30, 40, 50] # Creating 1-D Horizontal Array vtr = np.array(list1) vtr = np.array(list1) print("We create a vector from a list:") print(vtr)

We create a vector from a list: [10 20 30 40 50]

Пример – 2: Вертикальный вектор

# Importing numpy import numpy as np # defining list list1 = [[12], [40], [6], [10]] # Creating 1-D Vertical Array vtr = np.array(list1) vtr = np.array(list1) print("We create a vector from a list:") print(vtr)

We create a vector from a list: [[12] [40] [ 6] [10]]

Базовые операции вектора Python

После создания вектора мы теперь будем выполнять арифметические операции над векторами.

Ниже приведен список основных операций, которые мы можем производить с векторами:

• сложение;
• вычитание;
• умножение;
• деление;
• точечное произведение;
• скалярные умножения.

Сложение двух векторов

В векторном сложении это происходит поэлементно, что означает, что сложение будет происходить поэлементно, а длина будет такой же, как у двух аддитивных векторов.

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [11,12,13,14,15] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create vector from a list 2:") print(vtr2) vctr_add = vctr1+vctr2 print("Addition of two vectors: ",vtr_add)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [11 12 13 14 15] Addition of two vectors: [21 32 43 54 65]

Вычитание

Вычитание векторов выполняется так же, как и сложение, оно следует поэлементному подходу, и элементы вектора 2 будут вычтены из вектора 1. Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_sub = vtr1-vtr2 print("Subtraction of two vectors: ",vtr_sub)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Subtraction of two vectors: [5 18 26 37 49]

Умножение векторов

Элементы вектора 1 умножаются на вектор 2 и возвращают векторы той же длины, что и векторы умножения.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_mul = vtr1*vtr2 print("Multiplication of two vectors: ",vtr_mul)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Multiplication of two vectors: [ 50 40 120 120 50]

Умножение производится следующим образом.

vct[0] = x[0] * y[0] vct[1] = x[1] * y[1]

Первый элемент вектора 1 умножается на первый элемент соответствующего вектора 2 и так далее.

Операция деления двух векторов

В операции деления результирующий вектор содержит значение частного, полученное при делении двух элементов вектора.

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_div = vtr1/vtr2 print("Division of two vectors: ",vtr_div)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Division of two vectors: [ 2. 10. 7.5 13.33333333 50. ]

Как видно из вышеприведенного вывода, операция деления вернула частное значение элементов.

Векторное точечное произведение

Векторное скалярное произведение выполняется между двумя последовательными векторами одинаковой длины и возвращает единичное скалярное произведение. Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.

vector c = x . y =(x1 * y1 + x2 * y2)

Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_product = vtr1.dot(vtr2) print("Dot product of two vectors: ",vtr_product)

We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Dot product of two vectors: 380

Векторно-скалярное умножение

В операции скалярного умножения; мы умножаем скаляр на каждую компоненту вектора. Давайте разберемся в следующем примере.

import numpy as np list1 = [10,20,30,40,50] vtr1 = np.array(list1) scalar_value = 5 print("We create vector from a list 1:") print(vtr1) # printing scalar value print("Scalar Value : " + str(scalar_value)) vtr_scalar = vtr1 * scalar_value print("Multiplication of two vectors: ",vtr_scalar)

We create vector from a list 1: [10 20 30 40 50] Scalar Value : 5 Multiplication of two vectors: [ 50 100 150 200 250]

В приведенном выше коде скалярное значение умножается на каждый элемент вектора в порядке s * v =(s * v1, s * v2, s * v3).

Источник

Add and Subtract Vectors In Python

Recall that a vector in math is a quantity that describes movement from one point to another. A vector quantity has both magnitude and direction . Check out our previous tutorial on how to plot vectors on graphs in Python.

Let’s start with 2D vector addition. See the general formula below:

Vector Addition

To add vector v and w we simply add the first component of each vector (v₁ and w₁) which gives us the first component of the sum (v₁ + w₁). Then we add the second component of each vector (v₂ and w₂) which gives us the second component of the sum (v₂ + w₂). Our result is a column vector with the same amount of rows and columns as each of the vectors that comprise the sum (a column vector with 2 rows and 1 column in this case).

It’s really that simple. Let’s write some code to add 2 2D vectors:

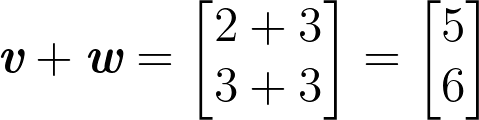
Above we give two examples using numpy arrays. Using numpy gives us the result that we expect in both cases. Example 1 is evaluated as follows:

Example 1

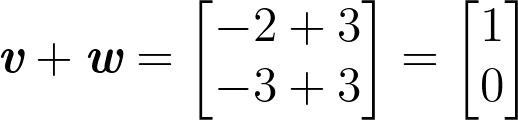
Example 2 is evaluated as follows:

Example 2

Generally speaking adding vectors abides by the commutative law which means:

Adding Vectors is Commutative

Let’s do some 2D vector subtraction. The same principle applies but this time we are subtracting the first and second components which means (v₁ – w₁) and (v₂ – w₂) respectively. This gives us the two components of the result vector:

Vector Subtraction

Note that vector subtraction is not commutative. Now let’s write some code:

Example 3 is evaluated as follows:

Example 3

Example 4 is evaluated as follows:

Example 4

Now let’s do another example, but this time let’s plot our examples on a graph. First, let’s show how we evaluate the examples:

v-w

Here’s the code that will evaluate our vector arithmetic and plot them on a graph:

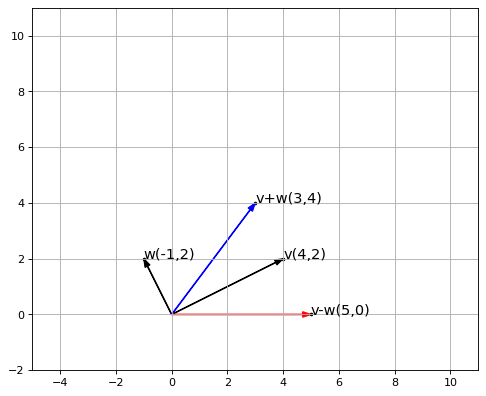
(,)', (vector2d[0],vector2d[1]),fontsize=13) plt.scatter(vector2d[0],vector2d[1], s=5,c='black') return plt.arrow(origin[0], origin[1], vector2d[0], vector2d[1], head_width=0.2, head_length=0.3, length_includes_head=True, width=0.02, **options) figure(figsize=(8, 6), dpi=80) v = np.array([4,2]) w = np.array([-1,2]) vw = v+w plot_vector2d(v,'v', color='black') #v plot_vector2d(w,'w', color='black') #w plot_vector2d(vw, 'v+w', color='b') #v+w vw = v-w plot_vector2d(vw, 'v-w', color='r') #v-w plt.axis([-5, 11, -2, 11]) plt.grid() plt.gca().set_aspect("equal") plt.show()

Let’s explain what’s going on here:

1. We import the numpy and matplotlib libraries which we will use.
2. We define a function plot_vector2d which accepts a numpy vector (and a few other parameters) and adds them to a vector plot. The plot shows each vector as an arrow that starts at the origin and terminates at the vector point (represented by a small dot at the end of each arrowhead) on the Cartesian plane. Each vector point is also labelled for readability.
3. We define vectors v and w. We plot the vectors individually, the sum of the vectors (v+w) and the difference of the vectors (v-w) on the same plot.
4. We set the scale of the x-axis and y-axis.
5. We show the plot to the user on a square grid graph.

The above code will give us the following plot:

Plot Showing Vector Addition and Subtraction

So we know how to add and subtract vectors in Python and also plot them on a cartesian plane. Next we will be doing vector multiplication. Find the Python Notebook for this tutorial HERE. Find the full code HERE.

Источник